
- •8) Метод деления пополам
- •9) Метод хорд
- •10) Метод касательных
- •11) Метод простых итерации.
- •12) Комбинированный метод
- •13) Метод Гаусса
- •14) Метод Жордана-Гаусса
- •15) Метод Якоби
- •17) Метод Зейделя
- •18) Метод исключения Гаусса. Вычисление определителя методом исключения
- •19) Метод простых итераций для снлау
- •21) Постановка задачи интерполяции.
- •22) Линейная интерполяция
- •23) Квадратичная интерполяция
- •24) Формула Лагранжа
- •26) Метод наименьших квадратов
- •27) Непрерывное приближение
- •28) Подбор эмпирических формул
- •1. Линейная зависимость
- •2.Степенная зависимость
- •3 Показательная зависимость
- •5. Логарифмическая функция
- •30) Численное дифференцирование. Метод аппроксимации конечными разностями.
- •31) Численное дифференцирование с использованием формулы Лагранжа
- •32) Численное интегрирование. Метод прямоугольников.
- •33) Численное интегрирование. Метод трапеций.
- •34) Численное интегрирование. Формула Симпсона.
- •35) Задача Коши для дифференциального уравнения
- •36) Метод Эйлера
- •37) Метод Рунге-Кута
- •38) Метод Адамса
17) Метод Зейделя
Дана система линейных уравнений
![]() ,
(1)
,
(1)
где ![]() -квадратная
невырожденная матрица.
-квадратная
невырожденная матрица.
Представив A в виде суммы
двух матриц ![]() ,
где
,
где ![]()
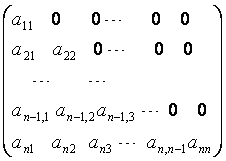 ;
;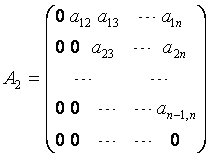 ,
запишем (1) в виде:
,
запишем (1) в виде:
![]() (1a)
(1a)
Уравнение (1a) преобразуем в реккурентную формулу метода Зейделя:
![]() ,
k =
0,1,2,…
(2)
,
k =
0,1,2,…
(2)
Вычитая из обеих частей (2) ![]() ,
получим представление (2) в виде:
,
получим представление (2) в виде:
![]() , k =
0,1,2,… (2a)
, k =
0,1,2,… (2a)
Обозначив ![]() ,
, ![]() ,
получим расчетные формулы метода
Зейделя в матричном виде:
,
получим расчетные формулы метода
Зейделя в матричном виде:
![]() ;
; ![]() ,
, ![]() 0,
1, ... (3).
0,
1, ... (3).
Из (2) можно получить расчетные формулы
для ![]() в
координатной форме:
в
координатной форме:
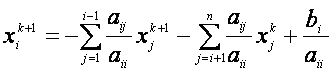 ,
, ![]() 1,
..., n,
1,
..., n, ![]() 0,
1, ... . (4)
0,
1, ... . (4)
Таким образом, метод Зейделя отличается
от метода Якоби тем, что, найдя ![]() ,
его сразу используют для вычисления
,
его сразу используют для вычисления ![]() (по
начальным
(по
начальным ![]() ,
, ![]() ,
...,
,
..., ![]() находят
находят ![]() ,
затем, используя
,
затем, используя ![]() ,
, ![]() ,
...,
,
находят
,
...,
,
находят ![]() и
т.д.).
и
т.д.).
В качестве ![]() можно
взять любой, например, нулевой вектор.
Критерий остановки расчетов:
можно
взять любой, например, нулевой вектор.
Критерий остановки расчетов: ![]() .
Условием сходимости метода Зейделя
является
.
Условием сходимости метода Зейделя
является
![]() (5).
(5).
18) Метод исключения Гаусса. Вычисление определителя методом исключения
Пусть дана матрица

Приведем матрицу к верхней треугольной. Вычтем из второй строки первую, умноженную на такое число, при котором первый элемент второй строки обратится в нуль. То же проделаем со всеми остальными строками. В результате все элементы первого столбца, лежащие ниже главной диагонали, обратятся в нуль. Затем, используя вторую строку, обратим в нуль соответствующие элементы второго столбца. Последовательно продолжая этот процесс, приведем матрицу систему к верхней треугольной форме.
Запишем общие формулы метода Гаусса. Пусть проведено исключение к элементов из (k-1)-го столбца. Тогда останутся строки с ненулевыми элементами ниже главной диагонали.
Умножим k-ю строку на число
![]()
![]() m
> k (3)
m
> k (3)
и вычтем из m-й строки. Первый ненулевой элемент этой строки обратится в нуль, а остальные изменятся по формулам
(![]() 4)
4)
![]() k
< m(5)
k
< m(5)
Проведя вычисления по этим формулам при всех указанных индексах, обратим в нуль элементы k-го столбца, лежащие ниже главной диагонали. Аналогичная процедура приводит матрицу системы к верхней треугольной форме, при этом весь процесс приведения называется прямым ходом метода Гаусса.
Определитель треугольной матрицы равен произведению диагональных элементов. В результате выполнения прямого хода метода исключения система линейных уравнений приводится к верхней треугольной матрице. Следовательно, определитель матрицы системы может быть вычислен как произведение диагональных элементов:
 (6)
(6)
19) Метод простых итераций для снлау
Запишем систему нелинейных уравнений в виде
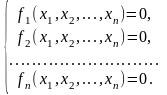 (1)
или коротко в виде
(1)
или коротко в виде
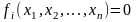 ,
где
.
,
где
.
Точное решение системы (1) обозначим
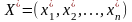 (2)
(2)
Для того, чтобы систему (1) решить методом простой итерации, во-первых, преобразуем её к виду
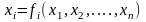 ,
где
.
,
где
.
Функции, стоящие справа в (3) обладают
теми же свойствами, что и функции в
(1).Во-вторых, в области D
выберем любую точку
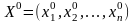 и назовём её нулевым приближением к
точному решению системы (3). В-третьих,
координаты точки
и назовём её нулевым приближением к
точному решению системы (3). В-третьих,
координаты точки
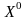 подставим
в правую часть системы (3) и вычислим
значения величин, стоящих слева в этой
системе.
подставим
в правую часть системы (3) и вычислим
значения величин, стоящих слева в этой
системе.
или коротко
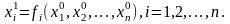
Величины
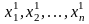 ,
стоящие слева в формулах (4), будем считать
координатами точки
,
стоящие слева в формулах (4), будем считать
координатами точки
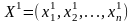 .
Эту точку назовём первым приближением
к точному решению исходной системы,
т.е. к
.
Теперь мы имеем два приближённых решения
системы (3). Этими решениями являются
и
.
.
Эту точку назовём первым приближением
к точному решению исходной системы,
т.е. к
.
Теперь мы имеем два приближённых решения
системы (3). Этими решениями являются
и
.
В четвёртых, сравним эти два приближённых решения на :

Если все неравенства (5) выполняются, то за приближённое решение исходной системы можно выбрать как , так и , поскольку эти два решения отличаются друг от друга не больше чем на .
На этом решение исходной системы методом
простой итерации заканчивается. Если
же хотя бы одно из неравенств (5) не
выполняется, то надо компоненты первого
приближения подставить в правую часть
системы (3) и вычислить второе приближение
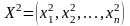 .
Здесь
.
Здесь
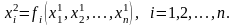
Далее надо сравнить приближения
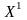 и
и
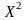 на
по
формуле (5). Строить приближения надо до
тех пор, пока два соседних приближения
на
по
формуле (5). Строить приближения надо до
тех пор, пока два соседних приближения
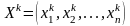 и
и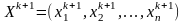 будут отличаться друг от друга не больше
чем на
.
будут отличаться друг от друга не больше
чем на
.
20) Метод Зейделя отличается от метода Якоби лишь тем, что на каждом шаге решения системы уравнений учитываешься предыдущий щаг, т.е. теперь эта система выглядит так:

В методе Якоби решать уравнения системы можно в любом порядке, а в методе Зейделя только сверху вниз.
Итерационный процесс поиска прекращается,
как только выполнится условие![]()
Условием сходимости обоих методов будет являться нер-во
![]()
