1) Вычислительная математика – раздел, в котором рассматриваются методы численного приближения различных математических задач, а также обоснование этих методов.

2) Задачи вычислительной математики – найти верное решение математической задачи, которую невозможно решить аналитическим способом, с наименьшей погрешностью получаемого результата. Вычислительная математика призвана упростить решение сложных матем. задач путем программирования исполнения численных методов при помощи ЭВМ.

3) Слова «устойчивый алгоритм» означают, что чем точнее задаются числа для обработки, тем точнее получается результат, или более строго – устойчивость алгоритма означает, что малым отклонениям в исходных данных соответствуют малые отклонения в результате (решении).

Отсутствие устойчивости (или неустойчивость) означает, что даже незначительные погрешности в исходных данных приводят к большим погрешностям в решении, а зачатую к неверному результату. О таких задачах также говорят, что они чувствительны к погрешностям исходных данных.

Под сходимостью численного метода (алгоритма) понимают способность метода приводить к решению исходной (точному решению) за конечное число шагов,

Численный алгоритм (метод) называется корректным в случае существования и единственности численного решения при любых значениях исходных данных, а также в случае устойчивости этого решения относительно погрешностей исходных данных.

5)

7) Под нелинейными уравнениями понимаются алгебраические уравнения вида  где х- действительное число, - нелинейнаяфункция, а под системой нелинейных уравнений - система вида

не являющаяся системой линейных алгебраич. уравнений

При использовании некоторых методов в качестве исходных данных необходимо указать отрезок, содержащий только один корень данного уравнения Поиск такого отрезка называется отделением корней уравнения. Отделение корней можно проводить двумя способами: графическим и аналитическим.

Графический метод. Действительным корням уравнения соответствуют точки пересечения графика функции с осью Ох. Для нахождения отрезка, содержащего только один корень уравнения, достаточно построить график функции и визуально определить на каких отрезках находятся корни. Точность отделения отрезков зависит от точности построения графиков.

Аналитический метод отделения корней Этот метод отделения корней основан на теореме интервалов. Теорема. Если непрерывная функция f(x) на концах отрезка a b, принимает значения разных знаков, то внутри интервала a b, существует хотя бы один действительный корень уравнения f(x) = 0, т.е. существует такое число x * a b, , что f(x * ) = 0. При этом если на заданном отрезке a b, существует первая производная f (x), сохраняющая знак внутри a b, (f(x) > 0 или f(x) < 0), то корень x * будет единственным. Процесс отделения корней начинается с установления знаков функции в граничных точках а и b. Затем определяются знаки в ряде промежуточных точек, после чего выделяются отрезки, на границе которых функция меняет знак на противоположный. Выделенные отрезки и содержат корень данного уравнения

8) Метод деления пополам

Пусть на отрезке 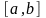локализован корень уравнения .

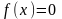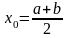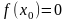Вычисляется точка , если , то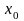 - корень уравнения. Если нет, то из двух половин 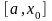, 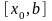выбирают ту, на концах которой функция имеет противоположные знаки и полагают

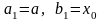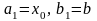если или если .

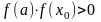Пусть на к-м шаге найден отрезок 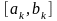. Тогда на к+1 шаге

.

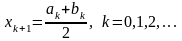
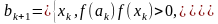Алгоритм завершается, если для некоторого к окажется 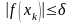, где 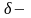требуемая точность решения. Тогда значение корня 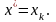Если задана абсолютная точность определения корня 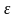, то алгоритм завершается при условии 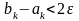. В этом случае за приближенное значение корня 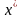принимается

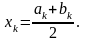
9) Метод хорд

Пусть   — абсциссы концов хорды, Найдем коэффициенты   и   из системы уравнений:

.

Вычтем из первого уравнения второе:

, затем найдем коэффициенты   и  :

, тогда

.

Уравнение принимает вид:

Таким образом, теперь можем найти первое приближение к корню, полученное методом секущих:

Теперь возьмем координаты   и   и повторим все проделанные операции, найдя новое приближение к корню. Таким образом, итерационная формула метода секущих имеет вид:

.

Повторять операцию следует до тех пор, пока   не станет меньше или равно заданному значению погрешности.

10) Метод касательных

Пусть на отрезке   существует единственный корень уравнения (1):  ,

а   существует, непрерывна и отлична от нуля на  . Перепишем (2) следующим образом:

и применим к этому выражению формулу Лагранжа:

Выразим отсюда  :

Метод касательных имеет (когда сходится) квадратичную скорость сходимости

Модифицированный метод касательных

Если мы хотим избежать вычисления производной на каждом шаге, то можно взять   вместо   где   - начальное приближение:

В отличие от обычного метода касательных, в модифицированном методе предоставляется меньше требований к выбору начального приближения, а так же гарантировано отсутствие деления на ноль, если 

11) Метод простых итерации.

Для построения рабочей формулы уравнение преобразуется к виду:

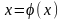. (1)

Далее итерационный процесс строится по формуле

(2)

Для сходимости итерационного процесса (2) необходимо задать произвольное начальное приближение из отрезка 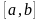, для которого выполняется условие:

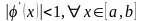(3)

Процесс (3) заканчивается при одновременном выполнении двух услови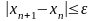й: и . В этом случае значение 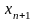является приближенным значением корня нелинейного уравнения на отрезке .

К виду x=(x), удобному для итераций, уравнение f(x)=0 можно привести разными способами. Один из способов заключается в следующем. Уравнение записывается в виде

x=x+сf(x)

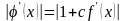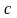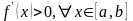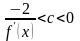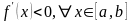Здесь функция . Тогда Константа выбирается из условия сходимости (3). Если производная , то значение выбирается из интервала , если производная , то – из интервала .