31 ) Угол между прямой и плоскостью. Условие принадлежности прямой плоскости. Формула вычисления угла между прямой и плоскостью

Если в пространстве заданы направляющий вектор прямой L

s = {l; m; n}

и уравнение плоскости

Ax + By + Cz + D = 0,

то угол между этой прямой и плоскостью можно найти используя формулу

sin φ =	| A · l + B · m + C · n |
	√A2 + B2 + C2 · √l2 + m2 + n2

32 ) Условие принадлежности двух прямых плоскости

Как известно (§ 46), прямые l₁ и l₂  называются скрещивающимися, если они не лежат в одной плоскости. Пусть а и b — направляющие векторы этих прямых, а точки M₁ и M₂принадлежат соответственно прямым и l₁ и l₂  (рис. 208).

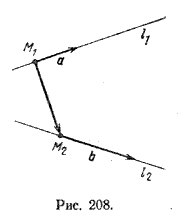
Тогда векторы а, b,   M₁M₂^> не компланарны, и поэтому их смешанное произведение не равно нулю, т. е. (а, b,   M₁M₂^> ) =/= 0.

Верно и обратное утверждение:

если  (а, b,   M₁M₂^> ) =/= 0, то векторы а, b,   M₁M₂^> не компланарны, и, следовательно, прямые l₁ и l₂ не лежат в одной плоскости, т. е. скрещиваются.

Таким образом, две прямые скрещиваются тогда и только тогда, когда выполнено условие

(а, b,   M₁M₂^> ) =/= 0,        (1)

где а и b — направляющие векторы прямых, а M₁ и M₂ — точки, принадлежащие соответственно данным прямым. Условие

(а, b,   M₁M₂^> ) = 0           (2)

является необходимым и достаточным условием того, что прямые лежат в одной плоскости. Если прямые заданы своими каноническими уравнениями

то а = (а₁; а₂; а₃), b = (b₁; b₂;b₃), М₁ (x₁; у₁; z₁), М₂(х₂; у₂; z₂) и условие (2) записывается следующим образом:

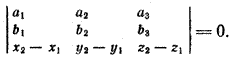
33) Полярная система координат.

Для самого полюса  , а угол   не определён. Не напоминает ли это вам кое-что из темы Комплексные числа? ;-)

Число   называют полярным радиусом точки   или первой полярной координатой. Расстояние не может быть отрицательным, поэтому полярный радиус любой точки  . Первую полярную координату также обозначают греческой буквой   («ро»), но я привык к латинскому варианту, и в дальнейшем буду использовать его.

Число   называют полярным углом данной точки или второй полярной координатой. Полярный угол стандартно изменяется в пределах   (так называемые главные значения угла). Однако вполне допустимо использовать диапазон  , а в некоторых случаях и вовсе возникает прямая необходимость рассмотреть все значения угла от нуля до «плюс бесконечности». Рекомендую, кстати, привыкнуть к радианной мере угла, поскольку оперировать градусами в высшей математике считается не комильфо.

35) Эллипс. Гипербола. Парабола. Эллипс

Пусть на плоскости даны две точки   и   .

Определение. Эллипсом называют множество   точек плоскости таких, что сумма растояний от каждой из таких точек до   и   постоянна. Иными словами,    в том и только том случае, когда  равно фиксированному числу. Точки   ,   называются фокусами эллипса.

Наша цель здесь - получить уравнение эллипса.

Для этого введем систему координат на плоскости так, чтобы точки   и   имели бы координаты   и   соответственно:

Пусть точка   плоскости такова, что   . Здесь   и   - фиксированные положительные числа. Таким образом,   и, как следует из неравенства треугольника,   . Причем равенство здесь выполняется только в том случае, когда   лежит между   и   , и этот случай мы рассматривать не будем.

Перепишем равенство   в координатах:

 (1)

Это уравнение и есть уравнение эллипса в выбранной системе координат. Единственное, что осталось нам сделать - это избавиться в нем от иррациональности и привести его к удобному для восприятия виду, называемому каноническим уравнением эллипса. Для этого перенесем один из радикалов в правую часть и возведем результат в квадрат:

или, после очередных преобразований,

Так как   , то   положительно. Обозначив его через   , перепишем последнее уравнение так:

Разделив обе части этого равенства на   , получим такой результат:

 (1*)

Мы только что установили, что если точка   принадлежит эллипсу, то ее координаты удовлетворяют уравнению (1*). Нам осталось проверить и обратное: если координаты точки   удовлетворяют (1*), то  принадлежит эллипсу, то есть сумма   постоянна.

Найдем расстояния   и   :

 и, учтя, что   , получим

 .

Аналогично,

 .

Из этого и следует равенство   . А это значит, что если координаты точки   удовлетворяют уравнению (1*), то   - точка эллипса. Уравнение (1*) называют каноническим уравнением эллипса.

Обратите внимание, что если в (1*)   , то мы получим уравнение окружности радиуса   , а фокусы при этом совпадут.

36) Эллипсоид. Гиперболоиды. Параболоиды. Цилиндр и конус второго порядка

38 ) Линейная зависимость и независимость векторОВ.

39) Базис. Координаты вектора. Размерность пространства.

40)Ортонормированный базис.

41)Скалярное произведение.

42 )Матрицы в пространстве Rⁿ

43 )Собственные значения и собственные векторы матрицы.

ЗАДАЧИ К ЭКЗАМЕНУ.

1 ) Решение систем линейных уравнений методом Гаусса.

2 ) Решение систем линейных уравнений с помощью формул Крамера и обратной матрицы.

3 ) Разложение вектора по базису в R² и R³.

4 ) Скалярное, векторное и смешанное произведения векторов.

5 ) Задачи на прямую на плоскости , на плоскость , прямую в пространстве.

6 ) Два теоретических вопроса.