7 ) Метод Гаусса.

Покажем, как методом Гаусса можно решить следующую систему:

Обнулим коэффициенты при   во второй и третьей строчках. Для этого прибавим к ним первую строчку, умноженную на   и  , соответственно:

Теперь обнулим коэффициент при   в третьей строке, вычтя из неё вторую строку, умноженную на  :

В результате мы привели исходную систему к треугольному виду, тем самым закончим первый этап алгоритма.

На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:

 из третьего;

 из второго, подставив полученное 

 из первого, подставив полученные   и  .

8 ) Векторы и линейные операции над ними.

Сложение векторов. Пусть   и   – два произвольных вектора. Возьмем произвольную точку О и построим вектор  ; затем от точки А отложим вектор  . Вектор  , соединяющий начало первого слагаемого вектора с концом второго, называется суммой этих векторов и обозначается   (рис. 1).

 

 

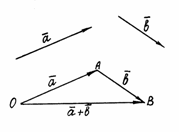
Рис. 1

Ту же сумму можно получить иным способом. Отложим от точки О векторы   и  . Построим на этих векторах как на сторонах параллелограмм ОАСВ. Вектор   – диагональ параллелограмма – является суммой векторов   и   (рис. 2).

 

Рис. 2

Понятие суммы можно обобщить на случай любого конечного числа слагаемых (рис. 3).

Рис. 3

Вычитание векторов. Разностью   векторов   и   называется такой вектор  , который в сумме с вектором   дает вектор  :     .

Если векторы   и   привести к общему началу, то разность представляет собой отрезок, соединяющий их концы и направленный от «вычитаемого» к «уменьшаемому» (рис. 4).

 

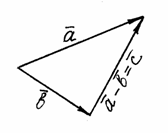
Рис. 4

Таким образом, если на векторах   и  , отложенных из общей точки О, построить параллелограмм ОАСВ, то вектор  , совпадающий с одной диагональю, равен сумме  , а вектор  , совпадающий с другой диагональю, – разности   (рис. 5).

 

Рис. 5

Умножение вектора на число. Произведением вектора   на действительное число   называется вектор   (обозначают  ), определяемый следующими условиями:

1)      ,

2)       при   и   при  .

Очевидно, что при    .

Построим, например, векторы   и   для заданного вектора   (рис. 6).

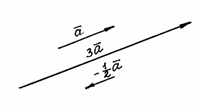
Рис. 6

Из определения следует: два вектора   и   коллинеарны тогда и только тогда, когда имеет место равенство  :

                                                 (2.1)

Свойства линейных операций:

1)      ;

2)      ;

3)      ;  ;

4)      ;

5)      ;

6)      ;

7)      ;  ;

Пусть дан вектор  . Ортом вектора   (обозначается  ) называется вектор единичной длины, сонаправленный с вектором  .

Очевидно,  для любого вектора  .

10 ) Проекция вектора на ось.

Проекция вектора на ось есть скалярная величина, равная произведению модуля проектируемого вектора на косинус угла между положительными направлениями оси и вектора (см. рисунок).

Проекция вектора   на ось   обозначается через a_l или  , а угол между осью   и вектором   будем обозначать так:  . Таким образом,

     (2)

Если   - углы, образованные вектором   с координатными осями Ox, Oy и Oz прямоугольной системы координат, то проекции вектора   на координатные оси будут равны

     (3)

В дальнейшем предполагается, что система координат - прямоугольная.

Модуль вектора через его проекции на оси прямоугольной системы координат вычисляется по формуле

     (4)

т. е. модуль вектора равен арифметическому значению квадратного корня из суммы квадратов его проекций.

Вектор равен нулю, если все три его проекции равны нулю (этим положением пользуются, например, в механике при выводе необходимых и достаточных условий равновесия тела под действием системы сил, проходящих через одну точку).

11 ) Ортонормированный базис. Декартовы координаты вектора.  Если векторы e_1, e₂, e₃ попарно перпендикулярны и длина каждого из них равна единице, то базис называется ортонормированным, а координаты x₁, x₂, x₃ -прямоугольными.

Определение. Три вектора   и   называются компланарными, если они параллельны некоторой плоскости в широком смысле (т. е. или лежат в одной плоскости, или в параллельных плоскостях). После приведения к одному началу компланарные векторы лежат в одной плоскости. Определение. Базисом в пространстве называются три некомпланарных вектора, взятых в определенном порядке; базисом на плоскости называют два неколлинеарных вектора, взятых в определенном порядке; базисом на прямой называют любой ненулевой вектор на этой прямой. Теорема. Каждый вектор в пространстве, плоскости или на прямой может быть разложен по базису пространства, плоскости или прямой соответственно, причем это разложение единственно. Таким образом, если   и  - базис пространства,  - вектор пространства, то   где  - координаты вектора   в базисе  Аналогичные разложения имееют место на плоскости и прямой. При сложении векторов складываются соответствующие координаты, при умножении вектора на число все координаты вектора умножаются на это число. Взаимно перпендикулярные и имеющие единичную длину векторы   образуют ортонормированный базис. Определение. Совокупность точки – начала координат и ортонормированного базиса называют декартовой прямоугольной системой координат.      Прямые, проходящие через начало координат в направлении базисных векторов, называют осями координат, а плоскости, проходящие через оси координат – координатными плоскостями.                                 Рис. 6   Для каждой точки   пространства существует ее радиус – вектор   Под декартовыми координатами точки   понимаются координаты ее радиус – вектора в базисе   т. е.   и  И вообще   или    Если точка   – начало, а точка   – конец вектора   то  Пример. Найти координаты вектора   если   и  . Решение.    Коллинеарные векторы   и   отличаются длиной и направлением (сонаправлены или направлены противоположно), поэтому координаты таких векторов пропорциональны, т.е. векторы   и   коллинеарны тогда и только тогда, когда    Например, векторы   и   коллинеарны.