Д Е Й С Т В И Я С К О Р Н Я М И

АРИФМЕТИЧЕСКИМ КОРНЕМ - ой степени из неотрицательного числа называется неотрицательное число b, для которого

при Например:

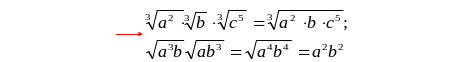
Разложение многочленов на множители

Преобразование многочлена в виде произведения двух или нескольких многочленов (среди которых могут быть и одночлены).

1. Вынесение общего множителя за скобки выполняется по распределительному закону:

2. Группировка. Для этого надо объединить в группы те члены, которые имеют общие множители, и вынести общий множитель за скобки в каждой группе:

Применение формул сокращенного умножения позволяет разложить многочлен на множители:

	Разность квадратов
	Квадрат суммы
	Квадрат разности
	Разность кубов
	сумма кубов
	Куб суммы
	Куб разности

К В А Д Р А Т Н Ы Е У Р А В Н Е Н И Я

Уравнение вида где - некоторые числа ( ), - переменная, называется квадратным уравнением.

Формула корней квадратного уравнения:

Для решения уравнения следует вычислить дискриминант

Значение	Количество решений уравнения
	Одно решение
	Два решения
	Нет решений

Р

Квадратный трехчлен можно разложить на множители следующим образом: решим квадратное уравнение и найдем корни этого уравнения и . Тогда

азложение квадратного трехчлена на множители

Пример

Разложить на множители выражение

Решаем уравнение

Находим корни уравнения

Ответ:

Приведенное квадратное уравнение

Уравнение вида где , называется п р и в е д е н н ы м к в а д р а т н ы м у р а в н е н и е м.

Формула корней приведенного

квадратного уравнения:

Решение приведенного квадратного уравнения можно быстро найти, используя теорему Виета.

Теорема Виета

Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Пример. Решить уравнение

подбираем значения:

Квадратный трехчлен можно разложить на множители

Если уравнение примет вид:

Решение:

Если уравнение принимает вид

Решение:

Д Е Й С Т В И Я С Н Е Р А В Е Н С Т В А М И

1. Неравенства одинакового смысла можно почленно складывать.	a>b + c>d -------- a+c>b+d
2. Неравенства противоположного смысла можно почленно вычитать, оставляя знак того неравенства, из которого производится вычитание.	a<b + c>d ------------ a-c>b-d
3. Неравенства одинакового смысла с положительными членами можно почленно умножать.	Если a>b>0, c>d>0, то ac>bd.
4. Обе части неравенства с положительными членами можно возводить в одну и ту же натуральную степень или извлекать корень одной и той же степени.	Если a>b, то ak >bk и где a>0, b>0; k,n N