§4. Положительные вещественные функции и их свойства.

В предыдущих параграфах было показано, что входные функции линейной пассивной цепи Z(p) = A(p)/B(p) являются положительными вещественными функциями f(p) комплексной переменой p=σ+jω. Изучение положительных вещественных функций ПВФ позволит в дополнение к уже известным свойствам входных функций установить некоторые другие их свойства. Кроме того, установленные ранее свойства входных функций, рассматриваемые как свойства ПВФ, следуют непосредственно из определения ПВФ. Этот факт является подтверждением глубокой и тесной связи между понятиями входных функций линейной пассивной цепи с одной стороны и ПВФ – с другой.

Перейдем к рассмотрению основных свойств ПВФ и для удобства выделим их в виде отдельных пунктов.

1. Величина, обратная положительной функции является положительной вещественной функцией.

Пусть f(p) – ПВФ. Тогда

(25)

что и доказывает высказанное утверждение.

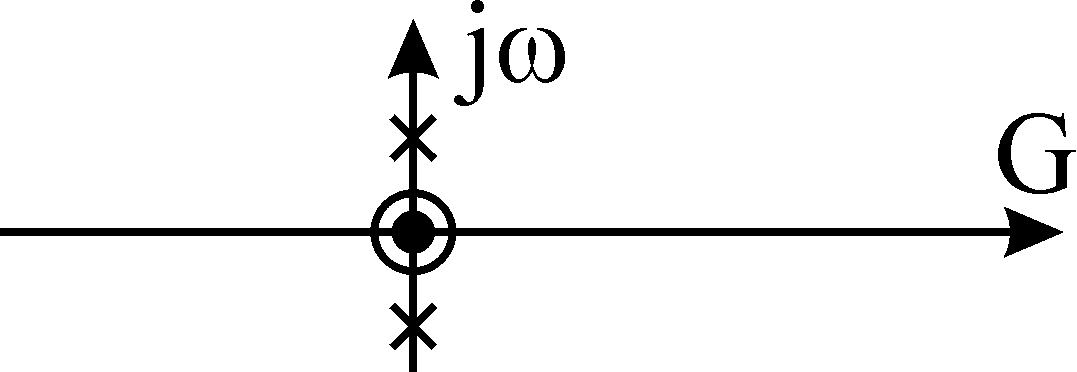
2. Все нули и полюсы f(p) лежат в левой полуплоскости или на мнимой оси. Нули и полюсы на мнимой оси могут быть только простыми (не кратными) с действительными положительными вычетами.

Рассмотрим функцию

Нули функции p₁ = 0, p₃ = -0.5 удовлетворяют условию. На мнимой оси имеются два простых полюса p₂ = j, p₄ = -j. Как известно, вычеты могут быть рассчитаны по формуле

т.е.

где B’(p) – производная от B(p) по p.

Вычет в полюсе на мнимой оси оказывается комплексной величиной, следовательно, функция f(p) не является ПВФ.

Для полиномов A(p) и B(p) со старшими степенями выше двух, когда определение корней громоздко, используют специальные критерии (Михайлова, Найквиста, Гурвица и т.д.), позволяющие без нахождения корней определить их характер, т.е. расположение корней на комплексной плоскости.

3. Все коэффициенты полиномов числителя и знаменателя вещественной положительной дроби – рациональной функции должны быть вещественными положительными числами.

Например, функции

не ПВФ, т.к. старшие степени числителя и знаменателя отличаются друг от друга более, чем на единицу.

Функция

5. Вещественная часть функции f(p) при чисто мнимых значениях p неотрицательна, т.е. Re [f(jω)] ≥ 0.

Пусть

Находим действительную часть f(p) при p = jω.

Отсюда

т.е. f(p) – положительная вещественная функция, т.к. функция f(p) удовлетворяет всем пяти условиям.

Для упрощения вычислений синтезируемая функция записывается в нормированных единицах, т.е. значения коэффициентов этой функции записываются в относительных единица. Нормированные значения определяются из выражений

где R, L, C – абсолютные значения параметров цепи, исоответственно нормирующая частота и нормирующее сопротивление.

§5. Метод синтеза на основе разложения входной функции на элементарные (простейшие) дроби (метод Фостера).

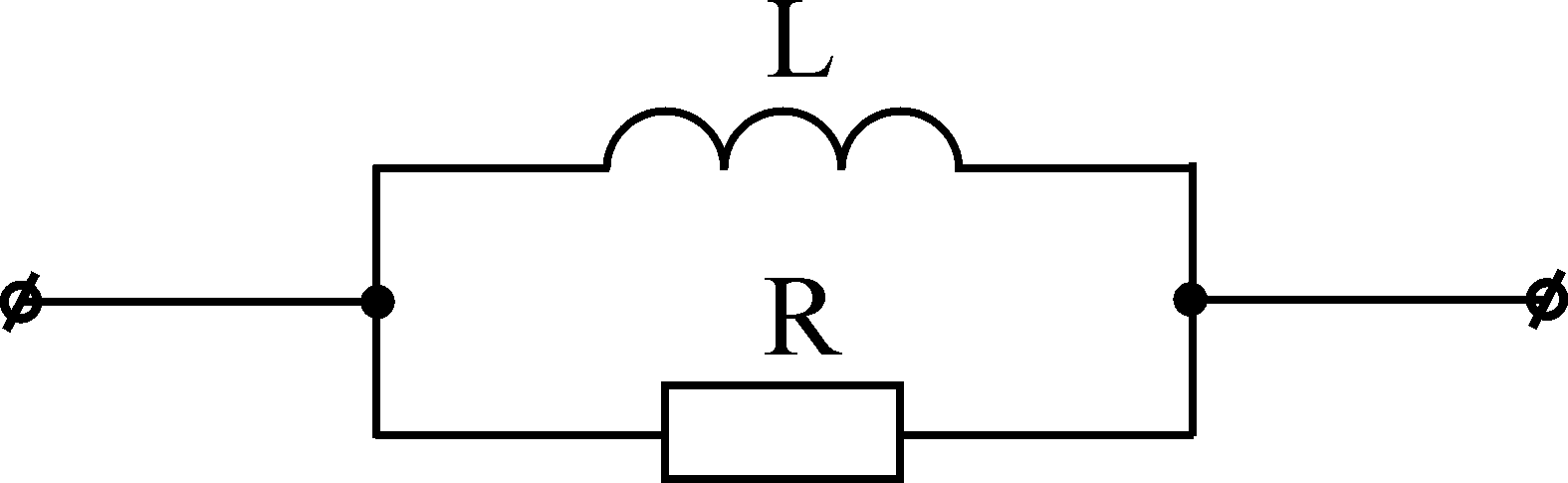
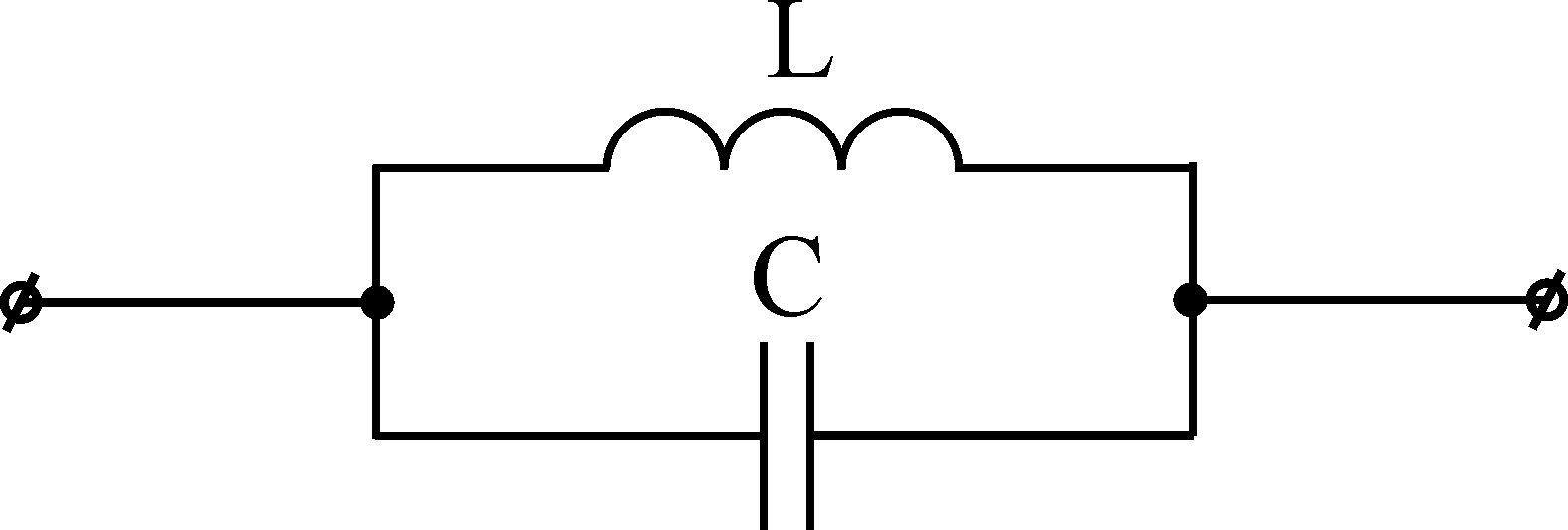
Рассмотрим способ построения цепи, основанные на разложении заданной входной функции на простейшие дроби, которые можно реализовать с помощью элементарных двухполюсников, схемы и соответствующие им выражения входного сопротивления приведены в таблице 2 [6]. В таблице условно показано расположение полюсов (крестики) у нулей (кружочки) входного сопротивления Z(p).

Таблица. 2

Схема		Нули и плюсы

Входную функцию f(p) = A(p)/B(p) можно записать в виде разложения на простейшие дроби

(26)

Первое слагаемое правой части этого равенства представляет собой целую часть дроби A(p)/B(p) и в том случае, если n = m-1, оно отсутствует, т.е. d_∞ = 0. Коэффициенты d_∞, d₀, и d_к являются вычетами функции f(p) в соответствующих полюсах.