ТЕМА
СИНТЕЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
§1. Задача синтеза электрических цепей, её неоднозначность и проблемы выбора решения.
В предыдущих главах проводился анализ свойств цепи, т.е. по известным элементам цепи и схеме их соединения определялись частные характеристики. В инженерной практике часто возникает необходимость построения электрических цепей с заданными заранее свойствами. Такие задачи относятся к области синтеза электрических цепей, которые могут вообще не иметь решения или иметь несколько решений. Так, например, попытка построения пассивной линейной цепи с отрицательным значением вещественной части входной функции обречена на неудачу, т.е. функция, удовлетворяющая условию Re Z(jω)<0, оказывается физически нереализуемой. Отмеченное ограничение не является единственным и чтобы решить задачу синтеза, необходимо отчетливо представлять свойства входных функций. В задачу синтеза электрической цепи входят:
1) аппроксимация заданных частотных характеристик в виде функций, удобных для реализации;
2) реализация электрической цепи.
Задачи аппроксимации связаны с выбором подходящих функций и определением коэффициентов аппроксимации по заданным условиям точности. Эта задача здесь не рассматривается.
Задачу реализации цепи мы будем называть задачей синтеза. Решение задачи синтеза не может быть однозначным, т.к. существует множество цепей с одинаковыми характеристиками. Из них надо выбрать наилучшее решение. Критерием выбора решения может быть наименьшее число элементов в схеме, минимальная стоимость реальной схемы и т.д. Эти критерии зависят в значительной степени от значения технологии выполнения схем, от опыта инженера, осуществляющего синтез цепи.
Здесь рассматриваются только самые простые приемы синтеза линейных цепей по заданным частотным характеристикам в виде дробно-рациональной функции комплексного входного сопротивления Z(p) (входной проводимости Y(p)), где p = δ + jω – комплексная частота.
Основные идеи синтеза линейных пассивных цепей, составленных из элементов R, L, C, заключаются в реализации такого преобразования частотных характеристик, при котором каждый член математического выражения характеристики соответствовал бы определенному элементу цепи, а взаимосвязь между этими членами соответствовала бы определенной схеме соединений.
§2. Фундаментальные свойства схемных функций цепей.
Схемные функции цепи (входное сопротивление, входная проводимость, передаточные функции) обладают многими общими свойствами. Z(p), Y(p) и K(p) являются функциями комплексной частоты p=δ+jω.
Прежде всего отметим, что вещественная часть входного сопротивления Z(p) при p = jω (или входной проводимости Y(jω)) должна быть неотрицательной величиной. Это следует из того, что пассивная цепь может только поглощать энергию, т.е. средняя мощность, подводимая к пассивной цепи, должна быть неотрицательной.
(1)
где P
– активная мощность;
– комплексное действующее значение
напряжения;
- комплексно-сопряженное действующее
значение тока.
Это неравенство можно переписать так:
(2)
откуда следует
или
. (3)
Часто оказывается удобным записывать входные функции в виде Z = zejφ, причем величина φ = arg Z должна удовлетворять условиям
(4)
Из условия (3)
следует, что cos
φ
не может быть отрицательной величиной,
т.е. значение φ не должно по модулю
превышать
.
(5)
Выясним зависимость входных функций от частоты внешнего воздействия.
В качестве примера рассмотрим входное сопротивление двухполюсника, схема которого изображена на рис. 1.
(6)
Отсюда, вещественная часть входной функции пассивной электрической цепи является четной функцией частоты
(7)
а мнимая
(8)
– нечетной функцией частоты.
Кроме того, модуль и аргумент входной функции также являются соответственно четной и нечетной функциями частоты.
Нечетность мнимой части входной функции означает, в частности, что при стремлении частоты к нулю реактивная составляющая входной функции может только или обращаться в нуль, или претерпевать разрыв.
Рассмотрим электрическую цепь рис.2.
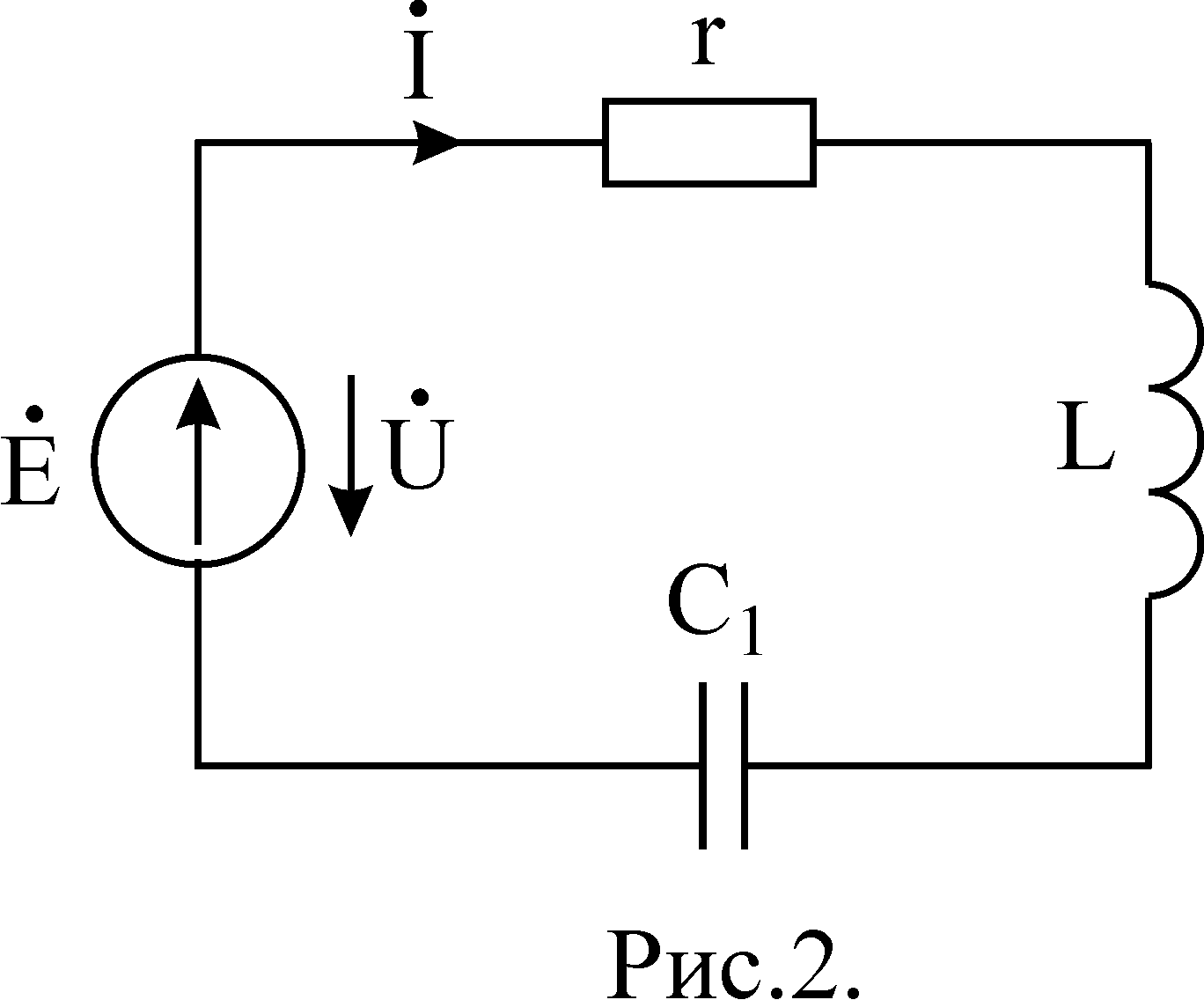
Комплексное действующее значение тока определяется из уравнения
(9)
Умножим обе части уравнения на сопряженный ток.
(10)
В этом равенстве правая часть определяет комплексную мощность, отдаваемую источником ЭДС, изменяющемся по гармоническому закону.
(11)
Запишем это уравнение в матричной форме для сложной цепи [Л.1].
(12)
где
– транспонированная матрица; [r],
[L]
и
– матрицы параметров контуров.
Обозначив
(13)
(14)
(15)
получим
(16)
где F0, T0, V0 называются обобщенными энергетическими функциями.
В правую часть (13) вышли энергетические функции F0, T0, V0, характеризующие расходуемую энергию в сопротивлении r и накапливаемую энергию в магнитном и электрическом полях соответственно индуктивности и емкости пассивной цепи. Значение энергии не может быть отрицательным, поэтому F0 ≥ 0, T0 ≥ 0 и V0 ≥ 0. Энергетические функции вещественны, т.к. они являются функциями квадратов токов и параметров r, L, и C пассивной электрической цепи.
Установим связь энергетических и схемных функций двухполюсника.
Входное сопротивление в операторной форме (заменив jω на p=σ+jω)
(17)
Входная проводимость по аналогии
(18)
В формулах (14) и (15) |I(p)|2, |E(p)|2, F, T, V – положительные вещественные величины, поэтому схемные функции Z(p) и Y(p) удовлетворяют двум условиям:
1) при действительном значении p = σ
т.е. Z(σ) и Y(σ) действительны при действительном p = σ;
2) комплексным значениям p с неотрицательной вещественной частью Rep=σ≥0 соответствуют комплексные значения Z(p) и Y(p), имеющие неотрицательные вещественные части Re Z(p) ≥ 0 и Re Y(p) ≥ 0. Функции, удовлетворяющие этим двум условиям, называют положительными вещественными функциями (ПВФ). Таким образом, входные функции двухполюсника – положительные вещественные функции.
При p = jω входное сопротивление двухполюсника
(19)
Для любого реактивного двухполюсника
где
и (20)
Из (17) следуют дополнительные свойства реактивных двухполюсников:
крутизна частотных характеристик
и
всегда положительна; (21)
частотная характеристика определяется чередованием простых нулей и полюсов; с увеличением угловой частоты за нулём следует полюс, за полюсом – нуль.
Эти два условия называются теорией Фостера.