Спектральный метод.

1. Временное и спектральное представление сигналов.

Сигналы можно представлять двояко: в виде функций времени и в виде частных спектров. Например: гармоника, выражаемая функцией Acos(t+):

Временное представление гармоники

Спектральное представление гармоники

При комплексной форме записи косинусоиды

вводится чисто математическое понятие отрицательной угловой частоты (и -).

Так как гармоника – простейшая периодическая функция, то ее амплитудный и фазовый спектры изображаются наиболее просто, в виде одиночных ординат А и , соответствующих заданной угловой частоте.

Совокупность гармоник, на которые раскладывается функция f(t), называетсяспектром. Амплитуды гармонических составляющих равныA_n, а начальные фазы_n. Такой спектр называетсядискретным (линейчатым). Постоянную составляющую рассматривают как гармонику с нулевой частотой и амплитудой.

Если периодический сигнал несинусоидален, то он может быть разложен в ряд Фурье, т.е. представлен в виде дискретного ряда гармоник (предполагается, что сигнал удовлетворяет условиям Дирихле).

, (1)

амплитуды A_nи начальные фазы_nвычисляются по формулам:

. (2)

Здесь коэффициенты разложения

(3)

(4)

Основная угловая частота ₁=2/T.

Чтобы наглядно представить спектр, пользуются спектральными диаграммами двух типов: амплитудными и фазовыми. При их построении вдоль оси абсцисс откладывают частоты n₁(n=0, 1, 2…), а вдоль оси ординат – амплитудыA_nи начальные фазы_n. Совокупность построенных ординатA_nи_n образуют дискретный (линейчатый) амплитудный и фазовый спектры данного несинусоидального периодического сигнала.

Комплексная форма записи ряда Фурье

(5)

Комплексные амплитуды вычисляются по формуле

(6)

Частоты n₁(n=0,1,2…) образуют на оси ряд равноотстоящих точек. Совокупность амплитуд соответствующих гармоники совокупность ординат, равных аргументам_n=-_-n, отложенных против соответствующих частот, образуют тоже линейчатый амплитудный и фазовый спектры.

Таким образом, в зависимости от формы записи ряда Фурье (тригонометрической или комплексной), так же как и в случае одиночной гармоники, получаются спектры двух видов: на положительной полуоси или на обеих полуосях частот.

Спектры некоторых типовых несинусоидальных периодических сигналов.

Периодическая последовательность прямоугольных импульсов.

Шкала частот для удобства проградуирована по номерам гармоник n.

Амплитудный спектр

Фазовый спектр

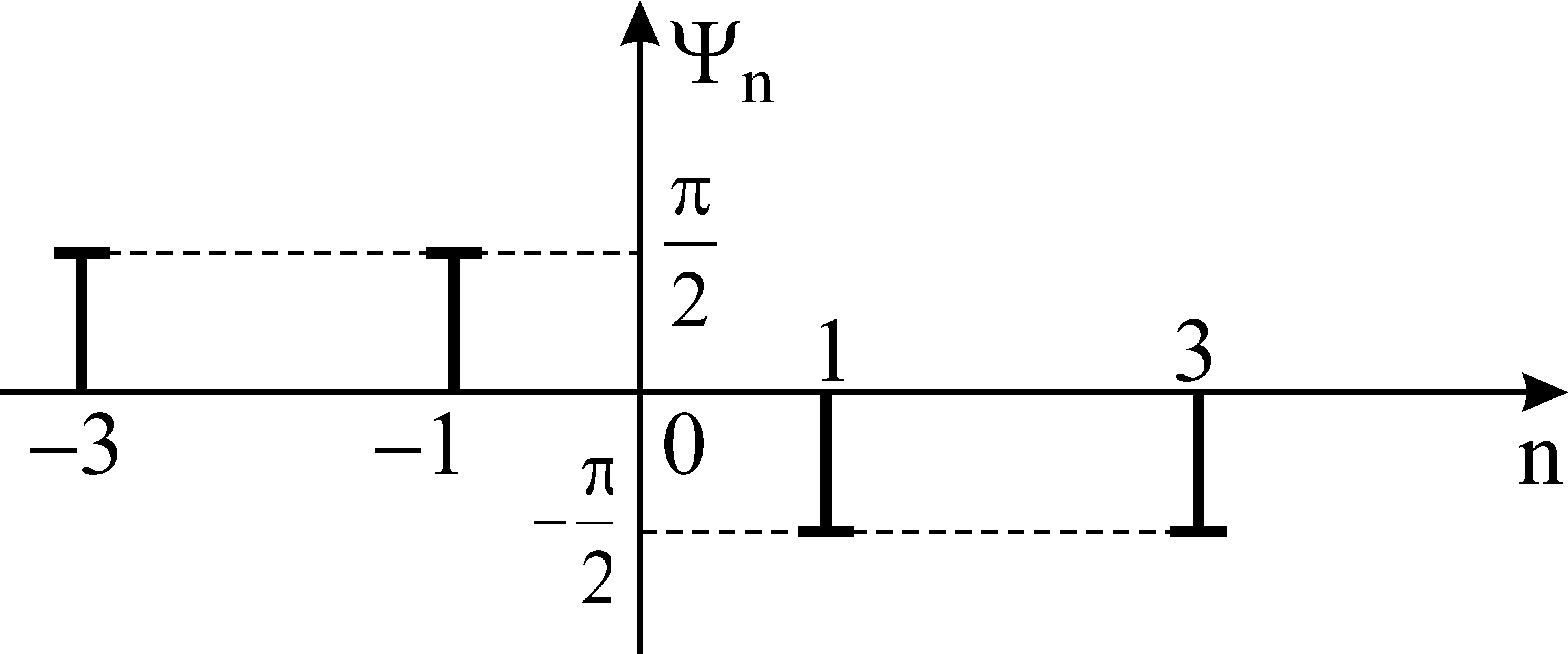
Сигнал может быть смещен по шкале времени в сторону опережения на t₁/2.

В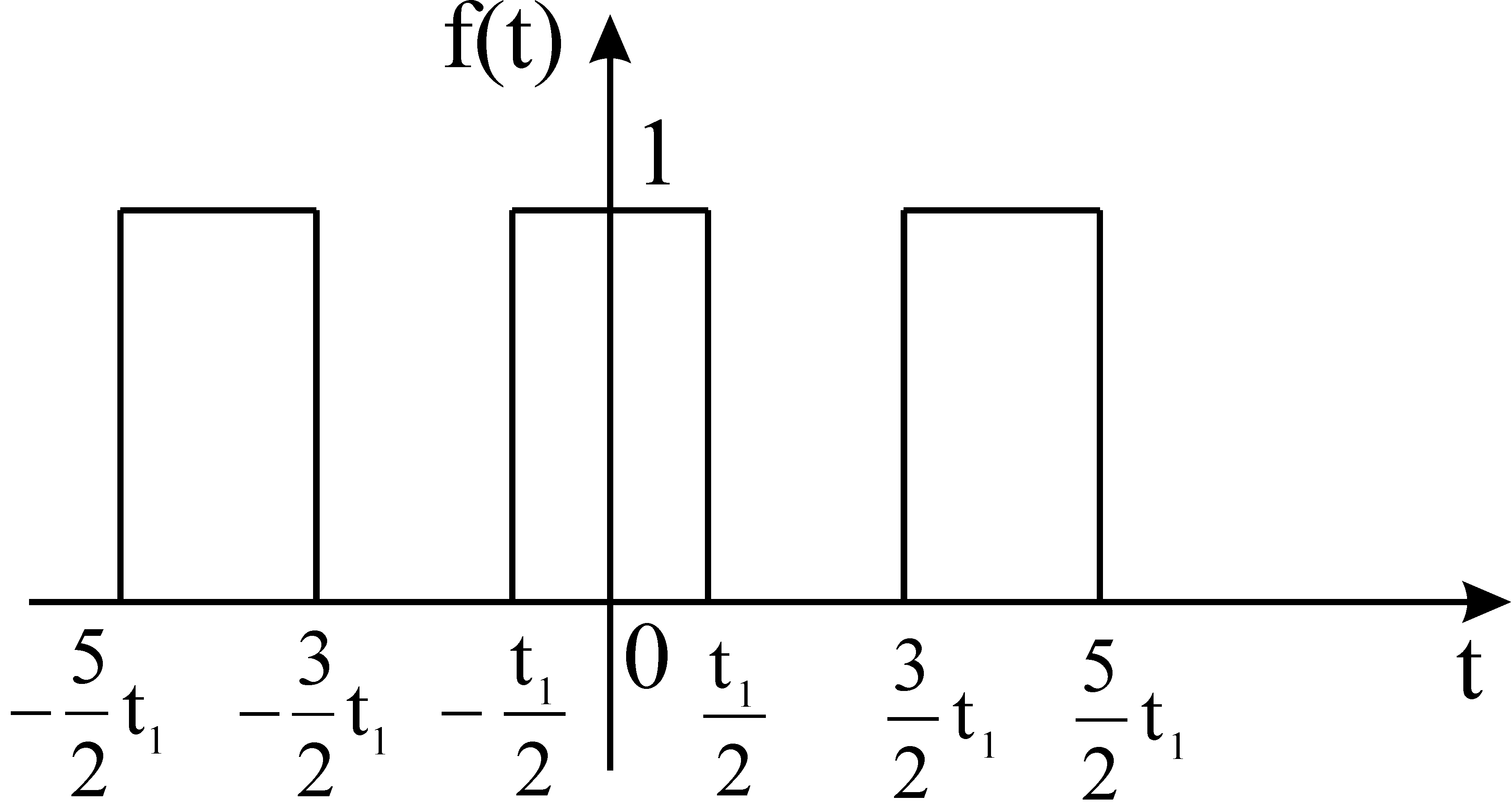виду того, что функцияf(t) симметрична относительно оси ординат, коэффициентыдействительные; когда они положительны, начальные фазы_nравны нулю, а когда отрицательны, то_n=. Так как в данном случае коэффициентыдействительные, можно не рисовать в отдельности амплитудный и фазовый спектры, а ограничится только изображением по шкале частот коэффициентовс учетом их знаков.

Сравнивая рисунки видно, что сигналы имеют одинаковые амплитудные спектры. Следовательно, сдвиг сигнала во времени не влияет на амплитудный спектр, а изменяет только фазовый спектр.

Последовательность прямоугольных импульсов, симметричных относительно оси ординат, с периодом, значительно превышающим длительность импульса

Величина N=T/t₁называется скважность импульсов.

ДляN=Sспектр на основе типовой кривой, которая в масштабеNизображает огибающую коэффициентов.

Число спектральных линий между началом отсчета по шкале частот и первым нулем огибающей, равное числу спектральных линий между соседними нулями, составляет N-1. Чем больше скважность импульсов, тем гуще линейчатый спектр.

Последовательность треугольных импульсов.

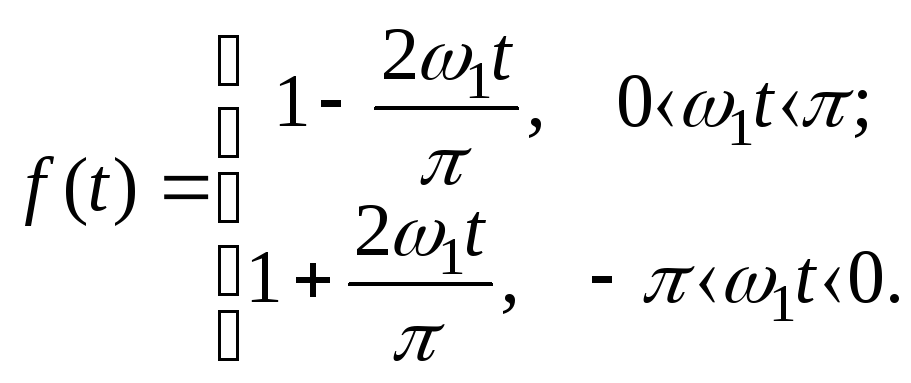
Спектр

для n– четных (cosn=+1)=0;

n– нечетных (cosn=-1)

n=0, A₀=0.

Спектры линейно связаны с сигналами.

Частотный подход к исследованию процессов в электрических цепях удобен тем, что позволяет учитывать частотные свойства цепей при прохождении сигналов, судить о распределении энергии в спектре и оценивать значимость отдельных участков спектра. В сочетании с методом наложения дает возможность исследовать переходные процессы в ЛЭЦ.

Временное и спектральное представления сигналов равноправны и взаимозаменяемы. Предпочтение отдается тому подходу, который в данном конкретном случае оказывается наиболее удобным.