9.5 Смешанный или комбинированный метод расчета переходных процессов.

Решение ищется как в классическом методе в виде .

Одно слагаемое ищется как в классическом методе, т.е. в установившемся режиме.ищется операторным методом . Т.к. свободные составляющие определяются запасами внутренней энергии, значит в операторной схеме внешние источники цепи отсутствуют, то не будет и внешних корней, обусловленных действием этих источников.

Начальные условия для свободных составляющих ищем из уравнений:

Т.о. мы избегаем двух операций:

а)нахождение постоянных интегрирования;

б)выделение принужденной составляющей.

, ,, где

.

Составим операторную схему замещения

.

Окончательно имеем

.

10. Расчет переходных процессов при включении цепи к источнику с произвольным сигналом.

Сигнал– может иметь произвольную форму. Иногда его разбивают на элементарные сигналы, сдвинутыми во времени. От каждого элементарного сигнала рассчитывается реакция цепи и затем суммируется, т.е. МН.

В основе элементарных сигналов используется:

единичный скачок; единичный импульс.

10.1 Единичная функция и запаздывающая единичная функция.

Единичная функция или единичный скачок- это функция, подчиняющееся следующему закону: до момента она равнялась 0, в моментона возрастает до 1 и в дальнейшем не меняется

Умножение единичной функции на любую другую функцию времени оставляет последнюю без изменения при всех значениях и обращает в 0 при .

Единичная запаздывающая функция или запаздывающий скачок- это функция подчиняющаяся следующему закону:

при всех она равна 0

при всех она возрастает до 1 и в дальнейшим не меняется.

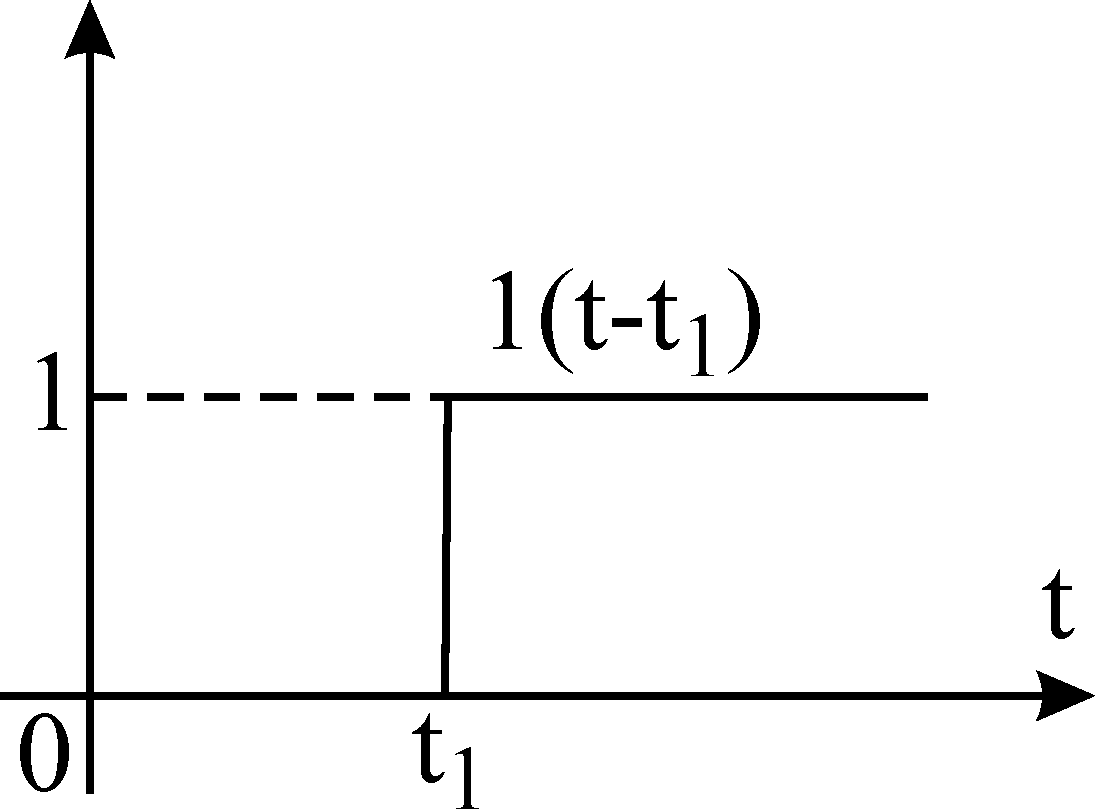
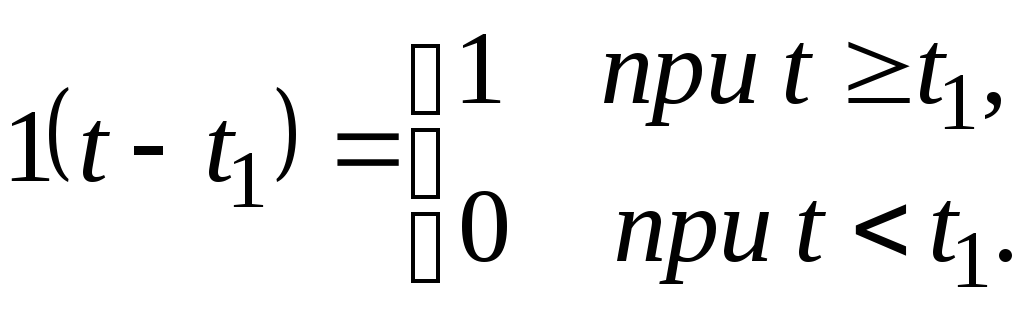
Умножение этой функции на любую другую функцию времени оставляет последнюю без изменения при всех и обращает в 0 при .

Например :

Единичные функции указывают момент возникновения этого или иного сигнала.

10.2 Переходные характеристики или переходные функции цепи.

Переходной характеристикой называется уравнение, составленное для участка цепи или для всей в целом, которое описывает переходный процесс, если цепь подсоединяется к источнику с постоянным входным сигналом равным 1 (1А или 1В).

–переходная характеристика для тока

–переходная характеристика для напряжения

–переходное сопротивление

–переходная проводимость

, т.к , то, (1)

, (2)

;, (3)

.(4)

10.3 Порядок расчета переходных характеристик

1. Каким бы не было заданное входное воздействие или ток источников, его принимают равным 1В или 1А.

2. Определяют ННУ и и т.д. т.е. для полученной цепи рассчитываем п/пр. любым методом. Полученные уравнения для идадут соответствующие переходные характеристики.

Пример.

Найти переходную характеристику по току для цепи

для ветви с сопротивлением при воздействии на входе ИТ

, .

Решение

1. 

2. ННУ

3. 

4. 

5. 

, где ,, .

6. ЗНУ наедем из после коммутационной схемы:

7. Полное решение

8. Переходное характеристика безразмерна:

10.4 Расчет переходных процессов при включении цепи к источнику с сигналом скачкообразной формы.

Прямоугольный импульс как разность двух функций.

зная реакцию цепи на единичную функцию, можно найти реакцию той же цепи на производную функцию.

С помощью формул:

Обобщим:

(1)

Напряжение участка цепи:

(2)