9.1 Изображение некоторых простейших функций по Лапласу.

1. Изображение постоянной

т.е .

2. Изображение показательной функции

Если то .

3. Изображение синусоиды (косинусоиды)

; .

4. Дифференцирование оригинала

, то – учитывает начальное значение в момент.

5. По теореме интегрирования

–учитывает начальное значение интеграла в момент.

9.2 Связь между операторными токами и напряжениями в основных элементах цепи. Операторные схемы замещения.

Операторный ток , напряжение , ЭДС.

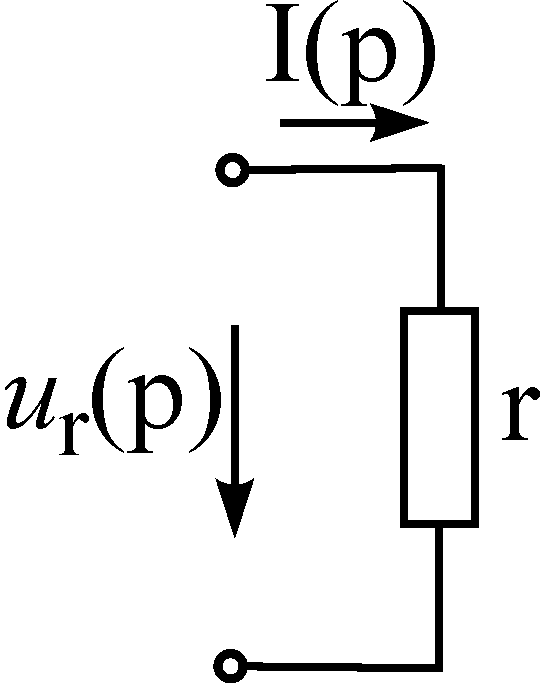
1)

2)

играет роль операторного сопротивления индуктивности ;

–учитывает начальное состояние индуктивности условный источник напряжения.

3)

;

;

–операторное сопротивление емкости; – учитывает начальное состояние емкости условный источник напряжения.

9.3 Законы электрических цепей в операторной форме

1 закон Кирхгофа

2 закон Кирхгофа

В операторной форме

Закон Ома

, – операторное сопротивление, составляется по законам цепи переменного тока, только вместоставится.

–операторная проводимость.

Пример 1

Операторная схема замещения

;

;

.

Пример 2

Нужно рассчитать цепь до коммутации.

Это свободные составляющие токов, индекс св. здесь опущен.

Порядок расчета операторным методом.

1. Рассчитывается схема до коммутации и определяются ННУ, т.е ;.

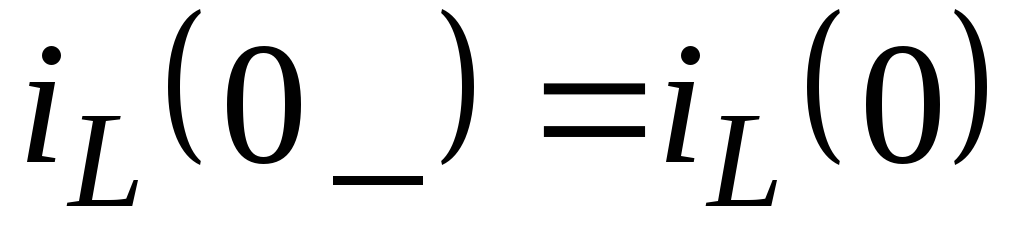2. С учетом найденных ННУ составится операторная схема замещения.

3. От полученных операторных изображений переходит к оригиналам , т.е к функциям времени.

9.4 Нахождение оригинала по известному изображению.

Пусть изображение получили в виде простой дроби

(1)

тогда оригинал находится по теореме разложения.

1) ,– корнидействительные и различные

2)Дробь – несократимая, т.е. многочленыиобщих корней не имеют, и– действительные числа.

3) Если – корни знаменателя, то числитель не должен обращаться в ноль:– корни числителя.

4) Корни знаменателя не должны обращать производную знаменателя в ноль: .

Теорема разложения:

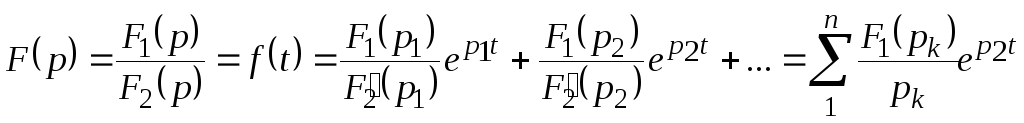
Порядок расчета по теореме разложения .

1. Находим корни знаменателя

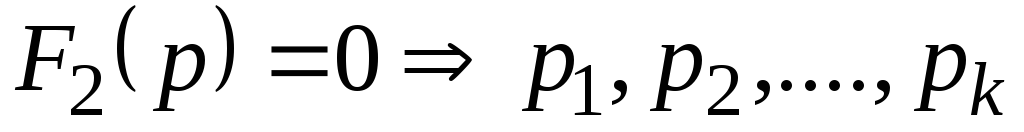
2. Поочередно подставляем эти корни в числитель

3. Находим производную знаменателя и поочередно подставляем в нее найденные корни

4. Вычисляются отдельные слагаемые суммы и складываются.

Замечания к применению теоремы разложения.

1. Слагаемые, полученные при подстановки, всегда рассматриваются отдельно. Именно они выделяют принужденные составляющие.

2. Теорему разложения можно применить при наличии нулевого корня следующим образом :

, – нулевого корня не имеет.

,

.

Тогда

3. Теорему разложения нельзя применить, если корни равные. В этом случае используют искусственный прием. Полагают, что корни разные ит.е.и расчет ведут как для разных корней. Затем, получают неопределенность и раскрывают ее.

4. Если корни комплексные, то они будут сопряженными, поэтому выделяют действительную часть и удваивают, мнимые уничтожаются.

Пример 1

Операторная схема замещения с учетом ННУ:

Находим корни :

; ; .

Тогда

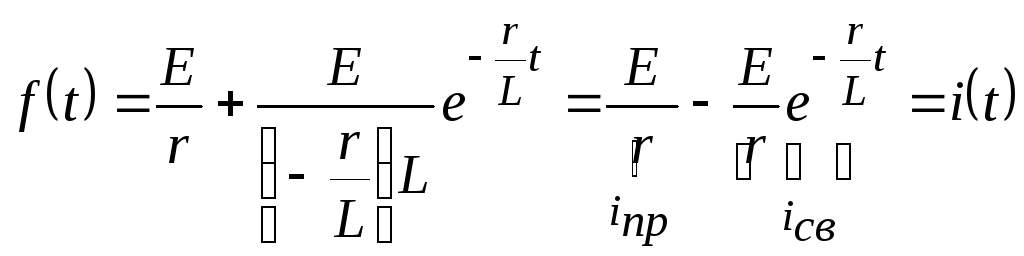
Пример 2

;

или .

а) Получими

б) предельный случай апериодического разряда конденсатора.

,

.

,

в) колебательный процесс.

.

.

Пример 3

,

,

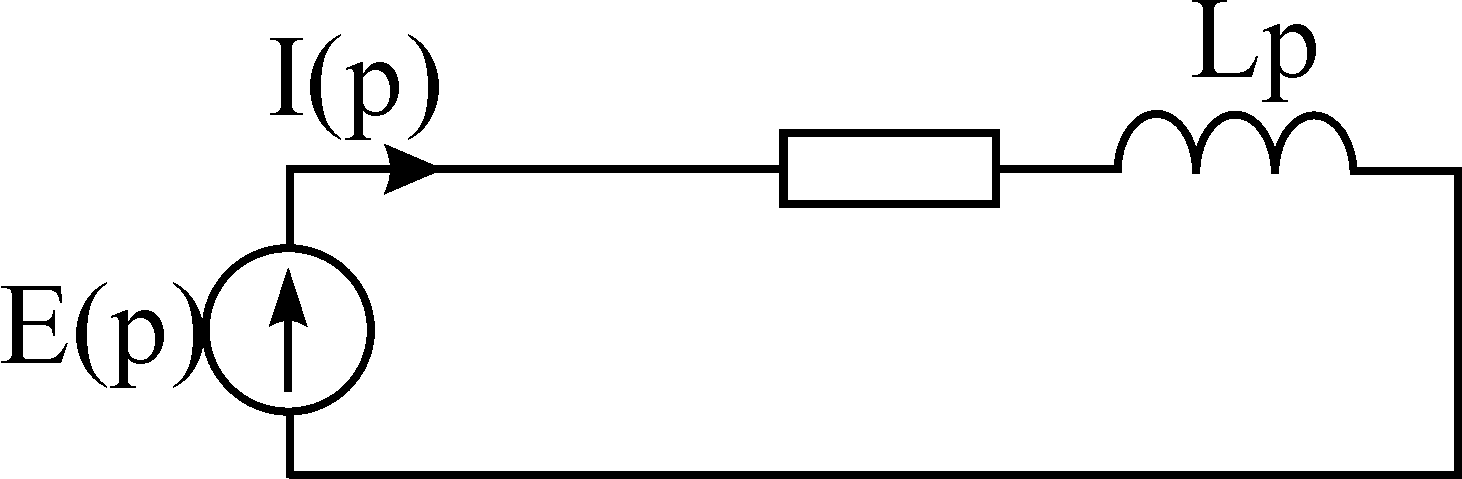
, где ,

.

Итак, изображение тока

. Найдем .

, .

Тогда

Оригиналы тока по теореме разложения:

Учтем следующие преобразования:

; ;;;;

Тогда ток:

Операторный метод для цепей с синусоидальными источниками применить нецелесообразно.