2. Включение цепи источнику синусоидального напряжения.

Пусть цепь подключается к источнику гармонической ЭДС.

.

Определим:

.

Начальные условия:

Характеристическое уравнение :

Корень

.

Принужденный ток будет :

где

,

Свободная составляющая тока :

Тогда переходный ток в цепи будет:

.

Для нахождения постоянной интегрирования получаем :

Окончательно имеет:

Здесь -фаза включения, от нее зависит какой будет переходный процесс.

а) если ;. П/пр не будет. Это называется удачное включение.

б) ;

В момент включения начальный свободный ток максимален, а именно , и ток переходного режима:

достигает экстремального значения (положительного или отрицательного) в конце первого полу – периода.

Однако даже в предельном случае, когда и , следовательно, ток не может превышать амплитуду установившегося режима более чем вдвое.

8.9 Переходный процесс в цепи

Заряд конденсатора ЭДС

а)

Найти

Дифференциальное уравнение цепи :

Его решение :

Принужденное напряжение на емкости равно ЭДС источника:

.

Определим характеристическое уравнение по дифференциальному, заменив ,. Откуда находим корень:

.

Свободная составляющая .

–постоянная времени

Переходное напряжение

Постоянная интегрирования находится по начальному условию при

.

Окончательно имеем:

б) Включение в цепь r, C источника синусоидального напряжения.

Воздействие . Дифференциальное уравнение цепи :

Найти

Тогда

Его решение ищем в виде:

Найдем принужденную составляющую :

,

где

,

,

.

Окончательно имеем

..

Определим характеристическое уравнение :

Из него имеем:

Откуда

Таким образом, общее решение будет :

Для определения постоянной интегрирования положим

Искомое напряжение на емкости:

(1)

а ток в цепи

(2)

Здесь – фаза включения

1) – удачное включение, п/пр не будет.

2)

Как видно из графика ток может значительно превышать амплитуду установившегося режима, а напряжение на емкости возрастает, но не может превысить удвоенной амплитуды.

Выводы по цепям первого порядка.

1. В цепях 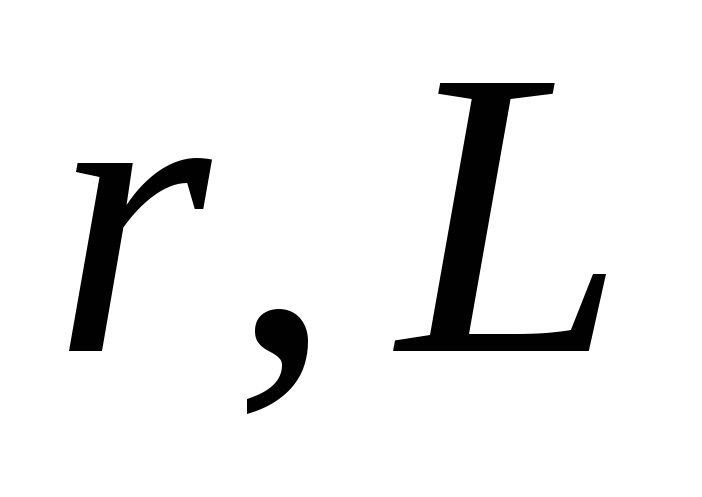корень характеристического уравнения равен

(1), , .

2. В цепях корень равен

(2), , .

где –эквивалентное сопротивление цепи относительно зажимов реактивного элемента в момент коммутации.

3. Из этого вытекает способ нахождения корней характеристического уравнения без его составления и решения.

Из цепи удаляются все источники. Для полученной цепи относительно зажимов реактивного элемента находится входное сопротивление

Затем по (1) или (2) находится корень.

8.10 Анализ переходных процессов в цепях второго порядка.

1. Свободный переходный процесс в контуре r,l,c.

Цепь на размыкание т.е. источник ЭДС отключается и в цепи свободный процесс.

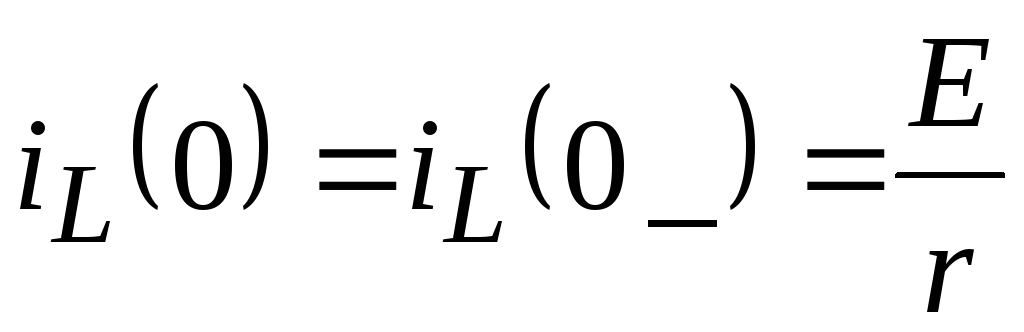
Пусть .

ННУ:

;

.

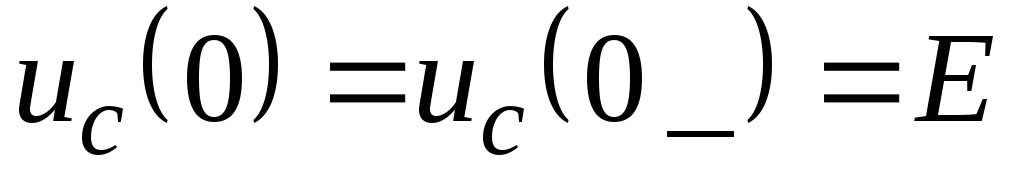Напряжение переходного процесса , ,

Характеристическое уравнение:

или

Его корни :

Введем обозначение :

,

,

тогда

–резонансная частота.

Рассмотрим возможные три случая

1) , или

(апериодический процесс – корни действительные ). Свободная составляющая имеется в виде :

2) , т.е. ,

(процесс критический, корни одинаковые). Свободная составляющая ищется в виде:

3) т.е.

(процесс колебательный). Корни характеристического уравнения комплексные и сопряженные

Введем обозначение – частота свободных колебаний. Тогда корни

Величина связана с добротностью

где 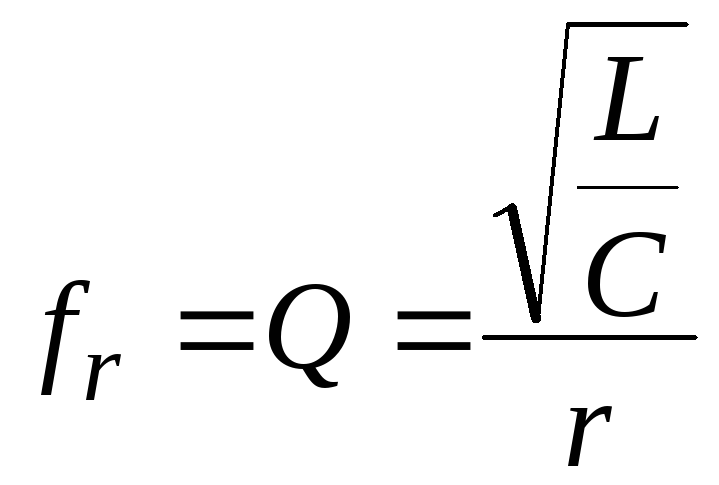. Если, то, т.е. при большой добротности.

Свободная составляющая ищется в виде :

(1)

или

(2)

где

,