8.7. Определение свободных составляющих п/пр.

(1) (2)

(3)

А- постоянная интегрирования, определяемая из начальных условий;

Р- показатель затухания, он един для всех токов.

Продифференцируем по:

(4)

тогда

Проинтегрируем :

(5)

тогда

Систему уравнений для свободных составляющих можно переписать в виде:

Решая систему можно найти токи . Сделать это можно через определитель матрицы

и т.д.

1. Искусственный прием составления

характеристического уравнения .

1. Из схемы удаляются все источники

2. Места источника тока разрываются а источника напряжения закорачиваются.

3. Для полученной пассивной цепи относительно любой ветви находится комплексное входное сопротивление.

Пример

2. Свойства корней характеристического уравнения

Характеристическое уравнение составляется для цепи без источников, поэтому отсюда вытекают свойства:

1. Вещественная часть корней характеристического уравнения всегда <0, т.е.

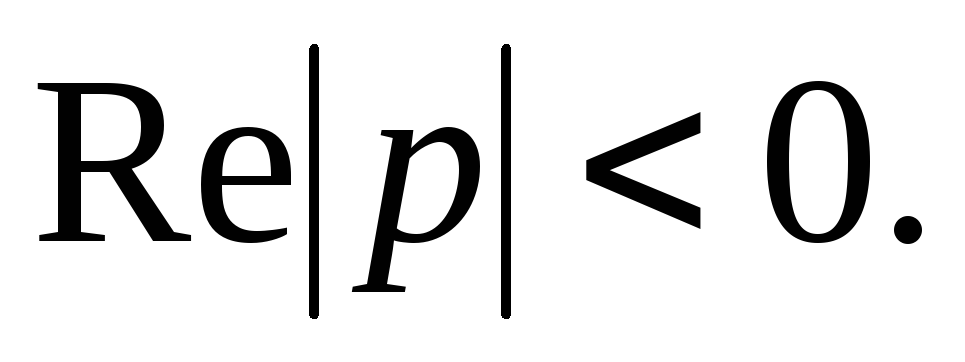
Если корни комплексные, то они будут сопряженными по парам с отрицательной действительной частью.

Если цепь без потерь, то корни будут чисто мнимые

3. Определение характера свободной составляющей по виду корней характеристического уравнения.

   1. Цепь первого порядка (т.е один реактивный элемент), корень будет один, ,

где –показатель затухания.

–время, в течении которого илиуменьшается враз.

Время переходного процесса практически

2. Цепь второго порядка (два реактивных элемента), два корня.

Здесь рассмотрим три случая корней характеристического уравнения.

1. корни действительные, отрицательные, разные

,

Пусть для определенности, тогда кривые для свободных составляющих

б) корни действительные, отрицательные, равные

и

Процесс апериодический (его называют критическим в данном случае)

корни комплексные

–показатель затухания

–частота свободных колебаний

Свободная составляющая тока ищется в виде

(1)

(2)

–начальная фаза свободных колебаний

О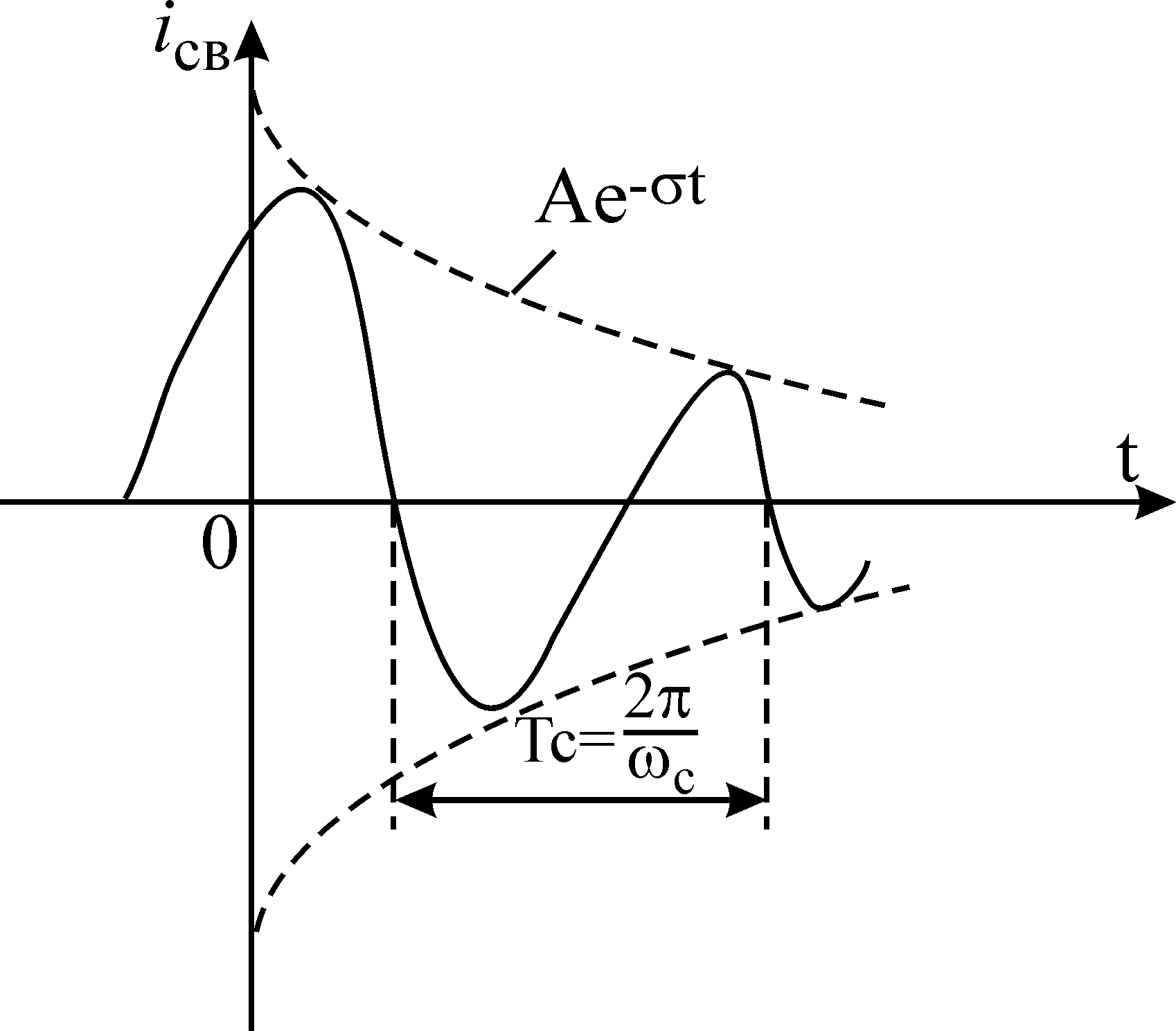тношение двух амплитуд, следующих друг за другом, называютдекрементом затухания .

Логарифмический декремент затухания

3. Определение постоянных интегрирования.

Основано на использовании начальных условий

1. цепь первого порядка

;

Берем момент времени

2) цепь второго порядка

Т.к постоянных интегрирования две , а уравнение одно, то нужно продифференцировать первое уравнение

Берем момент времени и воспользовавшись независимыми и зависимыми НУ:

8.8 Анализ переходных процессов в цепях первого порядка

1. Короткое замыкание в цепи

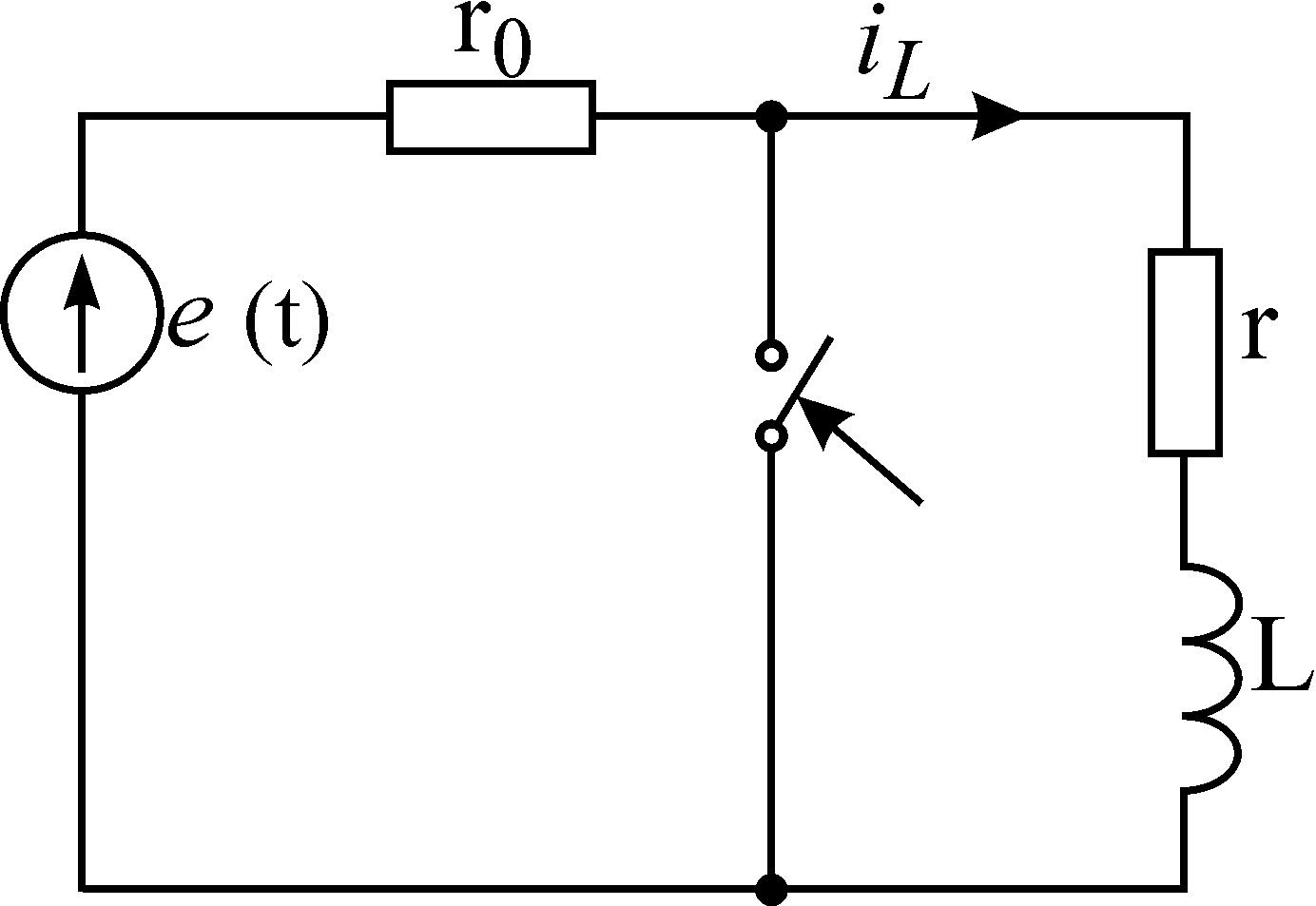
Положим, что цепь , присоединенная к источнику постоянного или переменного напряжения, замыкается принакоротко. В образовавшемся при этом контуреблагодаря наличию магнитного поля индуктивной катушки ток исчезает не мгновенно : ЭДС самоиндукции, обусловленная убыванием магнитного потока, стремится поддержать ток в контуре за счет энергии исчезающего магнитного поля. По мере того как энергия магнитного поля постепенно рассеивается, превращаясь в сопротивлении в тепло, токв контуре приближается к нулю.

Общее решение , т.к. цепь отсоединяется от источника питания.

Характеристическое уравнение цепи :

Тогда

Возьмем момент времени , тогда

a)

б)

Чем меньше, тем быстрее закончится п/пр.