8.5 Определение начальных условий

1. . В начале определяет ННУ. Для этого любым методом рассчитывается цепь до коммутации и определяются токи в индуктивностях и напряжение на емкостях. Положим и получим значения в момент коммутации.

2. . Для момента времени используя найденные независимые НУ. Цепь рассчитываем как цепь постоянного тока.

3. . Для определения производных тока и напряжения в момент коммутации нужно для после коммутационной схемы составить уравнение по законам Кирхгофа. Они справедливы для любого момента времени, значит будут справедливы и для . Положив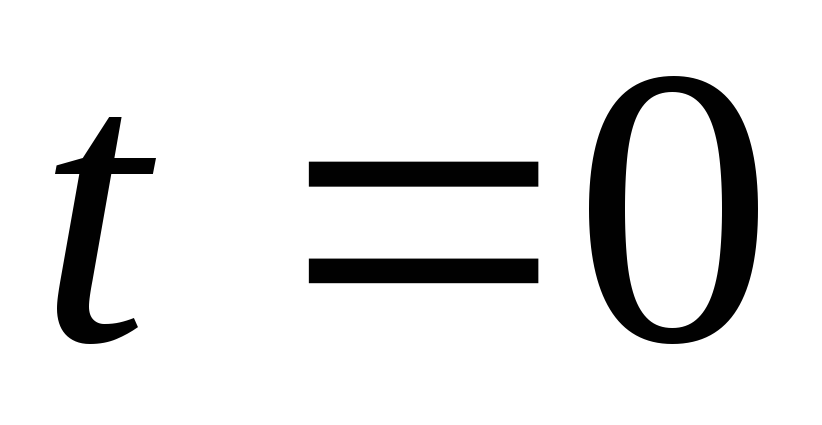и подставив значения начальных токов и напряжений, определим первые производные в момент коммутации.

Продифференцировав эти уравнения и подставив значения первых производных, получим значения вторых и т.д.

Пример:

а)

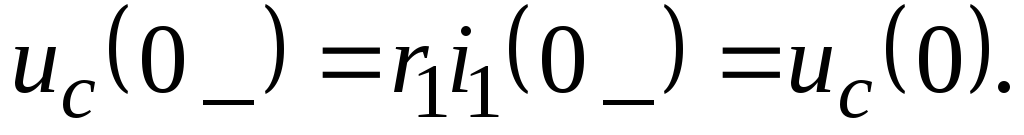
б)

схема замещения для будет:

. Классический метод расчета переходных процессов .

8.6 Принужденный и свободный режимы

В общем случае анализ п/пр в ЛЭЦ с сосредоточенными параметрами , сводится к решению обыкновенных дифференциальных уравнений, выражающих законы Кирхгофа.

Например, если к какой-либо цепи, состоящий из последовательно соединенныхто интегро-дифференциальное уравнение имеет вид:

Это уравнение после дифференцирования приводится к неоднородному дифференциальному уравнению второго порядка

Как известно, общее решение такого уравнения равно сумме частного решения неоднородного уравнения и общего решения однородного уравнения :

полный ток, где

–частное решение дифференциального с известной правой частью выражает принужденный режим,

–общее решение соответствующего однородного уравнения, которое получают положив правую часть равной нулю, выражает свободный режим. Однородное уравнение будет:

Соответствующее ему характеристическое уравнение

решая его, находим корни ,. Тогда общее решение запишется в виде:

Где ,постоянные интегрирования, которые определяются из начальных условий.

Свободные составляющие токов и напряжений зависят только от внутренних запасов энергии электрических и магнитных полей и не зависит от внешних источников.

С течение времени , тогда. Если воздействующая функция, стоящая в правой части уравнения, постоянна или является периодической функцией времени, то принужденный ток будет одновременно и установившимся–определяется действием только внешних источников.

Таким образом, при классическом методе расчета п/пр разбивается на два процесса : принужденный, обусловленный действием источников, и свободный, обусловленный внутренними запасами энергии электрических и магнитных полей.

Порядок расчета переходных процессов классическим методом.

1. Определяет НУ до коммутации

2. Для после коммутационной схемы составляется система уравнений по законам Кирхгофа. Эти уравнения сводятся к одному относительно искомого тока или напряжения.

3. Записываем искомое решение в виде ;

4. Находим . Цепь рассчитывается каким-либо методом постоянного тока, если цепь находится под воздействием постоянного источника, или комплексным методом, если цепь находится под воздействием переменного тока.

5. Записывается характеристическое уравнение и находятся его корни

6. 

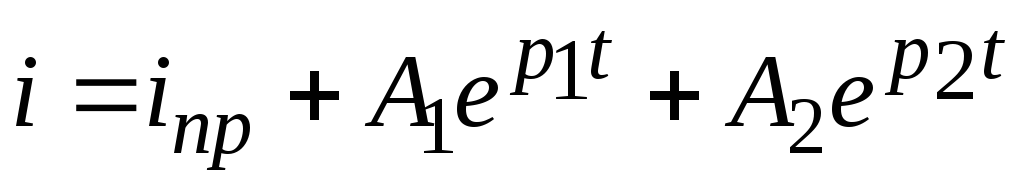
7. Находим постоянные интегрирования ,для чего получаем:

8. Записываем окончательный результат