19. Функция эластичности

Функция эластичности

Эластичность показывает как изменится спрос с любым небольшим относительным изменением цены. Обозначается

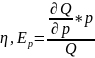
Определение Для данного Q спрос называется: 1) эластич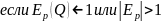ным, ; 2)неэластичным, ; 3)единичная эластичность

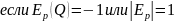
Производитель получается

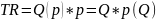
Total revenue

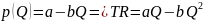
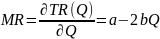
– функция предельного дохода

Теорема Если функция строга линейна, то функция предельного дохода также линейна, имеет ту же точку пересечения с осью ординат, но ее наклон относительно этой оси меньше в 2 раза, чем у кривой спроса.

Доказательство

Теорема

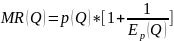
Доказательство

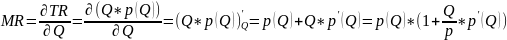
Потребительский излишек(CS – consumer surplus)

-Это мера благосостояния, характеризующая выигрыши благосостояния товара при открытии рынка товара. Чтобы его посчитать, необходимо найти площадь заштрихованного треугольника на рисунке.

; ;

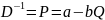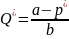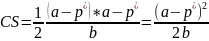
20. Рыночные структуры

21. Совершенная конкуренция

Покупатель или продавец называется конкурирующим, а его поведения называется совершенно конкуреynysv, если он предполагает или считает, что рыночная цена является заданной и что его действия не могут на нее повлиять.

Кооперативные игры

N={1,2,3,…,n}

Кооперативная игра – отображение множества из множества всех подмножеств?!

V: 2^N->R, V(ᴓ)=0

V[S] ∊R – способ множества (коалиции) зарабатывать

V∊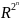 – вектор из кол-ва чисел 2^N, при котором одно из них равно 0

Ядро – множество данных Х=(х1,х2,…,хn) ∊ R^N таких, что 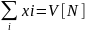, а также для ∀ S N

Ядро – выпуклый многогранник в множестве R^N

Вектор Шепли (Sh)

n! – возможность посмотреть n человек по одному и дополнительно друг к другу

Sh= 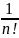< ∑ дележей>

Возможны следующие случаи:

1. Ядро м.б пустым (находим вектор Шепли

2. ядро м.б не пустым и вектор Sh∊ ядру (находится внутри ядра) «хорошая игра»

3. ядро м.б не пустым, но вектор Шепли находится не в ядре «плохая игра»

Супермодулярные кооперативные игры

Sh=(ϕ1(ν), ϕ2(ν), …, ϕn(ν))

ϕi(ν)=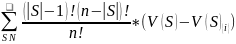

k=|S|- размер коалиции

(V(S)-V(S)_{i}) – вклад i-го игрока в коалицию

Вектор Шепли – единственный делёж, который:

1. симметричен

ϕi(ν)= ϕj(ν) – для симметричных игр.

Определение:

2 игрока симметричны, если присоединение любого из игроков к коалиции S одинаково усилит эту коалицию

∀ S N|_{i,j}=>V[S˽i]-V[S˽i]

2. аддитивен, т.е для 2х игр

G= <N,ν> и G=<N,ω> и ∀i∊N справедливо равенство

ϕj(ν+ ω)= ϕi(v)+ ϕ(ω)

3. назначает ϕi(ν)=0 нулевым игрока i∊N (назначает нулевой выигрыш нулевым игрокам)

22. Кооперативные игры

Определение:

Игрок нулевой, если его присоединение к коалиции дает нулевой выигрыш

i – нулевой, если ν (S˽i)= ν (S) ∀S∊N

Определение:

Следующие 2 свойства 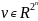(вектор v длинной 2^N из действительных чисел) эквивалентны

1. Для ∀ игрока i∊N, ∀T S N, i∊S => ν[S˽i]- v[S] ≥ V[T˽i] – V[T]

Игроки приносят больший выигрыш при подключении к большей коалиции

2. ∀ S,T N, v[SᴗT]+v[SᴖT]≥v[S]+v[T]

Игра, обладающая 1 и 2 свойствами называется супермодулярной

Теорема о CMD

⊐v – SMD=>∀ упорядочивания игроков σ∊Sn – дележ Шепли для упорядочивания σ ∊ ядру

Следствие

Эти дележи порождают ядро => ядро игры является выпуклой n! этих дележей