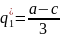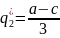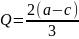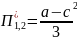Теория игр
Существует несколько типов игр в экономике
Статические с полной информацией
Динамические с полной информацией
Статические с неполной информацией
Динамические с неполной информацией
Игры с полной информацией
Игроки принимают решения (делают выбор стратегии) независимо друг от друга и одновременно. Функции выигрышей всех игроков известны (всем игрокам). Игру можно представить в нормальной и экстенсивной форме. Нормальная форма игры определяет игроков, стратегии доступные любому игроку, выигрыши каждого игрока для каждой комбинации стратегий, которая может быть выбрана всеми игроками.
Пусть в игре участвует n игроков, Si – множество всех стратегий доступных i-му игроку. si ∈Si – элемент множества стратегий, (s1, s2, …, sn) – комбинация стратегий, Ui (s1, s2, …, sn) – функция выигрыша игрока i.
Нормальная форма игры с n игроками определяет множество стратегий всех игроков S1, S2, …, Sn и функции выигрыша для каждого игрока U1, U2, …, Un.
G = {S1, S2, …, Sn, U1, U2, …, Un}
Рассмотрим игру с n игроками в нормальной форме. Пусть si’, si’’ ∈ Si – достижимые стратегии для игрока i.
Стратегия si’ строго доминируется стратегией si’’ если, для любых комбинаций стратегий других игроков, выигрыш игрока i, если он играет стратегию si’, строго меньше, чем если бы он играл стратегию si’’.
Ui(s1, s2, …, si-1, si’, si+1, …, sn) < Ui(s1, s2, …, si-1, si’’, si+1, …, sn) Для любых (s1, s2, …, si-1, si+1, …, sn)
Дилемма заключенного
Говорить
Молчать
Говорить
(-5, -5)
(0,-10)
Молчать
(-10,0)
(-1,-1)
Равновесие Нэша
Рассмотрим игру в нормальной форме G = {S1, S2, …, Sn, U1, U2, …, Un}
Стратегии (s1*, s2*, … , sn*) образуют равновесия Нэша, если для любого игрока i, стратегия si*это наилучший ответ игрока i (обозначается best response) на стратегии (s1*, s2*, …, si-1*, si+1*, …, sn*) остальных (n-1) игроков.
Ui(si*, s-i*) ≥ Ui(si, s-i*) для любой достижимой стратегии si игрока i.
Т.е. решение оптимизационной задачи
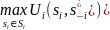
Утверждение 1. Рассмотрим игру для n игроков в нормальной форме. Представим, что в игре путем исключения доминируемых стратегий, мы исключили все стратегии кроме (s1*, s2*, … , sn*). Тогда эти стратегии являются единственным равновесием Нэша в данной игре.
Утверждение 2. Рассмотрим игру в нормальной форме с n игроками. Если стратегии (s1*, s2*, … , sn*) являются равновесием Нэша, то они «выживут» при исключении доминируемых стратегий (но решения таким путем может и не существовать).
Дуополия курно
i=1,2.
Q=q1+q2 (объем)
P(Q)=a-Q (цена)
ci(qi)=cqi (общие издержки фирмы i на продукцию
Предельные издержки постоянны (чем больше производим, тем больше нам требуется).
Нормальная форма игры. Стратегия Si = [0;+∞) выпустить продукцию от 0 до +∞. Ui=Пi.
G = { Si = [0;+∞), Ui=Пi} i=1,2.
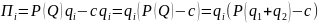
Si=qi (стратегия это то количество продукции, которое нужно произвести)
Для
любого i
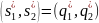будет равновесием Нэша, тогда и только
тогда, когда
т.е.
и
У
нас
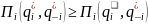
Решаем максимизационную задачу
Для 1 фирмы
BR1(q2)
Для 2 фирмы
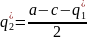BR2(q1)
