
1 Тепловое излучение. Тепловое излучение (радиационный теплообмен) – способ передачи теплоты за счет распространения электромагнитных волн в определенном диапазоне частот. Все тела с температурой выше 0 К обладают собственным тепловым излучением. Лучистая энергия может передаваться и в вакууме.
Спектром
излучения
называют распределение лучистой энергии
по дине волны
 ,
где
,
где
 ,
Вт/м3
спектральная лучеиспускательная
способность тела.
,
Вт/м3
спектральная лучеиспускательная
способность тела.
 – поглощательная способность тела,
равная доле падающего излучения
поглощенного телом;
– поглощательная способность тела,
равная доле падающего излучения
поглощенного телом;
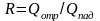 – отражательная способность тела,
равная доле падающего излучения
отраженного телом;
– отражательная способность тела,
равная доле падающего излучения
отраженного телом;
 – пропускательная способность
тела, равная доле падающего излучения
проходящего через тело.
– пропускательная способность
тела, равная доле падающего излучения
проходящего через тело.
Плотность потока собственного излучения или лучеиспускательная способность тела:
 или
или
 .
.
Эффективный
тепловой поток равен:
 .
.
Результирующий
тепловой поток: .
.
Основной закон излучения – закон Стефана–Больцмана:
 ,
,
где Е0 – лучеиспускательная способность абсолютно черного тела (АЧТ), Вт/м2; 0 = 5,6710-8 Вт/(м2К4) – постоянная Стефана–Больцмана; Т – температура поверхности абсолютно черного тела, К.
2 Температурное поле - это совокупность значений температуры во всех точках данной расчетной области и во времени.
В зависимости от числа координат различают трехмерное, двумерное, одномерное и нульмерное (однородное) температурные поля.
Температурное поле, которое изменяется во времени, называют нестационарным температурным полем. И наоборот, температурное поле, которое не изменяется во времени, называют стационарным температурным полем.
Примеры записи температурных полей: T(x,y,z,τ) – трехмерное нестационарное температурное поле (τ – время); T(τ) – нульмерное нестационарное температурное поле; T(x) – стационарное одномерное температурное поле; T = const – нульмерное стационарное температурное поле.
3 Теплообменные аппараты. Для теплового расчета рекуперативного теплообменника используют два основных уравнения – уравнение теплового баланса и уравнение теплопередачи. Без учета тепловых потерь в теплообменном аппарате уравнение теплового баланса имеет вид:
 ,
,
где
 – количество теплоты, отдаваемое горячим
теплоносителем в единицу времени, Вт;
– количество теплоты, отдаваемое горячим
теплоносителем в единицу времени, Вт;
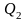 – количество теплоты, воспринимаемое
холодным теплоносителем в единицу
времени, Вт. В развернутом виде уравнение
теплового баланса можно записать:
– количество теплоты, воспринимаемое
холодным теплоносителем в единицу
времени, Вт. В развернутом виде уравнение
теплового баланса можно записать:
а) для однофазных теплоносителей
 ;
;
б) при изменении агрегатного состояния горячего теплоносителя (горячий теплоноситель – влажный насыщенный водяной пар)
 ,
,
где G1
и G2 – массовые
расходы горячего и холодного теплоносителей,
кг/с; cp1
и cp2
– удельные массовые изобарные теплоемкости
горячего и холодного теплоносителей,
Дж/(кгК);
 и
и
 – температуры горячего теплоносителя
на входе и выходе из теплообменника,
°С;
– температуры горячего теплоносителя
на входе и выходе из теплообменника,
°С;
 и
и
 – температуры холодного теплоносителя
на входе и выходе из теплообменника,
°С; x – степень сухости
пара.
– температуры холодного теплоносителя
на входе и выходе из теплообменника,
°С; x – степень сухости
пара.
Расходы теплоносителей рассчитывают по уравнению неразрывности:
 ,
,
При поперечном обтекании трубы на лобовой части ее поверхности образуется ламинарный пограничный слой, толщина которого постепенно увеличивается (рис. 11-13). При обтекании лобовой части трубы сечение потока уменьшается, скорость жидкости увеличивается, а давление у по поверхности падает. В кормовой части трубы давление увеличивается, гик как скорость уменьшается; скорость жидкости в пограничном Слое также снижается, а начиная с некоторого сечения частицы движутся в обратном направлении, образуя вихри, которые периодически отрываются с поверхности трубы и уносятся потоком (подробнее см. разд. 6.8). При этом соответственно изменяется значение локального коэффициента теплоотдачи по поверхности (окружности) трубы (рис. 11-13, в, г).
Р ис.
11-13. Схема поперечного обтекания трубы
теплоносителем:
ис.
11-13. Схема поперечного обтекания трубы
теплоносителем:
А — при ламинарном пограничном слое; б — при турбулентном пограничном слое; в — распределение скорости у поверхности трубы; г-изменение локального коэффициента теплоотдачи по ПоверхНости цилиндра (1 — Re = 70 800; 2 — Re = 219000)
Максимальное
значение ![]() лобовой
образующей трубы (угол
лобовой
образующей трубы (угол ![]() =0),
где толщина пограничного слоя
=0),
где толщина пограничного слоя ![]() Г
мала. Затем коэффициент теплоотдачи
снижается за счет увеличения
Г.
Такой режим наблюдается при Re до 2-105.
При дальнейшем увеличении числа
Рейнольдса (при Re>2-105) ламинарный
пограничный слой переходит в турбулентный,
и точки отрыва перемещается в кормовую
сторону трубы.
Г
мала. Затем коэффициент теплоотдачи
снижается за счет увеличения
Г.
Такой режим наблюдается при Re до 2-105.
При дальнейшем увеличении числа
Рейнольдса (при Re>2-105) ламинарный
пограничный слой переходит в турбулентный,
и точки отрыва перемещается в кормовую
сторону трубы.
Локальный коэффициент теплоотдачи при этом может иметь два минимальных значения (рис. 11-13,г): одно — в точке перехода ламинарного пограничного слоя в турбулентный, другое — в точке отрыва от поверхности трубы турбулентного пограничного слоя, Для определения среднего коэффициента теплоотдачи при поперечном обтекании трубы предложены следующие уравнения:
При
Re=5- ![]()
Nu=0,5Re0,5Pr0,38(Pr/Prcт)0,25; (11.66)
При Re=103 – 2*105
Nu=0,25Re0,6Pr°,43(Pr/Prcт)0,25. (11.67)
4. КОНВЕКТИВНЫЙ ТЕПЛООБМЕН - необратимый процесс переноса теплоты в движущихся средах с неоднородным полем темп-ры, обусловленный совместным действием конвекции и молекулярного движения.
Наиб. важный для практики случай - К. т. между движущейся средой и поверхностью её раздела с др. средой (твёрдым телом, жидкостью или газом) - наз. конвективной теплоотдачей. Вследствие вязкости движущейся среды она "прилипает" к поверхности раздела, в результате местная скорость среды относительно этой поверхности равна нулю. Поэтому плотность конвективного теплового потока, подходящего к поверхности раздела (или отходящего от неё), может быть описана с помощью закона теплопроводности (закона Фурье):
![]()
где ![]() -
коэф. молекулярной теплопроводности, Т -
темп-pa среды. Если
-
коэф. молекулярной теплопроводности, Т -
темп-pa среды. Если ![]() характеризует
физ. свойства среды, то градиент темп-ры
формируется под действием конвективного
движения среды.
характеризует
физ. свойства среды, то градиент темп-ры
формируется под действием конвективного
движения среды.
ГЛАВА ТРЕТЬЯ. ТЕПЛООБМЕН В ЖИДКОСТЯХ И ГАЗАХ
5 Теплоотдача при обтекании плоской поверхности (пластины)
1. Гидродинамические
условия развития процесса. При продольном
течении жидкости вдоль
плоской поверхности происходит
образование динамического пограничного
слоя, в пределах которого вследствие
сил вязкого трения скорость
изменяется от значения скорости
невозмущеиного потока ![]() на
внешней границе слоя до нуля на самой
поверхности пластины. По мере движения
потока вдоль поверхности толщина
пограничного слоя постепенно возрастает;
тормозящее воздействие стенки
распространяется на все более далекие
слои жидкости. На небольших расстояниях
от передней кромки пластины пограничный
слой весьма тонкий и течениежидкости в
нем носит струйный ламинарный характер.
Далее, на некотором расстоянии
на
внешней границе слоя до нуля на самой
поверхности пластины. По мере движения
потока вдоль поверхности толщина
пограничного слоя постепенно возрастает;
тормозящее воздействие стенки
распространяется на все более далекие
слои жидкости. На небольших расстояниях
от передней кромки пластины пограничный
слой весьма тонкий и течениежидкости в
нем носит струйный ламинарный характер.
Далее, на некотором расстоянии ![]() в
пограничном слое начинают возникать
вихри и течение принимает турбулентный
характер. Вихри обеспечивают интенсивное
перемешивание жидкости в пограничном
слое, однако в непосредственной близости
от поверхности они затухают и здесь
сохраняется очень тонкий вязкий подслой.
Описанная картина развития процесса
показана на рис. 3-1.
в
пограничном слое начинают возникать
вихри и течение принимает турбулентный
характер. Вихри обеспечивают интенсивное
перемешивание жидкости в пограничном
слое, однако в непосредственной близости
от поверхности они затухают и здесь
сохраняется очень тонкий вязкий подслой.
Описанная картина развития процесса
показана на рис. 3-1.

Рис. 3-1. Схема движения жидкости при обтекании пластины.
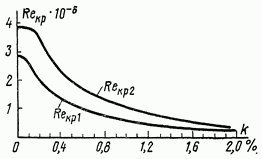
Рис. 3-2. Зависимость критического числа Re от степени турбулентности потока.
Толщина
пограничного слоя 6 зависит от расстояния
от передней кромки пластины, скорости
потока ![]() и
кинематического коэффициента вязкости
v. При ламинарном пограничном слое
и
кинематического коэффициента вязкости
v. При ламинарном пограничном слое

При турбулентном пограничном слое
![]()
где ![]() —
число Рейнольдса, в котором в качестве
характерного оазмеоа поинято оасстояние
х.
—
число Рейнольдса, в котором в качестве
характерного оазмеоа поинято оасстояние
х.
Переход к турбулентному режиму течения жидкости в пограничном слое определяется критическим значением числа Рейнольдса:
![]()
которое при
продольном обтекании пластины обычно
принимают равным ![]() .
.
Более подробный
анализ показывает, что величина ![]() зависит
от ряда факторов. Основное влияние
оказывает степень начальной турбулентности
набегающего потока, т. е. наличие в потоке
начальных возмущений и завихрений.
Степень турбулентности потока принято
характеризовать отношением величины
средней скорости турбулентных
пульсаций
зависит
от ряда факторов. Основное влияние
оказывает степень начальной турбулентности
набегающего потока, т. е. наличие в потоке
начальных возмущений и завихрений.
Степень турбулентности потока принято
характеризовать отношением величины
средней скорости турбулентных
пульсаций ![]() к
скорости движения потока
к
скорости движения потока ![]() ,
т. е. коэффициентом
,
т. е. коэффициентом ![]() .
Чем выше начальнаятурбулентность потока,
тем меньше величина
.
Чем выше начальнаятурбулентность потока,
тем меньше величина ![]() .
Средняя скорость пульсаций в потоке
определяется как
.
Средняя скорость пульсаций в потоке
определяется как

где ![]() —
мгновенное значение вектора пульсационной
скорости;
—
мгновенное значение вектора пульсационной
скорости; ![]() —
осреднепное во времени значение
квадрата
—
осреднепное во времени значение
квадрата ![]() .
.
Кроме того,
на величину ![]() может
влиять шероховатость поверхности
пластины, интенсивность теплообмена и
т. д. Сам переход от ламинарного к
турбулентному режиму течения жидкости в
пограничном слое, как показывают опытные
данные, происходит не в точке, а на
некотором участке, в связи с чем иногда
вводят два значения:
может
влиять шероховатость поверхности
пластины, интенсивность теплообмена и
т. д. Сам переход от ламинарного к
турбулентному режиму течения жидкости в
пограничном слое, как показывают опытные
данные, происходит не в точке, а на
некотором участке, в связи с чем иногда
вводят два значения: ![]() ,
где
,
где ![]() —
критическое число Рейнольдса, отвечающее
переходу от ламинарного к переходному
режиму течения, когда в пограничном
слое возникают первые вихри и пульсации;
—
критическое число Рейнольдса, отвечающее
переходу от ламинарного к переходному
режиму течения, когда в пограничном
слое возникают первые вихри и пульсации; ![]() —
критическое число Рейнольдса для
перехода к развитому турбулентному
режиму течения. На рис. 3-2 приведены
зависимости
—
критическое число Рейнольдса для
перехода к развитому турбулентному
режиму течения. На рис. 3-2 приведены
зависимости ![]() от
степени начальной турбулентности набегающего
потока.
от
степени начальной турбулентности набегающего
потока.
Впервые
теоретический расчет распределения
скоростей в ламинарном пограничном
слое выполнил Г. Блазиус в 1908 г. Он
установил, что отношение скоростей ![]() зависит
только от одной переменной
зависит
только от одной переменной ![]() ,
т. е. профиль скорости в пограничном
слое имеет вид:
,
т. е. профиль скорости в пограничном
слое имеет вид:
![]()
График этого
профиля показан на рис. 3-3. Хотя строго
теоретически ![]() стремится
к значению
стремится
к значению ![]() лишь
асимптотически, из рис. 3-3 видно, что уже
при значении
лишь
асимптотически, из рис. 3-3 видно, что уже
при значении ![]() различие
между w и
различие
между w и ![]() практически
исчезает (точнее, при
практически
исчезает (точнее, при ![]() ).
Это значение
).
Это значение ![]() определяет
расстояние
определяет
расстояние ![]() ,
принимаемое обычно за
толщинуламинарного пограничного
слоя; отсюда следует формула
(3-1).
,
принимаемое обычно за
толщинуламинарного пограничного
слоя; отсюда следует формула
(3-1).
Поток, обтекающий пластину, оказывает на нес определенное динамическое воздействие. Последнее проявляется в форме силы, приложенной к поверхности пластины и направленной по касательной к ней в сторону движения жидкости.
Такая касательная сила, отнесенная к единице поверхности пластины, называется касательным напряжением тления и определяется согласно закону вязкого трения Ньютона как

Производная ![]() с
учетом зависимости (3-3) может быть
записана
с
учетом зависимости (3-3) может быть
записана

так как из рис. 3-3 видно, что
![]()

Рис. 3-3. Распределение скоростей при ламинарном режиме течения в пограничном слое.
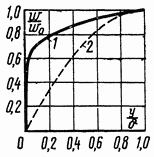
Рис. 3-4. Распределение скоростей в пограничном слое в относительных координатах. 1 — турбулентный режим течения; 2 — ламинарный режим течения.
