Квантовая физика

1. Гипотеза де Бройля

Гипотеза де Бройля заключается в том, что французский физик Луи де Бройль выдвинул идею приписать волновые свойства электрону. Проводя аналогию между квантом, де Бройль предположил, что движение электрона или какой-либо другой частицы, обладающей массой покоя, связано с волновым процессом.

Гипотеза де Бройля устанавливает, что движущейся частице, обладающей энергией E и импульсом p, соответствует волновой процесс, частота которого равна:

а длина волны:

где p - импульс движущейся частицы.

2. Физический смысл волновой функции. Плотность вероятности.

Физический смысл волновой функции. Величина |psi(x,y,z,t)|2dV пропорциональна вероятности того, что частица будет обнаружена в момент времени t в объеме dV в окрестности точки (x,y,z).

Волновая функция системы невзаимодействующих частиц psi(r1,r2,...rn,t) связана с одночастичными волновыми функциями psii(ri,t) соотношением

psi(r1,r2,...rn,t) = psi1(r1,t)·psi2(r2,t)·...psin(rn,t).

Функция - производная функции распределения – характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения (иначе – «плотность вероятности») непрерывной случайной величины.

3. Какими свойствами должны обладать операторы, чтобы они изображали физические величины?

В квантовой механике используются линейные операторы, т.е. операторы, обладающие свойствами:

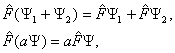  (15)

где , - произвольные функции, а - произвольная постоянная. Оператор физической величины должен обладать еще одним свойством: он должен быть эрмитовым (самосопряженным). По определению, оператор  называется эрмитовым , если

  , (16)

т.е.  , где 

  -

матричный элемент оператора .

Покажем, что свойство эрмитовости обеспечивает вещественность среднего значения физической величины. С этой целью вычислим величину, комплексно сопряженную к величине (14):

(если оператор  эрмитов, то  и поэтому)

  ,

что и требовалось доказать. Здесь - оператор, транспонированный к оператору , определяемый равенством

   

где  и  - произвольные функции.

 Часто используют обозначение: , оператор  называется эрмитовосопряженным по отношению к оператору . Если оператор  эрмитов, то .

 В классической механике компоненты радиуса-вектора и вектора импульса частицы подчиняются коммутативному закону умножения. Например, . Проверим, выполняется ли этот закон для операторов физических величин. Вычисляем:

 

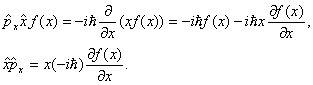
Значит,

  .

Величина  называется коммутатором операторов  и . Если , то говорят, что операторы  и  коммутируют друг с другом.

Введём оператор отклонения физической величины от среднего значения (оператор абсолютной погрешности, или оператор флуктуации физической величины): .

Это эрмитовый оператор, если только оператор  эрмитовый. Поскольку , то в качестве меры отклонения величины от среднего значения можно взять среднее квадратичное отклонение  . Вычислим эту величину:

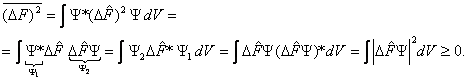  (17)

Как видим, среднее квадратичное отклонение всегда неотрицательно.