
- •1) Залежно від реєстрації фактів ряди динаміки бувають дискретними і неперервними.
- •Фактичний обсяг щомісяччних податкових надходжень пдфо до Приморської дпі м. Одеси за роками, тис.Грн.
- •Скоригований обсяг щомісячних податкових надходжень пдфо до Приморської дпі м. Одеси за роками, тис.Грн.
- •3. Побудуємо динаміку за скоригованими щомісячними надходженнями пдфо і визначимо тренд. Для наочності представимо це графічно.
- •Прогнозування обсягів щомісячних податкових надходжень з пдфо до Приморської дпі м.Одеси з липня по грудень 2009 року
- •7. Метод експоненційного згладжування
- •Результати пошуку на сітці
- •Результати прогнозування за допомогою експоненційного згладжування
Скоригований обсяг щомісячних податкових надходжень пдфо до Приморської дпі м. Одеси за роками, тис.Грн.
Рік
Місяць |
2005 |
2006 |
2007 |
2008 |
2009 |
Січень (1) |
5534,851 |
9275,541 |
16054,35 |
25952,08 |
26221,6 |
Лютий (2) |
10776,54 |
14201,67 |
25146,25 |
37103,9 |
36502,2 |
Березень (3) |
14329,66 |
17875,31 |
25973,56 |
43586,59 |
40670,2 |
Квітень (4) |
15119,35 |
18352,04 |
30208,13 |
40329,36 |
37519,9 |
Травень (5) |
9714,172 |
15058,55 |
29634,91 |
39062,71 |
34799,5 |
Червень (6) |
14532,81 |
20709,56 |
33817,24 |
45030,08 |
41807,8 |
Липень (7) |
17896,81 |
18416,93 |
35841,91 |
41162,85 |
37059 |
Серпень (8) |
13251,97 |
16723,25 |
33931,27 |
34430,67 |
32204,4 |
Вересень (9) |
14355,91 |
19258,35 |
32030,18 |
41258,21 |
|
Жовтень (10) |
13558,17 |
19360,68 |
35201,08 |
43285,47 |
|
Листопад (11) |
15755,69 |
19912,03 |
37725,91 |
38111,36 |
|
Грудень (12) |
24752,67 |
31264,38 |
40115,253 |
49990,46 |
|
Середньомісячні |
14131,55 |
18367,36 |
32501,52 |
39941,98 |
|
3. Побудуємо динаміку за скоригованими щомісячними надходженнями пдфо і визначимо тренд. Для наочності представимо це графічно.

Рис. 2. Динаміка скоригованих щомісячних надходжень ПДФО до Приморської ДПІ м.Одеси за 2005-2009 роки, тис.грн.
На основі графічного зображення динамічного ряду надходжень ПДФО та побудови лінії тренду можна зробити ряд висновків:
- наявність лінійного тренду (тобто основну тенденцію зміни часового ряду, яка описується часовою функцією f(t)).
Тренд описується функцією часу: f(t)=661,36t+8895,7 з коефіцієнтом детермінації R2 =0,7999;
- присутність певної сезонності (сезонні коливання St),
- відсутність аномальних значень (так звані «випади» в коливанні et («білий шум»)), вони візуально не порушують уявлення про властивий даному динамічному ряду тренд.
4. Для будь-якого динамічного ряду характерною властивістю є залежність рівнів: значення yt залежить від попередніх значень: yt-1, yt-2 і т.д. Для оцінювання ступенів залежності рівнів ряду використовують коефіцієнти автокореляції rр з часовим лагом р = 1,2…m, які характеризують щільність зв’язку між первинним рядом і цим же рядом, зсуненим на р моментів.
Значення коефіцієнта автокореляції rp визначається величиною лага р та не виходить за межі +-1.
 (4)
(4)
Послідовність коефіцієнтів rp називають автокореляційною функцією (АКФ) і зображують графічно у вигляді автокорелограми з абсцисою р та ординатою rp. На графіку зазвичай позначаються 2 паралельні прямі, які визначають 95%-ві довірчі межі істотності rp. Якщо rр не виходить за довірчі межі, то ряд вважається стаціонарним.
За швидкістю згасання АКФ можна зробити висновок про характер динаміки. Найчастіше використовується значення r1. Характеризуючи ступінь залежності двох послідовних членів ряду, коефіцієнт автокореляції є мірою неперервності цього ряду. Якщо r1 1, то ряду динаміки властива тенденція розвитку. Якщо r1 0, то рівні ряду незалежні. Відносно високі значення коефіцієнта автокореляції при р=k, 2k, 3k свідчать про регулярні коливання.
Основними інструментами ідентифікації порядка АРПСС моделі є графіки автокореляційної функції (АКФ) та часткової автокореляційної функції. Побудуємо автокореліційну функцію за виправленими значеннями щомісячних надходжень ПДФО за роками (залежність кожного наступного рівня від попереднього).
 Рис.
3. Автокореляційна функція щомісяччних
надходжень ПДФО до Приморської ДПІ
м.Одеси за 2005-2009 роки.
Рис.
3. Автокореляційна функція щомісяччних
надходжень ПДФО до Приморської ДПІ
м.Одеси за 2005-2009 роки.
Проаналізувавши графік, можна стверджувати наявність автокореляції і вплив кожного попереднього значення на наступне, адже всі значення виходять за довірчий інтервал, який позначено штрихами. Коефіцієнт кореляції rp змінюється від 0,778 до 0,195 з лагом 1 при 15 досліджуваних значеннях. Останнє значення (15) знаходиться у межах довірчого інтервалу, що свідчить про відсутність залежності. Якщо rр не виходить за довірчі межі, то ряд вважається стаціонарним, але в даному випадку ряд є нестаціонарним, що буде підтверджено далі.
Продовжимо дослідження і припустимо наявність залежності з лагом = 2.
Побудуємо часткову автокореляційну функцію для визначення чи є ще більша залежність при зрушенні на 2 одиниці.
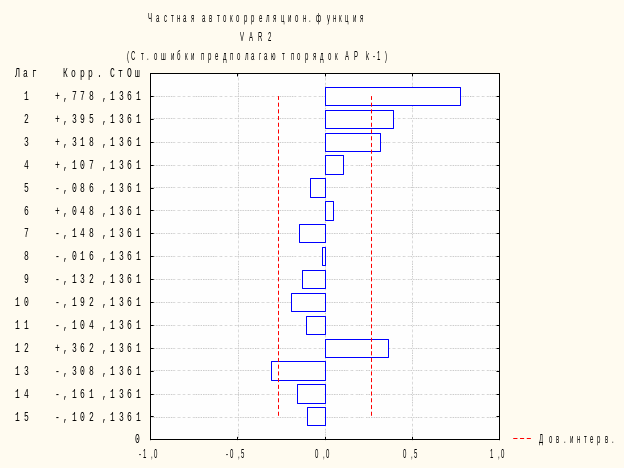 Рис.
4. Часткова автокореляційна функція
щомісячних надходжень ПДФО до Приморської
ДПІ м.Одеси за 2005-2009 роки.
Рис.
4. Часткова автокореляційна функція
щомісячних надходжень ПДФО до Приморської
ДПІ м.Одеси за 2005-2009 роки.
Оцінивши графік, можна прийти до висновку, що часткова автокореляція при значенні лагу 2 відсутня.
Спостерігається сезонна компонента з даного графіку, яка становить 12 з лагом 12, надходження ПДФО найбільше здійснюється в кінці кожного року.
5. Перевіримо наявність сезонної складової та її лаг за допомогою Excel. Для цього побудуємо графіки для кожних 12 місяців (6, 3, 4…) за 2005-2009 роки.. Оскільки часткова автокореляційна функція дала приблизне значення сезонності в 12 місяців, то побудуємо графіки ПДФО за 12 місяців. (Крім того, основна частина ПДФО надходить до бюджету щомісячно, а остаточна сума податку надходить в кінці кожного року, тому в грудні спостерігається найбільший обсяг податкових надходжень)

Рис. 5. Динаміка щомісячних податкових надходжень ПДФО до Приморської ДПІ м.Одеси, зображена за роками (2005-2009 роки), тис. грн.
Побудувавши динаміку ПДФО за роками бачимо підтвердження результатів часткової автокореляційної функції, що свідчить про наявність сезонної компоненти з порядком 12 (лаг=12). ПДФО надходить до бюджету з деяким темпом росту щомісячно, але остаточна сума податкових надходжень за даним податком спостерігається у кінці року.
6. Таку динаміку, яку ми спостерігаємо по щомісячних надходженнях ПДФО до Приморської ДПІ м.Одеси за 2005-2009 роки описує модель ARIMA*ARIMAS із сезонним лагом 12.
Параметри ARIMA*ARIMAS:
р – параметр авторегресії (регулярний)
Р – сезонний параметр авторегресії
q – параметр ковзної середньої (регулярний)
Q – сезонний параметр ковзної середньої
Необхідно вказати хоча б один із зазначених параметрів.
Найпростіші види моделей ARIMA*ARIMAS такі:
(1,0,0) – авторегресійна функція
(0,0,1) – ковзна середня
(1,0,1) – комбінована модель авто регресії та ковзної середньої
(0,1,1) – експоненційна середня
(1,1,1) – нестаціонарний процес з лінійним трендом
(0,1,1)* (0,1,1) – мультиплікативна модель сезонного процесу.
Практична реалізація моделей можлива лише на рядах довжиною не менше 50 спостережень.
Модель ARIMA*ARIMAS має такий вигляд:
yt = pt-1yt-1 + a + bt – qt-1et-1 (5)
yt – рівні ряду динаміки у момент часу t = 1, 2… 54
f(t) = a + bt - трендова комнонета
pt-1 – коефіцієнт авто регресії першого порядку
qt-1 – коефіцієнт моделі ковзного середнього
et-1 – іррегулярна компонента (випадкові відхилення або «білий шум»)
Для знаходження сезонних коефіцієнтів застосовувалось згладжування ковзного середнього першого порядку: St = c + Qt-1St-1 (6)
Параметри моделі оцінювалися з 95% рівнем довіри, тобто з 5% рівнем ризику.
До того, як почати оцінювання, необхідно вирішити, який тип моделі буде підбиратися до даних, і яка кількість параметрів присутня в моделі, іншими словами, потрібно ідентифікувати модель АРПСС. Основними інструментами ідентифікації порядку моделі є графіки, автокореляційна функція (АКФ), приватна автокореляційна функція (ЧАКФ).
Вид моделі ARIMA, адекватність її реальному процесу та прогнозні властивості залежать від порядку авторегресії р та порядку ковзної середньої q Через те ключовим моментом моделювання вважається процедура ідентифікації – обґрунтування виду моделі. В стандартній методиці ідентифікація зводиться до візуального аналізу автокорелограм і ґрунтується на принципі економії, за яким (р + q)<=2.
Перш за все, для побудови та ідентифікації моделі визначимо, чи є ряд стаціонарним. Для цього побудуємо графік різниць.
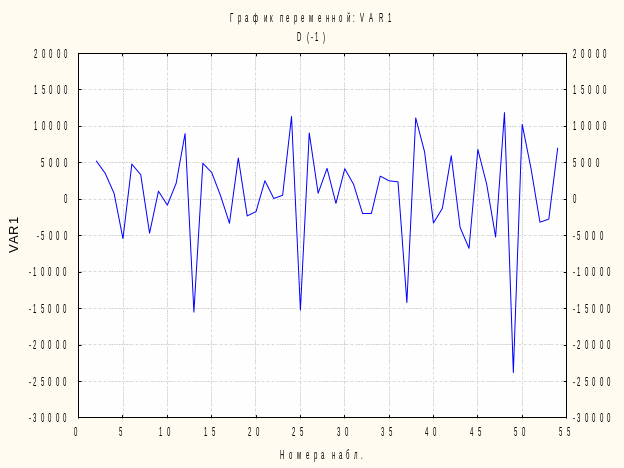 Рис.
6. Графік різниць
Рис.
6. Графік різниць
Після взяття різниць з лагом = 1 графік свідчить про те, що динаміка не наближається до 0, отже, ряд є нестаціонарним і потребує згладжування, що було підтверджено також частковою атокореляційною функцією.
Це прослідковується і на першому графіку, так як ми маємо зростаючий тренд і відповідно зростання коливань навколо 0.
За даними автокореляційної функції бачимо, що значення виходять за межі довірчого інтервалу, та графіку різниць, значення якого не наближається до 0, свідчить, що ряд є нестаціонарним.
Значення буде q = 1, Q(s) = 1 за принципом мінімізації коливань тренду та його згладжування.
А нестаціонарний процес з мінімальним трендом буде мати такі значення: р = 1, q = 1, Q(s) = 1
Основна модель ARIMA для загальних надходжень ПДФО матиме вигляд:
Переменная: VAR1
Преобразования: D(1)
Модель: (1,1,1)(0,0,1) Сезонный лаг: 12
Число набл.:53 Начальная SS=2510E6 Итоговая SS=1151E6 (45,84%) MS=2301E4
Параметры (p/Ps-авторегрессии, q/Qs-скольз. средн.); выделение: p<.05
p(1) q(1) Qs(1)
Оценка: -,1736 ,49883 -,5889
Ст.ошиб.: ,19216 ,14478 ,14202
Для визначення прогнозів необхідно зайти у прогнозні спостереження. В таблиці 6 наведено прогнозні рівні помісячних надходжень ПДФО з 90% довірчими межами.
Таблиця 6
