Завдання для індивідуальної та самостійної роботи
Розв’язати задачі за допомогою симплекс-методу:
3.01.
3.02.
3.03.
3.04.
3.05.
3.06.
3.07.
3.08.
3.09.
3.10.
3.11.
3.12.
3.13
3.14
3.15
3.16
3.17.
3.18.
=
3x1
-4x2-24x3-20x4-6x5
3.19. 3.20.
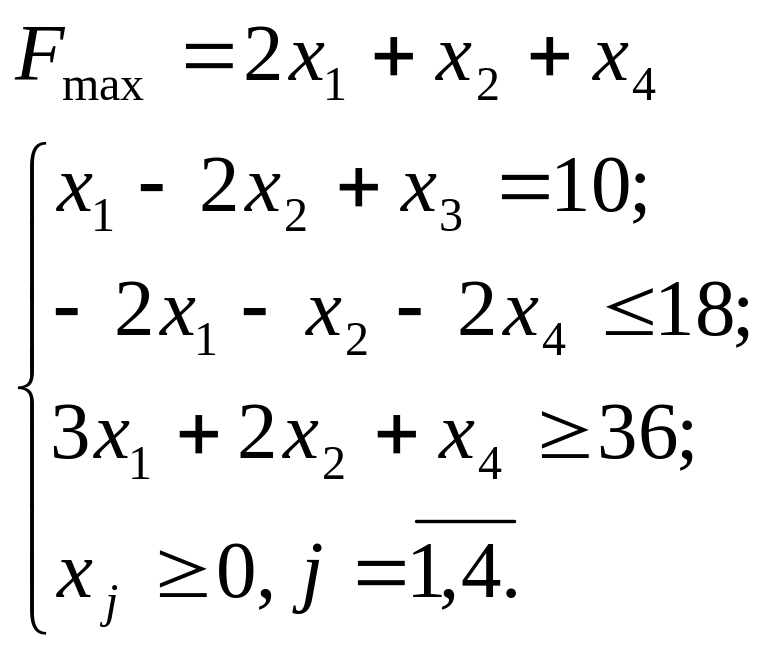
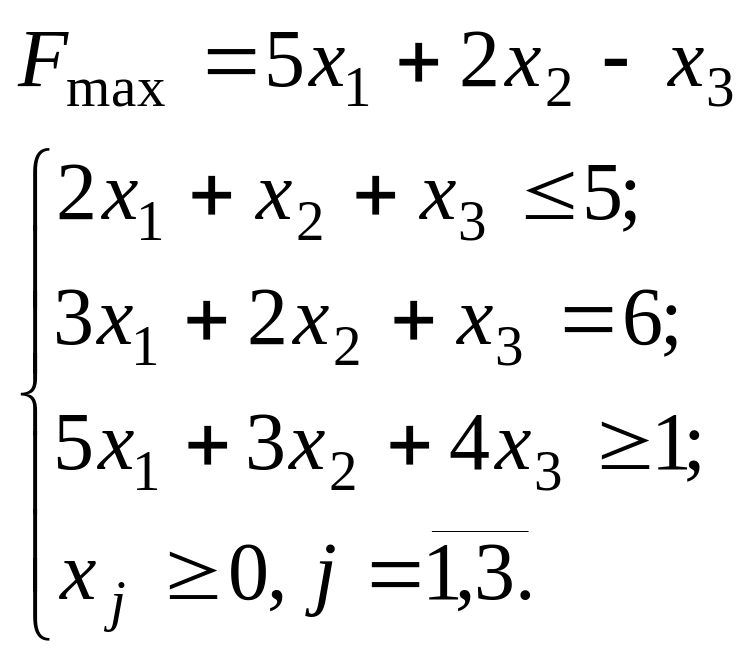
4. ТЕОРІЯ ДВОЇСТОСТІ У ЛІНІЙНОМУ
ПРОГРАМУВАННІ
4.1 ПОНЯТТЯ ДВОЇСТОСТІ.
ПРАВИЛА ПОБУДОВИ ДВОЇСТИХ ЗАДАЧ
Теорія двоїстості в лінійному програмуванні вивчає загальні властивості пари тісно пов’язаних між собою так званих двоїстих задач лінійного програмування. Виявляється, що з кожною задачею лінійного програмування пов’язана деяка інша, також цілком визначена задача лінійного програмування. Їх зв’язок взаємний і настільки тісний, що при розв’язуванні однієї з них фактично розв’язується й інша. Таку пару задач називають парою взаємно двоїстих задач лінійного програмування.
Правила побудови двоїстої задачі:
кожному обмеженню прямої задачі відповідає змінна двоїстої задачі. Кількість невідомих двоїстої задачі дорівнює кількості обмежень прямої задачі;
кожній змінній прямої задачі відповідає обмеження двоїстої задачі, причому кількість обмежень дорівнює кількості невідомих прямої задачі;
якщо цільова функція прямої задачі максимізації, то цільова функція двоїстої – мінімізації, і навпаки;
коефіцієнтами при змінних в цільовій функції двоїстої задачі є вільні члени системи обмежень прямої задачі;
вільні члени системи обмежень двоїстої задачі є коефіцієнти при змінних функції цілі прямої задачі;
матриця, що складається з коефіцієнтів при змінних у системі обмежень прямої задачі, і матриця коефіцієнтів в системі обмежень двоїстої задачі утворюються одна з одної транспонуванням, тобто заміною рядків стовпчиками, а стовпчиків – рядками.
Двоїсті пари задач лінійного програмування бувають симетричні та несиметричні. У симетричних задачах обмеження прямої та двоїстої задач є нерівностями, а змінні обох задач можуть набувати лише невід’ємних значень. У несиметричних задачах обмеження прямої задачі можуть бути записані як рівняння, а двоїстої - лише як нерівності. У цьому разі відповідні змінні двоїстої задачі набувають будь-якого значення, не обмеженого знаком.