- •1. Загальна задача лінійного програмування
- •1.1. Класифікація задач математичного програмування
- •1.2. Приклади задач лінійного програмування
- •Завдання для індивідуальної та самостійної роботи
- •2. Графічний метод
- •Завдання для індивідуальної та самостійної роботи Розв‘язати задачу лінійного програмування графічним методом (max, min):
- •3. Симплекс-метод розв’язування задачі лінійного програмування
- •3.1 Метод штучного базису
- •Завдання для індивідуальної та самостійної роботи
- •Пряма задача Двоїста задача
- •Симетричні
- •Несиметричні
- •4.2 Теореми двоїстості
- •Завдання для індивідуальної та самостійної роботи
- •5. Транспортна задача
- •5.1 Постановка транспортної задачі і побудова її математичної моделі
- •5.2. Методи пошуку опорних планів транспортної задачі
- •Метод північно-західного кута
- •Метод мінімальної вартості
- •5.3. Критерій оптимальності опорних розв’язків за методом потенціалів
- •5.4. Визначення оптимального плану тз, яка має ускладнення у постановці умови
- •Завдання для індивідуальної та самостійної роботи
- •6.2. Геометрична інтерпретація задачі параметричного програмування
- •6.3. Симплексний метод розв’язання задачі параметричного програмування
- •Завдання для індивідуальної та самостійної роботи
- •7. Задачa цілочисельного програмування
- •7.1. Геометрична інтерпретація задачі цілочисельного програмування
- •Розв’язування
- •7.2. Метод гоморі розв’язування задачі цілочисельного програмування
- •Етапи розв’язку задачі цілочисельного програмування методом гоморі :
- •Завдання для індивідуальної та самостійної роботи Знайти оптимальний цілочисельний розв’язок:
- •Література
Завдання для індивідуальної та самостійної роботи
5.01![]() 5.02.
5.02.
![]()
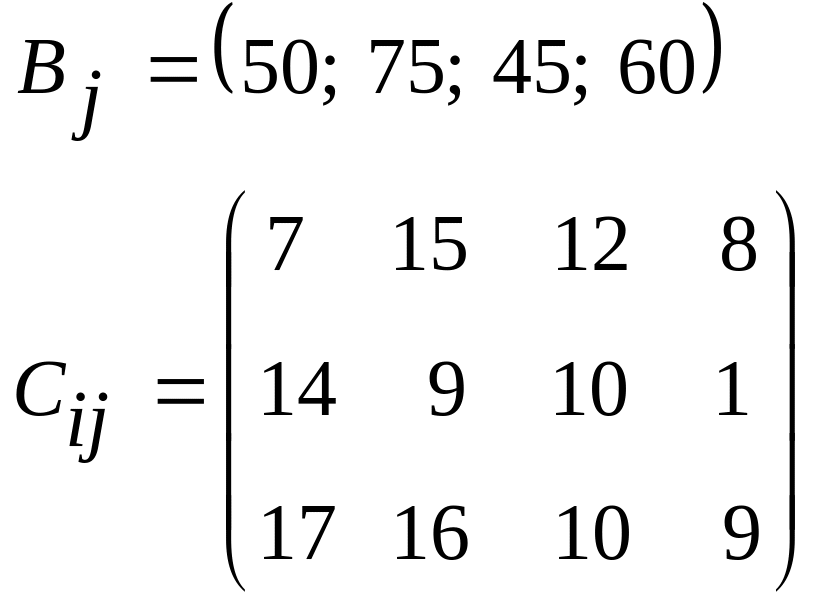
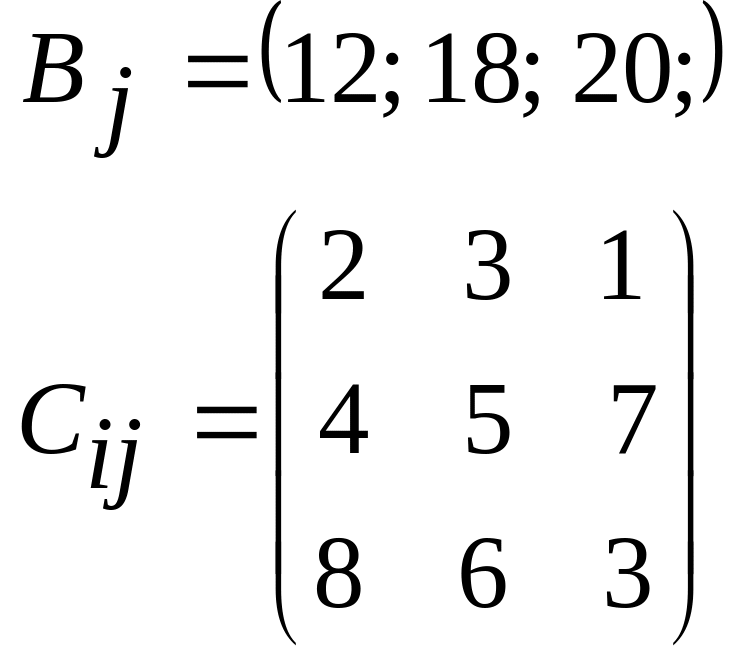
5.03.
![]() 5.04.
5.04.
![]()
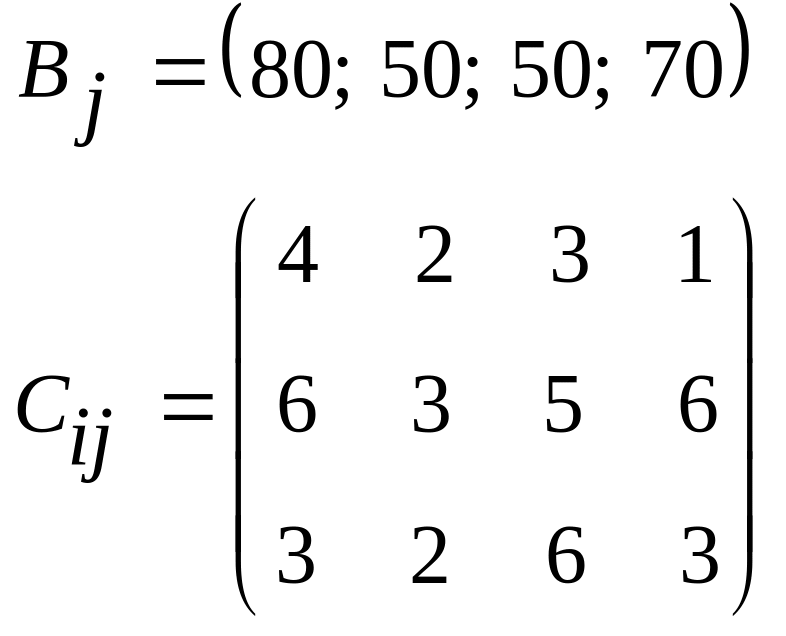
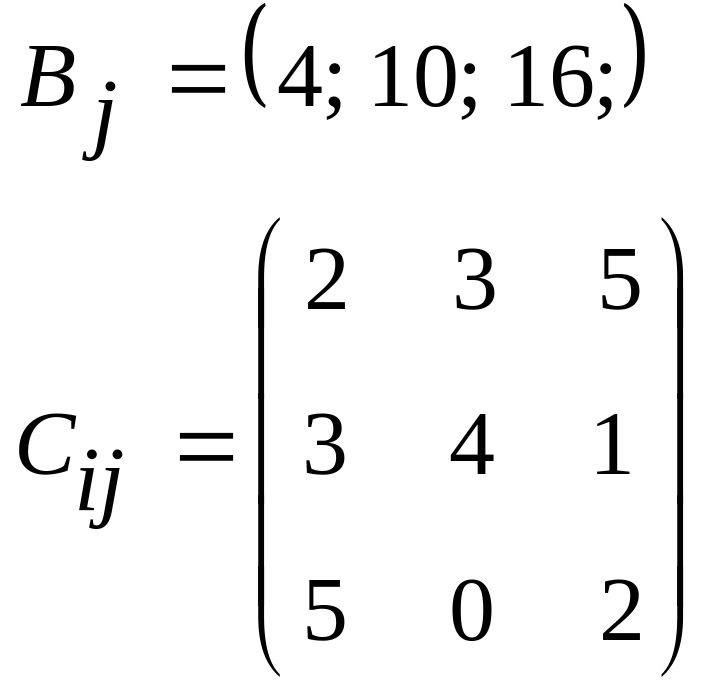
5.05.
![]() 5.06.
5.06.
![]()
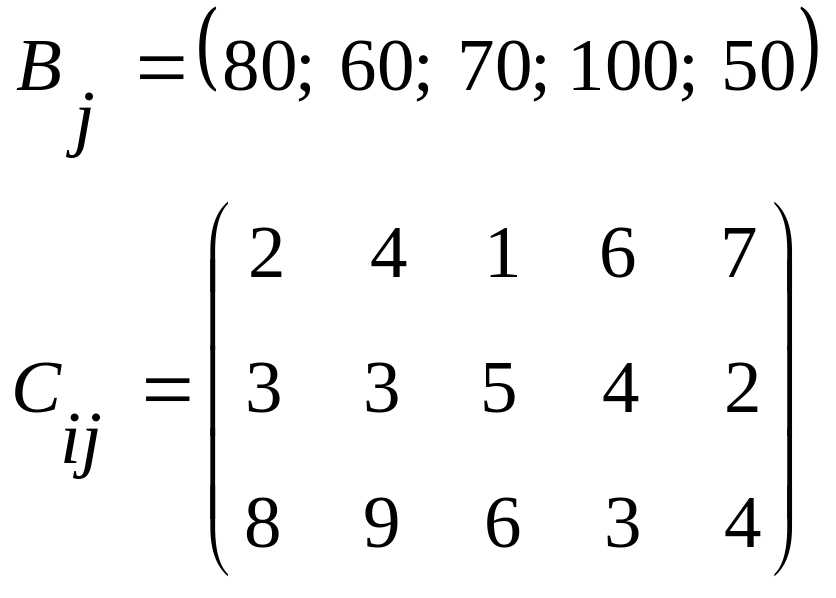
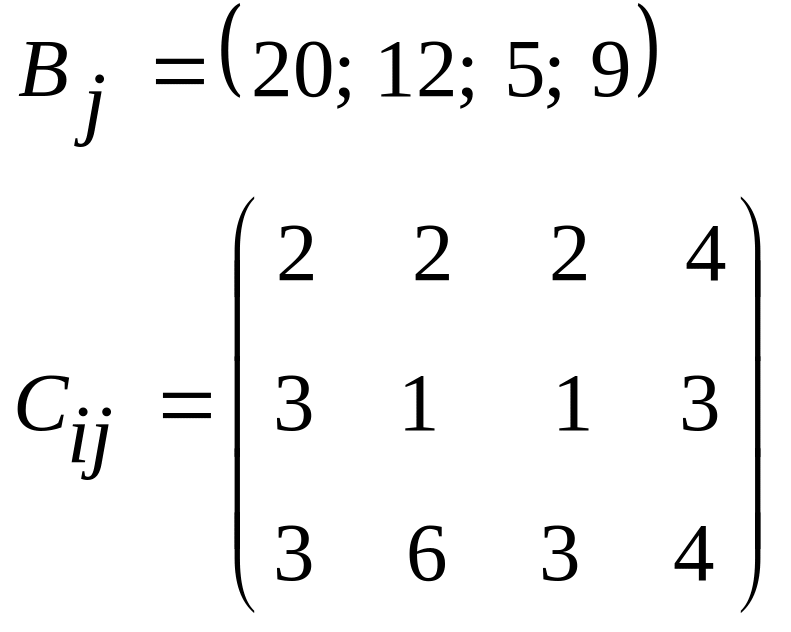
5.07.![]() 5.08.
5.08.
![]()
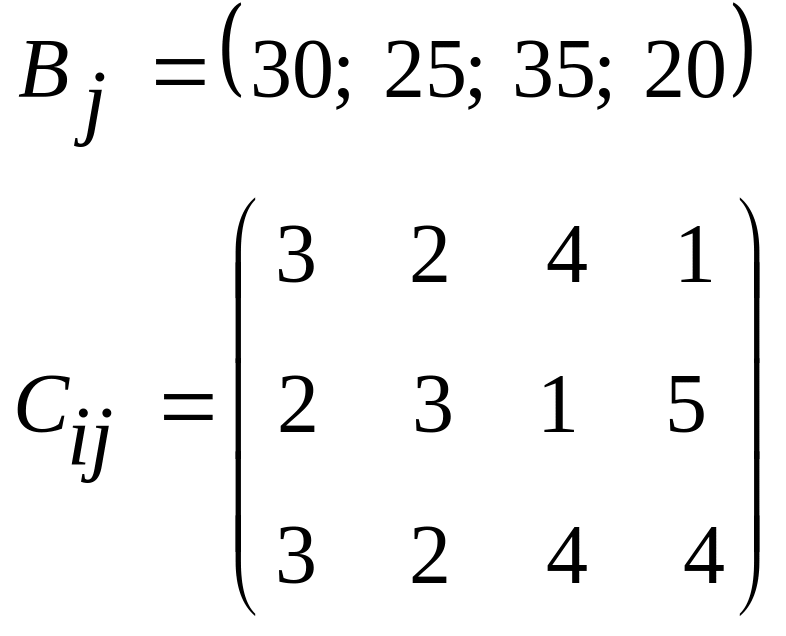
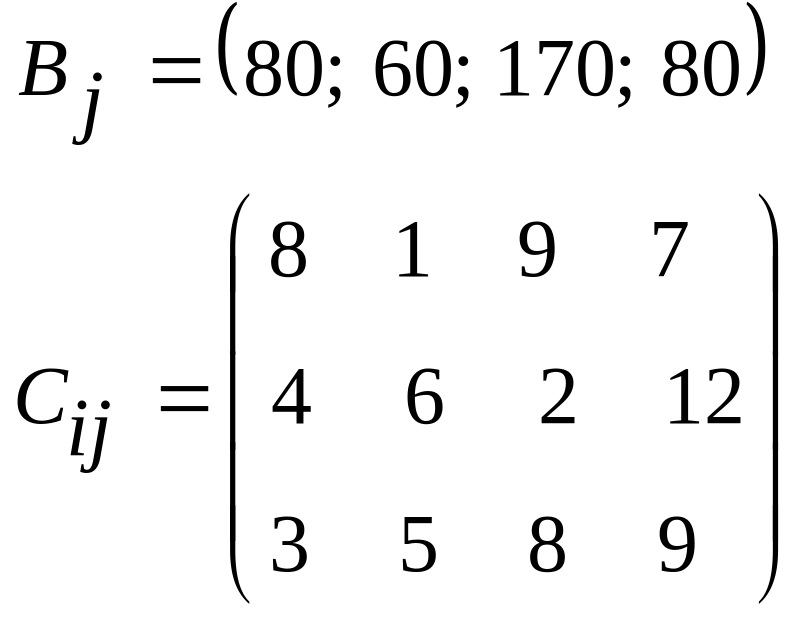
5.09.![]() 5.10.
5.10.
![]()
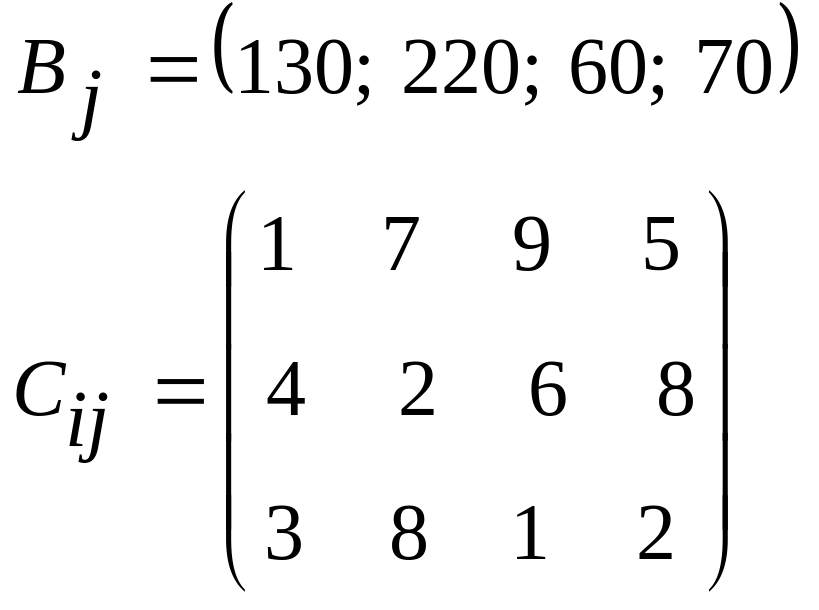
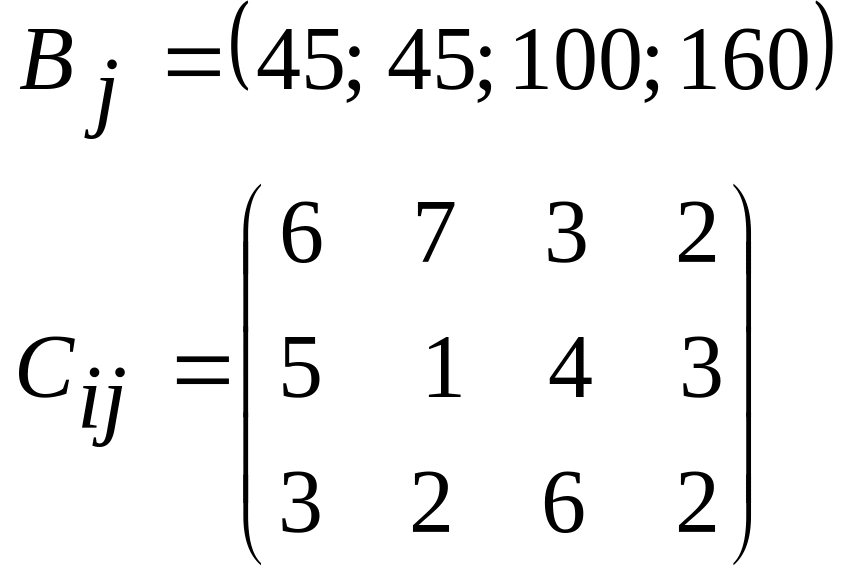
Аi=(140; 360; 180), Вj= (90; 120; 230;180; 60)

7 2 8 2 3
Сij = 4 3 1 5 6
5 2 3 2 8
з А1 до В2 та з А1 до В5 не можна перевозити
а з А2 до В3 треба перевезти 100 од. вантажу.
5 .12
. Аi=(160;180;170;200;190)
, Вj=(220;400;280)
.12
. Аi=(160;180;170;200;190)
, Вj=(220;400;280)
20 6 3
17 10 7
Сij= 13 9 13
2 4 6
17 15 12
з А2 до В2 перевезти 100 од. вантажу, а з А5 до В1 не можна перевозити.
Аi=(100;150;50), Вj=(75;80;60;85)

6 7 3 5
С ij= 1 2 5 6
8 10 20 1
з А2 до В2 перевезти не менше 60 од. вантажу, а з А1 до В4 - не більше 35 од.
5.14. Аi=(110;190;90), Вj=(80;60;170;80)
 8
1 9 7
8
1 9 7
Сij = 4 6 2 12
3 5 8 9
з А1 до В2 перевезти не менше 30 од. вантажу, а з А2 до В4 не більше 20 од.
Аi=(190;150;240;200;220), Вj=(300;330;370)

12 8 19
5 10 10
Сij = 16 21 4
8 15 16
11 10 12
з А2 до В2 перевезти не менше 100 од. вантажу, а з А3 до В1 не можна перевозити.
5 .16.
Аi=(120;110;130),
Вj=(80;60;70;100;60)
.16.
Аi=(120;110;130),
Вj=(80;60;70;100;60)
2 4 1 6 7
Сij= 1 2 3 5 2
8 9 6 4 3
з А2 до В2 та з А2 до В4 не можна перевозити.
Аi=(180;220;100), Вj=(120;80;160;90;50),
 1 2
3 1 4
1 2
3 1 4
Сij = 6 3 4 5 2
8 2 1 9 3
з А1 до В2 не можна перевозити, а з А2 до В1 перевезти 60 од. вантажу.
Аi=(150;170;190;210;180), Вj=(250;350;300)

7 13 14
9 16 15
Сij= 16 18 10
10 12 13
16 20 13
з А2 до В2 перевезти не більше 100 од. вантажу, а з А5 до В1 - 80 од. вантажу.
5.19. Аi= (170;190;140;180;120), Вj=(160;400;240),

6 10 11
13 14 4
Сij= 14 7 10
18 5 18
14 12 9
з А2 до В1 перевезти не менше 50 од. вантажу, а з А1 до В3 - 10 од.
5.20. Аi=(20;40;50), Вj=(30;25;35;20),

3 2 4 1
Сij= 2 3 1 5
3 2 4 4
з А1 до В2 перевезти 10 од. вантажу, а з А3 до В1 перевозити не можна.
6. ЗАДАЧА ПАРАМЕТРИЧНОГО ПРОГРАМУВАННЯ
6.1. ПОСТАНОВКА ЗАДАЧІ
ПАРАМЕТРИЧНОГО ПРОГРАМУВАННЯ
І ПОБУДОВА ЇЇ МАТЕМАТИЧНОЇ МОДЕЛІ
Як відомо, загальна задача лінійного програмування вміщує постійні величини: коефіцієнти cj, aij та вільні члени bi (i= ; j= ). З одного боку при визначенні цих величин на практиці зустрічаються з тим, що у дійсності вони не є постійними, а їх значення змінюються у деяких інтервалах. З іншого боку, після знаходження оптимального плану деякої економічної задачі при фіксованих значеннях cj, aij, bi, необхідно знати у яких допустимих межах їх можна змінювати, щоб план залишився оптимальним.
Тому виникає необхідність дослідити поведінку оптимального плану при зміні її коефіцієнтів та вільних членів. Дослідження подібного роду і складає предмет параметричного програмування.
Можна виділити слідуючи типи задач параметричного програмування:
Задача, у якій коефіцієнти цільової функції лінійно залежать від параметра t, полягає у знаходженні для кожного значення параметра t з проміжку його зміни , максимального значення функції

за
умовами
![]() ,
де cj,aij,bi
задані
постійні числа.
,
де cj,aij,bi
задані
постійні числа.
Якщо від параметра t лінійно залежать вільні члени системи обмежень, задача полягає у знаходженні для кожного значення параметра t з проміжку його зміни , максимального значення функції
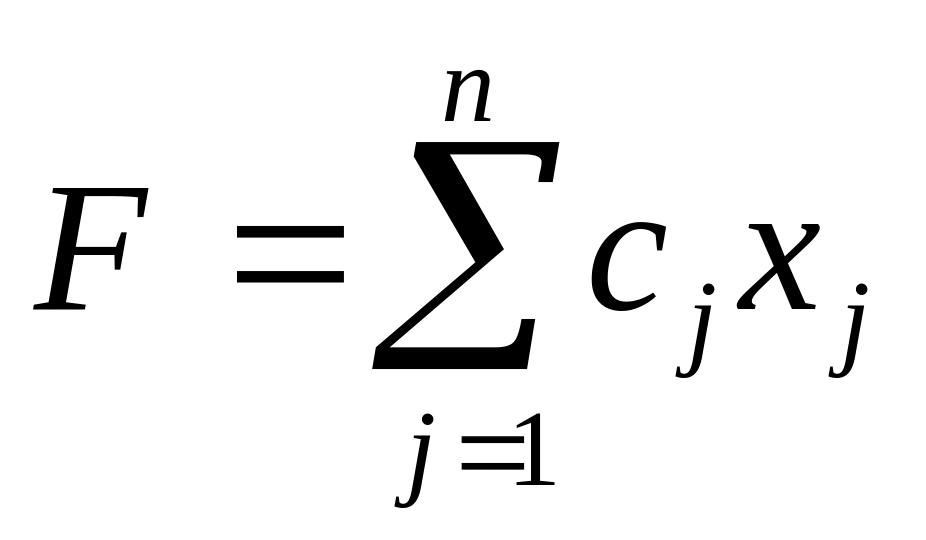 за
умовами
за
умовами
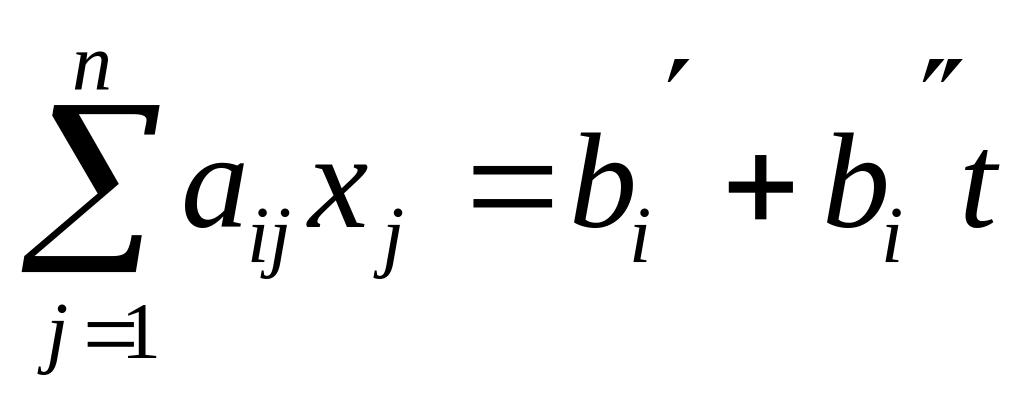 ,
де cj,aij,bi
задані постійні числа
,
де cj,aij,bi
задані постійні числаУ випадку, коли від параметра t лінійно залежать як коефіцієнти цільової функції, так й вільні члени системи обмежень; задача полягає у знаходженні для кожного значення параметра t з проміжку його зміни , максимального значення функції
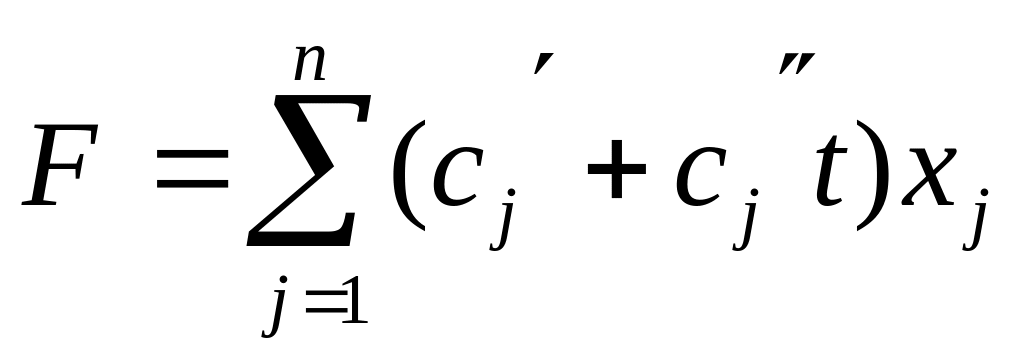 за умовами
за умовами
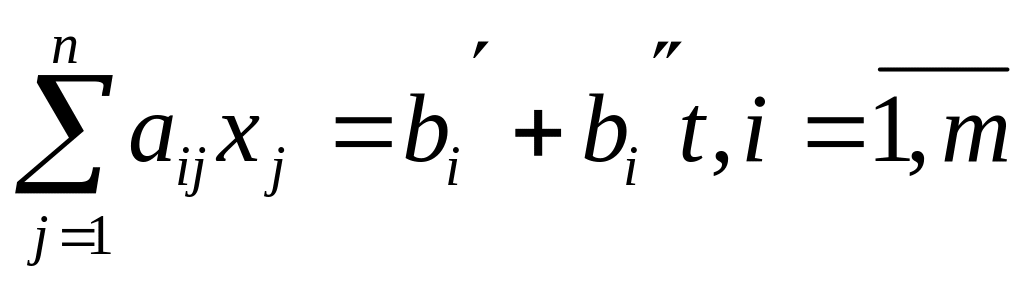 .
.Узагальненням цих задач є загальна задача параметричного програмування, у якій від параметра t лінійно залежать коефіцієнти при змінних цільової функції, коефіцієнти при змінних системи обмежень та вільні члени системи обмежень. Вона полягає у знаходженні для кожного значення t із , максимального значення функції
 за умовами
за умовами