4. Статистическое оценивание параметров цм , состоятельность оценок

Для статистического оценивания параметров ЦМ( ) будем пользоваться методом максимального правдоподобия.

Рассмотрим задачу построения оценок максимального правдоподобия (ОМП) для параметров 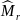шаблона 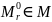и стохастической матрицы 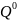по наблюдаемой реализации длительности .

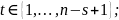
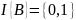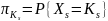Введем обозначения, пусть – мультииндекс -го порядка; – функция, которую назовем селектором -го порядка с параметрами и – индикатор события ; – начальное -мерное распределение вероятностей ЦМ ;

– частота -граммы для шаблона 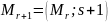, удовлетворяющая условию нормировки:

Для модели ЦМ логарифмическая функция правдоподобия имеет вид:

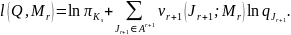
Для того, чтобы найти ОМП для матрицы , необходимо решить задачу на условный экстремум:

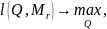
В результате получаем условную ОМП для матрицы ( ):

Далее рассматривается задачу поиска ОМП для шаблона .

Пусть – стационарное распределение вероятностей ЦМ . Пусть ЦМ – стационарна (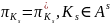 ), тогда распределение вероятностей 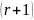-граммы для шаблона будет иметь следующий вид:

Соответствующая частотная оценка вероятностей:

.

Энтропия -мерного распределения вероятностей запишется в виде:

Количество информации по Шеннону, содержащейся в -грамме о будущем символе :

Логарифмическая функция правдоподобия для оценки имеет следующий вид:

где 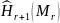– подстановочная оценка энтропии, получающаяся при подстановке вместо истинных значений 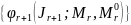их оценок { }.

Учитывая, что 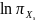не зависит от , добавляя также не зависящее от слагаемое 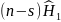, а также используя тот факт, что:

приходим к следующей ОМП шаблона :

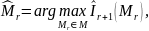
где 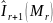– подстановочная оценка количества информации по Шеннону, получающаяся при подстановке вместо истинных значений их оценок { }.

Теорема 1. Если ЦМ является стационарной, то при истинном шаблоне и оценка состоятельна:

Теорема 2. Если ЦМ является стационарной и шаблон идентифицируемый, то при оценка состоятельна:

5. Статистическое оценивание параметров цм

Для ЦМ оценки параметров генератора с переменной обратной связью строятся аналогично модели с постоянной обратной связью с учетом периодически изменяющегося шаблона .

Логарифмическая функция правдоподобия имеет следующий вид:

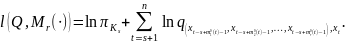
Задача на условный экстремум

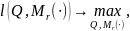
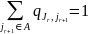
решается в общем виде, и это позволяет решить частную задачу оценки параметров генератора с переменной обратной связью.

Теорема 3. Если ЦМ является стационарной, то при истинном шаблоне и оценка состоятельна:

Теорема 4. Если ЦМ является стационарной и шаблон идентифицируемый, то при оценка состоятельна:

2. Практическая часть

   1. Описание программы

Построена компьютерная модель цепи Маркова с частичными связями и переменным шаблоном со следующими входными параметрами:

• глубина предыстории однородной цепи Маркова ЦМ .

• длина временного ряда с пространством состояний .

• Шаблоны 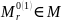и 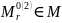, которые повторяются с периодом

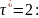
• Стохастическая матрица вероятностей одношаговых переходов для шаблонов:

В частном случае, при данная матрица имеет следующий вид:

Реализовано моделирование цепи Маркова с частичными связями и переменным шаблоном, нахождение оценок максимального правдоподобия матрицы вероятностей одношаговых переходов и переменного шаблона смоделированного временного ряда. Далее более подробно рассматривается алгоритм работы программы.