МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ ПРИКЛАДНОЙ МАТЕМАТИКИ И ИНФОРМАТИКИ

Кафедра математического моделирования и анализа данных

ЦЕПЬ МАРКОВА С ЧАСТИЧНЫМИ СВЯЗЯМИ И ПЕРЕМЕННЫМ ШАБЛОНОМ

Курсовая работа

Батуры Олега Владимировича

студента 3 курса,

специальность

«Компьютерная безопасность»

Научный руководитель:

доктор физ.-мат. наук,

заведующий кафедрой ММАД

Ю. С. Харин

Минск, 2015

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ ПРИКЛАДНОЙ математики и информатики

Кафедра математического моделирования и анализа данных

ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ

Студент Батура Олег Владимирович, 3 курс, 9 группа

1. Тема работы Цепь Маркова с частичными связями и переменным шаблоном

2.  Срок сдачи студентом законченной работы ________ 2015 г.

3. Перечень вопросов, подлежащих разработке

• Исследовать вероятностные характеристики модели цепи Маркова с частичными связями и переменным шаблоном. Найти -мерное распределение вероятностей .

• Построить компьютерную модель ЦМ с переменным шаблоном.

• Построить статистические оценки параметров модели при известной функции шаблона 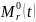, исследовать свойства оценок.

• Построить оценки параметров модели при периодически изменяющемся, но неизвестном шаблоне.

Руководитель курсовой работы______________ / Ю. С. Харин/ ______ 2015 г.

Задание принял к исполнению_______________ 2015 г.

ОГЛАВЛЕНИЕ

Введение 4

1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 5

1.1. Цепь Маркова порядка 5

1.2. Цепь Маркова с частичными связями ЦМ 6

1.3. Цепь Маркова с частичными связями и переменным шаблоном ЦМ 8

1.4. Статистическое оценивание параметров ЦМ, состоятельность оценок 10

1.5. Статистическое оценивание параметров ЦМ 14

2. ПРАКТИЧЕСКАЯ ЧАСТЬ 15

2.1. Описание программы 15

2.2. Моделирование временного ряда длительности 16

2.3. Построение оценок максимального правдоподобия и 17

2.4. Результаты экспериментов 20

2.5. Вывод 22

Заключение 23

Список использованной литературы 24

Введение

При математическом моделировании сложных систем и процессов в различных научных сферах часто возникает необходимость построения вероятностно-статистических моделей дискретных временных рядов 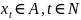, где пространство состояний 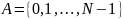— конечное множество мощности 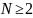с длинной памятью [1]. Известной моделью таких дискретных временных рядов является цепь Маркова достаточно высокого порядка , определяющего длину памяти; если 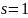, то цепь Маркова называется простой, если 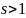— сложной. 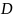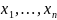Однако для такой модели число параметров растет экспоненциально при увеличении порядка : , и для статистического оценивания параметров требуется иметь реализацию не всегда доступной на практике длительности . В связи с этим актуальна проблема построения малопараметрических моделей цепей Маркова высокого порядка. В данной работе исследуется малопараметрическая модель цепи Маркова порядка с частичными связями ЦМ , рассмотренная в [2], для которой шаблон связей зависит от времени, исследуются ее вероятностные характеристики, строятся статистические оценки параметров при известной функции шаблона, а также при периодически изменяющемся, но неизвестном шаблоне.

1. Теоретическая часть

   1. Цепь Маркова порядка

В криптологии для моделирования дискретных временных рядов с глубиной памяти используется цепь Маркова порядка (ЦМ ), обобщающая модель простой цепи Маркова [3].

Определение. Цепь Маркова , порядка с пространством состояний , определенная на вероятностном пространстве ( ) и временной области , характеризуется обобщенным марковским свойством:

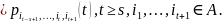
Это означает, что условное распределение вероятностей будущих состояний при фиксированной предыстории зависит не от всей этой предыстории, а от ближайшей на глубину предыстории

Цепь Маркова ЦМ( ) характеризуется -мерным начальным распределением вероятностей

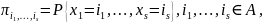
и -мерной матрицей вероятностей одношаговых переходов в момент времени :

=

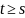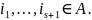
Матрица при этом удовлетворяет условиям нормировки (если она не зависит от времени, то есть , ЦМ( ) в таком случае называется однородной):

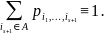
В таком случае -мерное распределение вероятностей имеет вид:

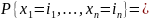
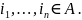
Число независимых параметров, определяющих матрицу вероятностей одношаговых переходов для однородной ЦМ( ), равно .

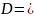
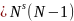При увеличении глубины памяти число параметров экспоненциально возрастает, и для идентификации такой модели требуется наблюдать реализацию не всегда доступной на практике длительности .

Возникает задача поиска малопараметрической модели цепи Маркова высокого порядка, для которой число параметров в матрице задается числом параметров . Одной из таких моделей является цепь Маркова порядка с частичными связями (ЦМ ) [2].