Решение задач. Задача 1

Задача 1.34.

Для подъема (рис. а) или опускания (рис. б) каменного блока А, весящего 2000 кг, применили два клина В и С. Коэффициент трения для соприкасающихся поверхностей АВ и АС равен f= 0,2, а для поверхностей BD и CD равен f₂=0,25.

Найти равные по величине горизонтальные силы Р, сжимающие клинья, необходимые для подъема блока А. Определить силы Р, растягивающие клинья, необходимые для опускания блока А. Наклонные плоскости соприкосновения блока с клиньями образуют угол 10⁰ с горизонтом.

Решение.

Рассмотрим равновесие системы тел, состоящей из блока А и клиньев В и С. При подъеме блока (рис. а) силы Р сжимают клинья. Рассмотрим отдельно равновесие блока и равновесие клина. Отбросив мысленно клинья, заменим их действие на блок нормальными реакциями N и силами трения F (рис. в) Кроме того, на блок действует известная сила – вес Q. Составим два уравнения равновесия, приравнивая нулю суммы проекций всех сил на оси x и y:

Кроме того, запишем зависимость сил трения от нормального давления

Тогда находим:

N₁=N₂=1050 кг, F₁=F₂=210 кг.

Перейдем, далее, к рассмотрению равновесия клина В (рис. г). На клин действуют: реакция блока, которая раскладывается на нормальную составляющую – N, и силу трения – F, активная сила Р и реакция пола, расположенная на нормальную силу S и силу трения Т. Напишем уравнения р авновесия для клина В:

Кроме того, имеем зависимость силы трения от нормального давления

Отсюда, пользуясь найденными ранее значениями реакций, найдем

S= 996 кг, T= 249 кг, Р=641 кг.

Таким образом, для равновесия системы при подъеме блока получено необходимое граничное значение силы Р = 641 кг. Если же Р > 641 кг, то начнется подъем блока; система придет в движение.

Перейдем к определению величины силы Р при спуске блока. Блок А находится в равновесии (рис. д) под действием активной силы – веса Q, нормальных реакций клиньев N₁ и N₂ и сил трения F₁ и F₂. Силы трения в этом случае направлены вдоль наклонной плоскости вверх. Это сразу видно из рассмотрения равновесия клина В (рис. е), так как в связи с изменением направления силы Р на прямо противоположные силы Т и -F₂ меняют свое направление на противоположное по сравнению с предыдущим случаем (рис. г).

Уравнения равновесия для блока А будут:

Кроме того, зависимость силы трения от нормального давления дается равенствами

Отсюда находим:

N₁=N₂=980 кг, F₁=F₂=196 кг.

Уравнения равновесия для клина В (рис. е) будут:

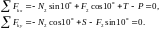
Сила трения выражается через нормальное давление

Отсюда, пользуясь ранее найденными значениями реакций N₂ и F₂, найдем:

S= 999 кг, T= 250 кг, Р=273 кг.

Найденное значение Р является граничным при равновесии системы в случае опускания блока.

Таким образом, на основании проведенного исследования можно заключить, что система будет находиться в равновесии, если проекция силы Р лежит в пределах

Если модуль каждой из сил Р будет больше 641 кг, то при их направлении, указанном на рис. а, начнется подъем блока. Для того, чтобы блок начал опускаться, нужно приложить силы Р в противоположном направлении, причем их модуль должен превышать 273 кг.