
§ 2. Определение сил по заданному движению
(прямая задача динамики материальной точки)
Если даны уравнения
движения материальной точки массы m
в декартовых координатах:
 то
проекции
то
проекции
 силы
силы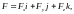 вызывающие
это движение, определяются по формулам:
вызывающие
это движение, определяются по формулам:
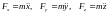 (1*)
(1*)
Откуда

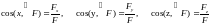
Таким образом, прямая задача динамики материальной точки легко решается посредством дифференцирования заданных уравнений движения точки.
Если дано уравнение
движения материальной точки массы m
по траектории, т. е.,
 то проекции
то проекции
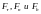 силы
силы вызывающей это движение, определяются
по формулам:
вызывающей это движение, определяются
по формулам:
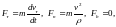 (2*)
(2*)
Откуда
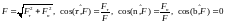
В формулах (2*)
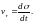
Если даны уравнения
плоского движения материальной точки
массы m в полярных
координатах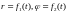 ,
то проекции
,
то проекции
 силы
F, вызывающей это движение, определяются
по формулам:
силы
F, вызывающей это движение, определяются
по формулам:
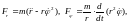 (3*)
(3*)
Откуда
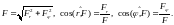
Сила, приложенная к материальной точке, называется центральной, если линия ее действия проходит во время движения через неподвижную точку, называемую центром. Сила, непременная к неподвижному центру, называется силой притяжения. Сила, направленная от неподвижного центра, называется силой отталкивания. Движение материальной точки под действием центральной силы происходит в плоскости, проходящей через вектор-радиус и начальную скорость точки. Для его исследования удобно ввести полярные координаты и использовать формулу Бине

где С—секториальная
скорость точки, которая при наличии
центральной силы постоянна:
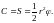 (Секториальной скоростью S называется
производная по времени от площади S,
описываемой вектор-радиусом г движущейся
точки.)
(Секториальной скоростью S называется
производная по времени от площади S,
описываемой вектор-радиусом г движущейся
точки.)
Применение формулы
Бине позволяет определить закон изменения
центральной силы по данном) уравнению
нейтральном орбиты (прямая задача). Если
 оказывается
положительной, то центральная сила
является силой отталкивания, если —
отрицательной, то — силой притяжения.
оказывается
положительной, то центральная сила
является силой отталкивания, если —
отрицательной, то — силой притяжения.
Прямые задачи динамики несвободной материальной точки, в которых требуется определить задаваемую силу или силу реакции, приложенную к точке, рекомендуется решать в следующем порядке:
1) изобразить на рисунке материальную точку в текущем положении и приложенные к пей задаваемые силы;
2) применив принцип освобождаемости от связей, изобразить соответствующие силы реакций связей;
3) выбрать систему отсчета, если она не указана в условии задачи;
4) определить по заданному закону движения ускорение материальной точки и найти его проекции на выбранные оси координат;
5) составить дифференциальные уравнения движения материальной точки, соответствующие принятой системе отсчета;
6) из системы составленных уравнений определить искомую величину.
