Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Башкирский государственный университет»

Отчет по учебной практике

Власюка Андрея Леонидовича, группа 24

^{(Ф.И.О. студента, группа)}

Направление подготовки _______010302 Прикладная математика и информатика

Профиль_______________________________________________________________________

Факультет_____________математики и информационных технологий___________

Кафедра________ Механика сплошных сред___________________________________

Сроки практики _______________17.08.2015-29.08.2015_______________________________

Теоретический материал. Алгоритмы решения.

Равновесие тел при наличии трения

1°. Равновесие твердого тела при наличии трения скольжения. Силы трения скольжения возникают между шероховатым телом и шероховатой поверхностью, если равнодействующая активных сил R не направлена по нормали к поверхности, на которой покоится тело (рис. 1.36). При равновесии тела необходимо, чтобы реакция шероховатой поверхности 5 (рис. 1.37) равнялась по величине Л и была направлена в прямо противоположную сторону. Разложим активную силу R на нормальную составляющую N и касательную составляющую Т, реакцию шероховатой поверхности на нормальную составляющую Nt и касательную составляющую F, называемую силой трения скольжения или силой трения первого рода.

При равновесии должны соблюдаться равенства

N—Ni = 0, (1*)

T — F = Q. (2*)

Из опыта известно, что при изменении величины составляющей Т в определенных пределах равновесие тела не нарушается. Следовательно, и сила трения скольжения согласно уравнению (2*) будет меняться в этих пределах. Таким образом, сила трения скольжения при покое есть составляющая реакции связи, возникающая при действии активных сил, стремящихся сдвинуть тело. Эта составляющая реакции направлена в сторону, противоположную возможному движению тела. Величина силы трения может меняться от нуля до некоторого предела, в зависимости от величины и направления активных сил, с тем чтобы

воспрепятствовать перемещению тела. Отличие силы трения от других реакций связей заключается и том, что ее модуль не может превысить определенного предела. Зависимость между силой трения и нормальным давлением определяется законом Кулона: наибольшая величина силы трения скольжения пропорциональна нормальному давлению тела на поверхность

(3*)

Сила трения всегда направлена в сторону, противоположную возможному относительному движению. Постоянная называется коэффициентом трения скольжения. Экспериментально установлено, что этот коэффициент зависит от материала соприкасающихся тел и их шероховатости (чистоты обработки). Для абсолютно гладких тел коэффициент ранен пулю. Для реальных тел

(4*)

Коэффициент трения не зависит от силы нормального давления и площади соприкосновения.

Угол 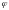между нормалью к поверхности и полной ее реакцией в положении предельного равновесия, когда , называется углом трения (рис. 1.38). Этот угол определяется равенством

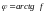т.е. (5*)

Построим в точке соприкосновения нормаль к поверхности и прямую ОА, составляющую с ней угол . Конус, описанный этой прямой как образующей, называется конусом трения. Если линия действия равнодействующей активных сил, приложенных к твердому телу, лежит внутри конуса трения, то вне, зависимости от ее модуля тело останется в покое. Это объясняется тем, что в этом случае движущая сила будет меньше предельной силы трения.

Действительно, рассмотрим равновесие тела, находящегося на горизонтальной плоскости S (рис. 1.39). К телу приложена равнодействующая активных сил Q под углом к нормали (вес тела входит в Q). Коэффициент трения скольжения известен. Полагая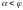 , составим уравнение равновесия, приравняв пулю сумму проекций всех сил на направление нормали (рис. 1,40):

или (6*)

Проектируя все силы на горизонтальное направление, находим:

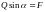или (7*)

Замечая, что наибольшее зн;1чение силы трения равно

(8*)

и учитывая, что ,заключаем:

(9*)

Следовательно, сила Q, линия действия которой находится внутри конуса трения, не может сдвинуть тело с места, как бы велика она ни была. На этом свойстве основаны некоторые самотормозящиеся устройства. Если из Q выделить вес тела Р, то неравенство (9*) примет вид

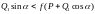(10*)

Следовательно, сила Q, не может нарушить равновесие тела при

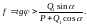(11*)

н аибольшей величины. Поэтому уравнения равновесия твердого тела, которые выражались равенствами (§ 2, уравнения (1*), (2*), (3*),при наличии сил трения превращаются в неравенства. В связи с этим при решении задач, как правило, рассматривают наибольшее значение силы трения и находят при этом из уравнений равновесия предельные (наибольшие и наименьшие) значения искомых величин. Так, например, рассматривая равновесие лестницы АВ (рис. 1.41), опирающейся на гладкую стену и шероховатый пол, мы найдем наименьшее значение угла , при котором лестница будет в покое, если возьмем максимальное значение силы трения. Положений равновесия лестницы будет при этом бесчисленное множество, так как при любом значении угла , большем найденного, но меньшем 90°, для равновесия необходима сила трения меньшая, чем ее максимальная величина.

При решении задач на равновесие твердого тела при наличии сил трения Рис. 1.41. следует выполнить четыре первых пункта, указанных в начале книг на стр. 15. При этом следует реакцию шероховатой поверхности представить двумя составляющими — нормальной реакцией и силой трения, или же, не раскладывая эту реакцию па составляющие, направить ее под углом трения к нормали к поверхности (при максимальной силе трепля);

5) сопоставить число неизвестных величии п число независимых уравнений равновесия, которые должны быть равны для статически определенных задач; при этом к уравнениям равновесия твердого тела следует добавить зависимость силы трения от нормального давления (3*);

6) выбрать систему координат;

7) составить систему уравнений равновесия для сил, приложенных к твердому телу или к системе твердых тел;

8) решив систему уравнений равновесия, определить искомые величины.