1.3. Теоретические распределения наработки до отказа

Возможны два пути вычисления показателей надежности неремонтируемых объектов по данным об отказах:

1) вычисление экспериментального распределения наработки до отказа;

2) вычисление параметров теоретического распределения наработки до отказа.

Оба пути имеют достоинства и недостатки. Исторически сложилось так, что вероятностные методы исследования в основном развиваются по пути использования теоретических распределений.

В качестве теоретических распределений наработки до отказа могут быть использованы любые применяемые в теории вероятностей непрерывные распределения. В принципе можно взять любую кривую, площадь под которой равна единице, и использовать ее в качестве кривой распределения случайной величины.

На рис. 4 приведены графики f(t) и λ(t) для четырех наиболее часто употребляемых в теории вероятностей распределений, а соответствующие функции надежности – на рис. 5.

Рис. 4. Графики λ(t) и f(t) теоретических законов распределения наработки до отказа: а – нормальное, [усеченное на интервале (0, ∞)]; б – равномерной плотности; в – показательное; г – Релея

Рис. 5. Графики функций надежности. Распределения: 1 – нормальное [усеченное на интервале (0, ∞)]; 2 – равномерной плотности; 3 – показательное; 4 – Релея

1.3.1. Показательное (экспоненциальное) распределение

При показательном распределении наработки до отказа

λ =const; m_t = 1/λ.

Дисперсия наработки до отказа

Показательное распределение применяется чаще других при исследовании надежности изделий. Это объясняется рядом причин.

Во-первых, показательное распределение наработки до отказа типично для сложных объектов, состоящих из многих элементов с различными распределениями наработки до отказа.

Во-вторых, при постоянных интенсивностях отказов изделий получаются очень простые формулы для расчета надежности. Это связано с тем, что при λ =const вероятность безотказной работы в течение заданной наработки Δt не зависит от суммарной наработки.

В-третьих, при ограниченных экспериментальных данных трудно обнаружить значительные отклонения от гипотезы λ =const, даже если и имеется возможная нестационарность λ(t). Если экспериментальных данных недостаточно, чтобы выявить истинный характер нестационарности λ(t), принимают в качестве первого приближения λ = const.

1.3.2. Усеченное нормальное распределение

При нормальном (гауссовом) распределении случайной величины она может принимать любые значения от –∞ до +∞. Поскольку возможные значения случайной наработки до отказа Т могут быть только положительными, распределение Т может быть лишь усеченным нормальным.

Усеченным нормальным распределением случайной величины называется распределение, получаемое из нормального при ограничении интервала возможных значений этой величины. Так как возможные значения случайной величины Т ограничены интервалом (t₁, t₂), то плотность усеченного распределения

где

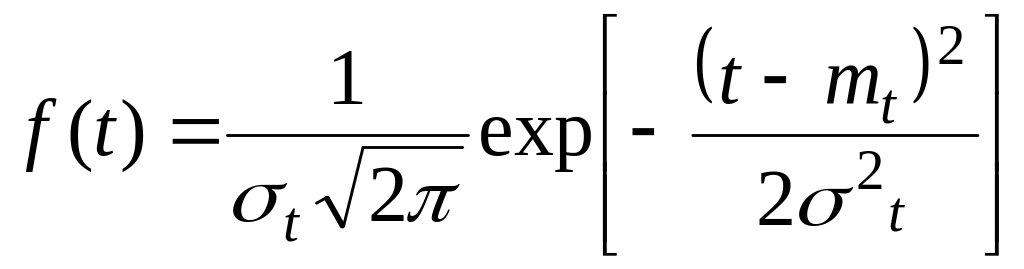(15)

f(t) – плотность неусеченного распределения; с – нормирующий множитель, находимый из условия, что площадь под кривой распределения равна единице, т. е.

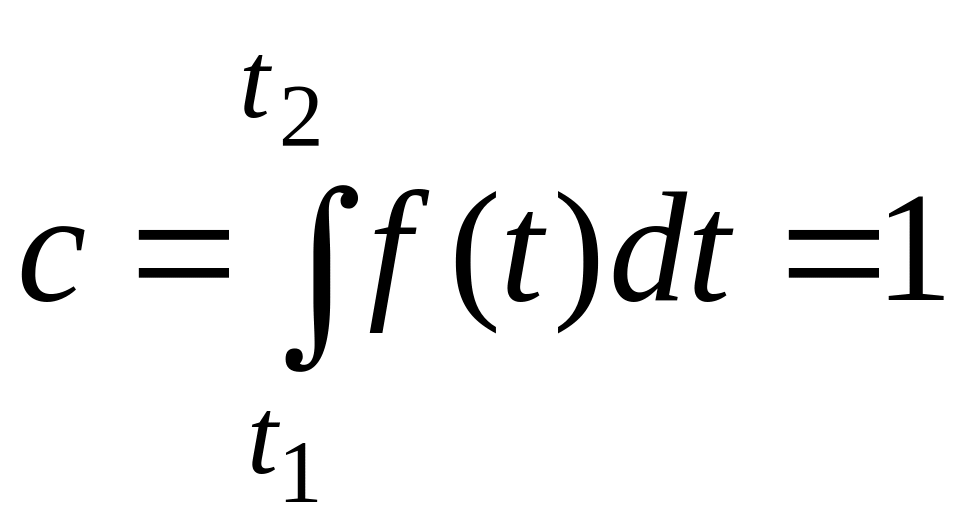
или

(16)

Подставив в (16) выражение для f(t) и применив подстановку

где m_t, σ_t – среднее значение и среднее квадратическое отклонение неусеченного распределения, после преобразования получим:

(17)

где

– нормированная функция Лапласа.

Функция надежности

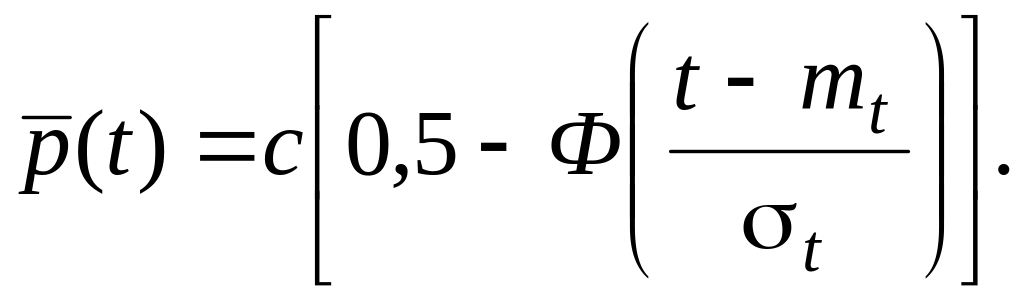(18)

Интенсивность отказов

Найдем формулы для числовых характеристик усеченного нормального распределения: математического ожидания наработки до отказа и дисперсии наработки до отказа . Согласно определениям этих характеристик имеем

(19)

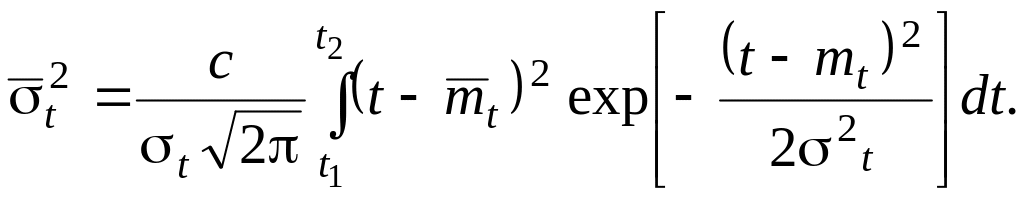(20)

Проведя преобразования, получим:

(21)

(22)

где

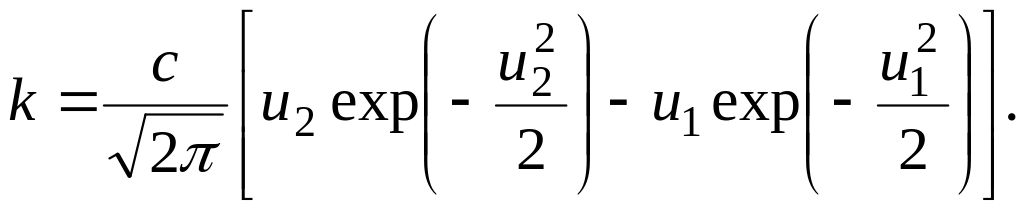(23)

Когда возможные значения случайной величины Т лежат в интервале (0, ∞), из формул (17), (19) – (23) получаем:

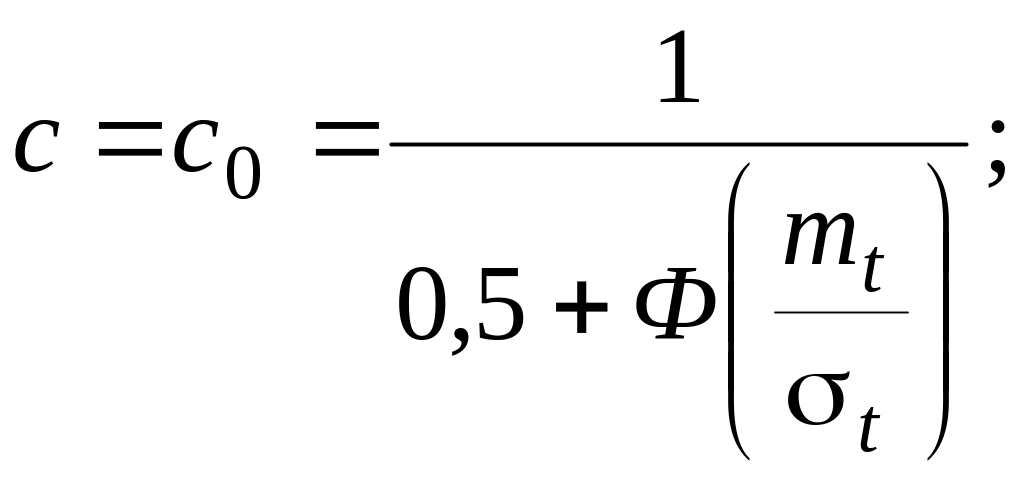(24)

(25)

(26)

(27)

На рис. 6 приведены зависимости отношений числовых характеристик усеченного и неусеченного нормального распределений и значения нормирующего множителя c₀ от отношения m_t /σ_t.

Рис. 6. Зависимость отношений числовых характеристик усеченного и неусеченного нормального распределения и нормирующего множителя c₀ от отношения m_t/σ_t. (Черта над , означает, что эти характеристики относятся к усеченному распределению)

Из рис. 6 следует, что при m_t /σ_t >2, что обычно и имеет место на практике при употреблении нормального распределения, значение c₀ очень мало отличается от единицы и , . Поэтому в дальнейшем не будем добавлять термин «усеченное» к названию «нормальное распределение наработки до отказа».

Необходимо отметить, что вопреки распространенному мнению при отказах элементов за счет износа распределение наработки до отказа будет далеко не всегда нормальным. Необходимым условием нормального распределения наработки до отказа является малый разброс значений скорости износа элементов.

Ввиду большого теоретического и прикладного значения нормального распределения его стараются иногда применить и при явно несимметричных распределениях наработки до отказа. Для этого подбирают некоторую функцию случайной наработки до отказа, например lgT, T² и т. д., приближенно следующую нормальному закону. Например, довольно часто используется логарифмически нормальное распределение усталостной долговечности, при котором предполагается, что логарифм числа циклов нагрузки до разрушения образца распределен по нормальному закону.