Практическая работа №6

Изучение распределения молекул идеального газа по скоростям

1. Подготовительная часть.

1. Для данной работы необходимо повторить физические величины, постоянные и законы, изучаемые в МКТ. Для этого необходимо заполнить следующую таблицу.

   Название величины	Обозначение величины	Единица измерения	Значение	Связь с другими величинами
   Масса молекулы
   Количество молекул
   Молярная масса
   Количество вещества
   Концентрация молекул в веществе
   Скорость движения молекулы
   Кинетическая энергия движения молекулы
   Постоянная Авогадро
   Постоянная Больцмана
   Основное уравнение МКТ

2. Прочитайте текст и заполните пустые места, ответьте на вопросы, а также произведите необходимые расчёты.

Любое вещество в земных условиях состоит из огромного числа молекул. Сколько частиц содержит 1 моль вещества? .

Математическое описание такой системы возможно лишь при рациональном выборе ее физической модели. Использование какой физической модели означает, что свойства различных разреженных газов не должны существенно отличаться друг от друга? Опишите эту модель.

1) ,

2) ,

3) .

За одни сутки молекулы воздуха ударяют каждого из нас примерно раз. Их средняя скорость в 1,5 раза превышает скорость звука. Из-за столкновения друг с другом молекулы изменяют направление своего движения. Если предположить, что сначала все молекулы двигались горизонтально, то уже после первого столкновения часть молекул в результате нецентрального удара изменит направление движения (рис 1).

Рис 1 Рис 2

С каждым последующим столкновением возрастает хаотичность движения молекул. В результате частых столкновений любая молекула может двигаться в произвольно выбранном направлении с такой же вероятностью, как и в любом другом. В результате столкновений друг с другом молекулы идеального газа изменяют не только направление своего движения, но и значение скорости.

Для определения положения и скорости всех частиц идеального газа в произвольный момент времени можно воспользоваться законами динамики Ньютона для каждой частицы. Для описания движения всех частиц лишь в 1 моле газа потребуется решить таких уравнений. Кроме того, получение информации об отдельной частице не представляет практического интереса для описания поведения газа как целого. Информация о системе с большим числом частиц должна содержать сведения не об отдельной частице, а обо всей совокупности частиц в целом. Подобный обобщенный подход называется .

МКТ выявляет взаимосвязь и параметров.

Ее цель – объяснить свойства вещества, зная характерные особенности его

.

Ответить на вопрос, сколько частиц обладает определенной скоростью, невозможно. Для определения статистического распределения молекул идеального газа по скоростям выбирается определенный интервал значения скорости.

Среднее значение физической величины можно рассчитать по следующей формуле:

(1)

В данном вопросе формула примет вид:

(1’)

где 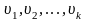- возможные значения скоростей молекул идеального газа,

- количество молекул, составляющих соответствующую скоростную группу,

N – количество скоростных групп.

Первое экспериментальное определение скоростей молекул выполнено немецким физиком О.Штерном (1888-1970) в 1920 г. его опыт позволил оценить распределение молекул по скоростям. Схема установки Штерна представлена на рис. 2. Вдоль оси внутреннего цилиндра с щелью натянута платиновая проволока, покрытая слоем серебра, которая нагревается током при откачанном воздухе. При нагревании серебро испаряется. Атомы серебра, вылетая через щель, попадают на внутреннюю поверхность второго цилиндра, давая изображение щели О. Если прибор привести во вращение вокруг общей оси цилиндров, то атомы серебра осядут не против щели, а сместятся от точки О на некоторое расстояние S. Изображение щели получается размытым. Исследуя толщину осажденного слоя, можно оценить распределение молекул по скоростям.

Зная радиусы цилиндров, их угловую скорость вращения, а также измеряя S, можно вычислить скорость движения атомов серебра при данной температуре проволоки. Результаты опыта показали, что средняя скорость атомов серебра близка к той, которая

На графике изображена зависимость числа молекул, приходящихся на единичный интервал скоростей, от скорости, которой они обладают. Максимум функции означает, что наибольшее число молекул обладает такой скоростью.

Наиболее вероятная скорость – скорость, которой обладает максимальное число молекул.

Полученное распределение справедливо для описания многих массовых процессов, характеризующихся внутренней неупорядоченностью, хаотичностью.

Средняя кинетическая энергия хаотичного поступательного движения молекул тела пропорциональна термодинамической (абсолютной) температуре:

(2)

Холодный газ отличается от нагретого до большей температуры энергией хаотичного движения молекул, поэтому хаотичное движение молекул называется .

Выразим из формулы (2) средний квадрат скорости молекул:

Умножим числитель и знаменатель правой части этого равенства на постоянную Авогадро и преобразуем выражение:

Извлекая корень квадратный из обеих частей этого равенства, получаем величину, имеющую размерность скорости и называемую средней квадратичной скоростью молекул:

Средняя квадратичная скорость, близкая по значению к средней и наиболее вероятной скоростям, дает правильное представление о значении скорости теплового движения (тепловой скорости) молекул в идеальном газе.

Пример: Вычислим тепловую скорость молекул азота при температуре .

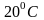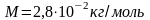
Скорость звука при той же температуре равн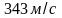а . Таким образом, тепловая скорость молекул азота, близкая к скорости пули, превышает скорость звука в 1,49 раза.