
§4. Понятие функции.
1.Области определения и значений. График функции. Сложная и обратная функции.
Если даны числовые множества X={x} и Y={y} и по некоторому закону f каждому элементу x∈X поставлен в соответствие один и только один элемент
y∈Y , то говорят, что на множестве X задана функция y=f(x), x называют аргументом функции, y — ее значением.
Через f(a) или y(a) обозначается то значение y, которое соответствует значению x=a.
Множество X называется областью определения, или областью существования функции, множество Y — областью изменения функции, или областью ее значений.
Для лучшего понимания определения функции следует познакомиться с элементами входящие в это определение.
Df. Величина «у» называется функцией переменной величины «х» если каждому значению переменной х из указанной её области изменения D(f) соответствует одно или несколько определенных значений «у».
Записывают
это так:
 х
– аргумент (независимая переменная).
Если каждому значению «х»
соответствует одно определенное значение
у,
то функцию «у»
называют однозначной.
х
– аргумент (независимая переменная).
Если каждому значению «х»
соответствует одно определенное значение
у,
то функцию «у»
называют однозначной.
Если аргумент «х» может принимать только значения действительных чисел, то функция у называется функцией действительной переменной х.
Если же каждому значению «х» соответствует несколько определенных значений у (два, три и т.д.) то функция «у» называется многозначной (двузначной, трехзначной и т.д.)
Буква
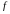 , входящая в равенство
в отличии от букв «
, входящая в равенство
в отличии от букв « »
и «
»
и «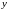 »
обозначает не переменную величину, а
то правило (закон), по которому
устанавливается соответствие между
«
»
и «
»
.
»
обозначает не переменную величину, а
то правило (закон), по которому
устанавливается соответствие между
«
»
и «
»
.
В частности, буква может обозначать совокупность математических операций, которые нужно произвести над аргументом « » чтобы получить соответствующее значение « », и указывать последовательность их выполнения.
Символ называют характеристикой функции.
Буква может обозначать не только математические операции и последовательность их выполнения, а и правило сформулированное любым способом (словами, таблицей, графиком и т.д.) по которому каждому значению « » можно найти соответствующее значение « ».
Если
функция
задана формулой
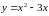 ,
то роль
здесь играет предложение:
,
то роль
здесь играет предложение:
«Чтобы получить значение , зная значения х нужно из квадрата числа вычесть утроенное это число».
Если функция y=f(x) задана аналитически (при помощи формулы), то под областью Х ее определения понимается множество тех вещественных значений аргумента x, при которых аналитическое выражение f(x) имеет смысл, т.е. выполнимы все действия, указанные в задании функции. Нахождение области определения функции, как правило, сводится к решению некоторой системы неравенств, содержащих аргумент x. Нахождение области Y значений функции производится либо преобразованием данного аналитического выражения к виду, содержащему функции, области изменения которых известны, либо к нахождению области определения функции, обратной данной.
Функция,
заданная разными формулами для различных
значений аргумента, называется
кусочно-аналитической.
Например,
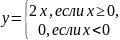
 —
кусочно-аналитическое
задание функции (эта функция может быть
задана и одной формулой y=x+│x│).
Функция знака числа x,
y=sign
x,
задается так:
—
кусочно-аналитическое
задание функции (эта функция может быть
задана и одной формулой y=x+│x│).
Функция знака числа x,
y=sign
x,
задается так:
y=
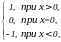
ее график изображен на рис.1.
Если
задано уравнение F
(x,
y)=0,
связывающее функцию y
и аргумент x,
то говорят, что функция y
задана
неявно.
Например, уравнение
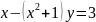
является
неявным заданием функции y.
Если разрешить это уравнение относительно
y,
то получим
 —
явное
аналитическое задание функции y.
—
явное
аналитическое задание функции y.
З а м е ч а н и е. Обычно выражение y через x при неявном задании функции не так просто, как в приведенном примере. Но при решении многих задач и не требуется выражать функцию явно.
Г рафиком
функции y=f(x)
называется геометрическое место точек
( x,
y
)
плоскости, координаты x
и
y
которых
связаны соотношением
y=f(x)
и
x
принадлежит
области определения данной функции.
Обычно графиком функции является
некоторая кривая на плоскости, а само
уравнение y=f(x)
называют
уравнением этой кривой. Напомним способы
построения графиков функций, используя
функции, графики которых известны
(таблица).
рафиком
функции y=f(x)
называется геометрическое место точек
( x,
y
)
плоскости, координаты x
и
y
которых
связаны соотношением
y=f(x)
и
x
принадлежит
области определения данной функции.
Обычно графиком функции является
некоторая кривая на плоскости, а само
уравнение y=f(x)
называют
уравнением этой кривой. Напомним способы
построения графиков функций, используя
функции, графики которых известны
(таблица).
Пусть функция z = φ(y) определена на множестве Y — множество значений некой функции y=f(x) с областью определения X; тогда переменная z является функцией от x на множестве X : z = φ(f(x)).
Функция z = φ(f(x)), аргументом которой является другая функция (точнее, функция другого аргумента), называется сложной функцией переменной x; функция y=f(x) называется внутренней, а функция z = φ(y) — внешней. Говорят также, что сложная функция является суперпозицией этих функций или что задана композиция двух функций.
Например,
функции
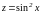 ,
,
 являются сложными функциями. Функция
может
быть представлена как
являются сложными функциями. Функция
может
быть представлена как
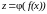 ,
где
,
где
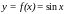 —
внутренняя
функция, а
—
внутренняя
функция, а
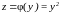 —
внешняя.
Пример сложной функции
демонстрирует «трехступенчатую»
функциональную зависимость функции z
от
аргумента x:
z=g(φ(f(x))),
где t
=
f(x)
=cos
x
—
тригонометрическая
функция; y=φ(t)
= lg
t
—
логарифмическая
функция; z=g(y)
=
—
внешняя.
Пример сложной функции
демонстрирует «трехступенчатую»
функциональную зависимость функции z
от
аргумента x:
z=g(φ(f(x))),
где t
=
f(x)
=cos
x
—
тригонометрическая
функция; y=φ(t)
= lg
t
—
логарифмическая
функция; z=g(y)
=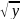 —
степенная
функция.
—
степенная
функция.
Функция y=f(x) с областью определения X и множеством значений Y называется взаимно-однозначной, если для любых х1 и х2 из области ее определения Х из неравенства х1≠х2 следует, что f(x1) ≠ f(x2), т.е. различным значениям аргумента соответствуют различные значения функции.
Примером взаимно-однозначных функций являются строго монотонные функции. Для функций, не являющихся взаимно-однозначными на всей области определения, часто удается выделить промежутки, на которых они взаимно-однозначны. Например, функция y=x2 не являются взаимно-однозначной для всех x (для x≠0 различным значениям аргумента x и –x соответствуют равные значения функции y=x2), но на промежутках (–∞; 0] и [0; +∞) она взаимно-однозначна.
Функция, определенная на множестве Y (множестве значений взаимно-однозначной функции y=f(x)), ставящая в соответствие каждому y∈Y то значение x∈X (из области определения функции y=f(x)), для которого y=f(x), называется обратной к функции y=f(x).
Для
нахождения функции (если она существует),
обратной данной y=f(x),
необходимо выразить x
через
y
:
x=
φ(y),
а затем записать полученную функцию в
обычном виде : y=f(x).
Например, обратной для функции y=2х+4
является функция y= х–2.
х–2.
Условия существования обратной функции приведены в § 2 главы III.
Область определения обратной функции совпадает с множеством значений исходной функции, и наоборот, множество значений обратной функции совпадает с областью определения исходной функции.
Графики прямой и обратной функций симметричны относительно прямой y=x.
Суперпозиция взаимно-обратных функций y=f(x) и x=f -1(y) является тождественной функцией: f(f -1(y)) = y; f(f -1(x)) = x.
Пример 1. 1) Выразить объем цилиндра, вписанного в шар радиусом R, как функцию его высоты h.
2) Имеются два куска сплава меди с серебром. В первом куске содержится p% меди, во втором — q% меди (p<q).
Задание функции |
Способ построения ее графика |
График |
1.
y = f(x)+A |
Параллельный перенос (сдвиг) графика функции y=f(x) вдоль оси OY на |A| единиц вверх, если А>0, или вниз, если A<0. (рис.2.) |
|
2. y = f(x+a) |
Параллельный перенос графика функции y = f(x) вдоль оси OX на |a| единиц влево, если a>0, или вправо, если a<0. (рис.3.)
|
|
3. y=kf(x) |
Р –1<k<0 (рис.6).
|
|
4. y=|f(x)|
|
О |
|
5. y=f (kx) |
Сжатие графика функции y=f(x) вдоль оси OX в k раз, если k>1, растяжение вдоль оси OX в 1/k раз, если 0<k<1 (рис.8), симметричное отображение относительно оси OY, если k= –1. (рис.9)
|
|
6. y=f (|x|) |
О |
|
При переплавке х кг первого сплава с у кг второго получили сплав, содержащий r % меди. Выразить зависимость у от х.
2.Четные и нечетные функции.
Функция y=f(x) называется четной, если для всех х из области ее определения выполняется равенство f( –x)= f(x).
Функция y=f(x) называется нечетной, если для всех х из области ее определения выполняется равенство f( –x)= – f(x).
Функции, не четные и не нечетные, называются функциями общего вида.
Свойства четных и нечетных функций.
Область определения четной и нечетной функций симметрична относительно начала координат.
График четной функции симметричен относительно оси координат.
График нечетной функции симметричен относительно начала координат.
Сумма, разность, произведение и частное двух четных функций с одной и той же областью определения (знаменатель дроби при этом должен быть отличен от нуля) также являются четными функциями.
Сумма и разность двух нечетных функций (с одной областью определения) есть нечетные функции.
Произведение и частное двух нечетных функций являются четными функциями.
Произведение и частное четной и нечетной функций есть нечетные функции.
При построении графиков четных и нечетных функций достаточно построить только ту часть графика, которая лежит в правой полуплоскости (при х≥0), а затем отобразить ее симметрично относительно оси ординат (для четной функции) или относительно начала координат (для нечетной функции).
Пример 2. Установить, какие из следующих функций являются четными, нечетными и какие — функциями общего вида.
y =
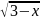 ,
2) y
=x2
+
|x|,
3)
y
=tg2x
– cos
x,
4)
y
= lg
,
2) y
=x2
+
|x|,
3)
y
=tg2x
– cos
x,
4)
y
= lg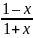 , 5)
y
= x
, 5)
y
= x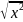 ,
,
6)
y
=
 +
+ ,
7)
y
=
,
7)
y
=
 ,
8)
y
= (2x
–1)/(
2x
+1),
9) доказать свойство 5.
,
8)
y
= (2x
–1)/(
2x
+1),
9) доказать свойство 5.
Решение
4):
Область определения функции y
= lg
,
симметрична
относительно начала координат:
x∈(–1,1).При
этом f
(–x)=
lg
=lg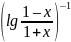 =
– lg
= –
f
(x),
следовательно, функция нечетная.
=
– lg
= –
f
(x),
следовательно, функция нечетная.

Периодические функции.
Функция y=f(x) называется периодической, если существует такое число Т>0 (не зависящее от х), что:
х+Т и х–Т также входят в область определения функции f(x);
для всех х из области определения функции выполняется равенство: f(x+Т)= f(x);
среди всех Т есть наименьшее.
Это наименьшее число Т называется периодом функции.
Свойства периодических функций.
Область определения периодической функции симметрична относительно начала координат.
Для периодической функции y=f(x) справедливо равенство f(x+kТ) = f(x), где Т — период функции, k∈Z; в частности, f(x–Т) = f(x).
Если функция y=f(x) периодическая с периодом Т, то функция y=f(ax) также периодическая с периодом Т/|a| (при a≠0).
Если функция y=f(x) периодическая с периодом Т, то функция y=f(x+a) также периодическая с периодом Т.
При построении графика периодической функции достаточно построить часть графика на интервале, равном одному периоду, а затем продолжить его на всю область определения функции.
Пример 3. Исследовать на периодичность следующие функции:
y=x2+x–1; 2) y=2; 3)y=sin
 x+1;
4) y=sin
x
– cos x;
5)y=sin
2x
–
2tg
x+1;
4) y=sin
x
– cos x;
5)y=sin
2x
–
2tg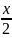 ;
6)y=cos2x;
7)y=x–|x|.
;
6)y=cos2x;
7)y=x–|x|.
Возрастающие, убывающие и ограниченные функции.
Функция y=f(x), определенная на множестве Х, называется возрастающей, если для любых х1, х2 множества Х из неравенства х1 <х2 следует, что:
f(x1)< f(x2) (1)
т.е. функция y=f(x) называется возрастающей, если большему значению ее
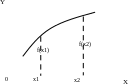
аргумента из области определения соответствует большее значение функции (рис.11)

Рис.11 Рис. 12
Функция y=f(x), определенная на множестве Х, называется убывающей, если для любых х1, х2 множества Х из неравенства х1 <х2 следует, что:
f(x1)< f(x2), (2)
т.е. функция y=f(x) называется возрастающей, если большему значению ее аргумента из области определения соответствует меньшее значение функции (рис. 12).
Возрастающие и убывающие функции называются строго монотонными.
Если в определении возрастающей функции неравенство (1) заменить на нестрогое f(x1)≤ f(x2), то такая функция называется неубывающей ( рис.13). Если в определении убывающей функции неравенство (2) заменить на нестрогое f(x1)≥ f(x2) , то такая функция называется невозрастающей (рис. 14).
Возрастающие, убывающие, невозрастающие, неубывающие функции называются монотонными функциями.
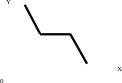

Рис.13 Рис.14
Свойства монотонных функций:
Сумма двух возрастающих (убывающих) функций есть функция возрастающая (убывающая).
Если функция y=f(x) возрастающая (убывающая), то функция y= –f(x) убывающая (возрастающая).
Если функция y=f(x) возрастающая (убывающая), то функция y= 1 / f(x)
убывающая (возрастающая) (f(x)≠0).
Суперпозиция двух монотонно возрастающих (убывающих) функций есть
монотонно возрастающая функция.
Суперпозиция двух функций, из которых одна монотонно возрастающая, а
другая монотонно убывающая, является монотонно убывающей функцией.
Функция y=f(x), определенная на множестве Х, называется ограниченной сверху на данном множестве, если существует число М такое, что f(x) ≤ М для любого х∈Х.
Функция y=f(x), определенная на множестве Х, называется ограниченной снизу, если существует число m такое, что f(x) ≥ m для любого х∈Х.
Функция y=f(x), определенная на множестве Х, называется ограниченной на данном множестве, на данном множестве, если существует число N >0 такое, что |f(x)| ≤ N для любого х∈Х. Ясно, что функция y=f(x) является ограниченной тогда и только тогда, когда она ограничена и сверху, и снизу.
Сумма и произведение ограниченных функций являются также ограниченными функциями.
Пример 4. Исследовать на монотонность следующие функции:
y = sin x на отрезке [–π/2, π/2 ]; 2) y = arctg (x2–2x+3);
y = (x2+4x+6) ln (x2+4x+6); 4) y = (1–x2)/x; 5) доказать свойство 1 для монотонно убывающих функций
Функция натурального аргумента (числовая последовательность).
Частным
случаем функции является функция
натурального аргумента y=f(n),
(n∈N),
которая обычно обозначается xn
и
называется числовой
последовательностью.
Областью определения такой функции
является множество N
натуральных чисел, а каждое значение
xn
называется
членом
последовательности.
Значению аргумента n
соответствует
число xn
,
стоящее на месте с номером n
в
этой последовательности. Последовательность
считается
заданной,
если указано правило, по которому каждому
значению аргумента n
(натуральному
числу) поставлено в соответствие
единственное значение xn.
Число xn
называется
общим членом последовательности. Для
задания последовательности достаточно
знать ее общий член, ибо, зная номер
члена последовательности, всегда можно
найти и сам член. Так, если xn=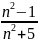 — общий член последовательности, то ее
первые члены равны 0, 3/9, 8/14, …, а, например,
десятый член x10=99/105.
— общий член последовательности, то ее
первые члены равны 0, 3/9, 8/14, …, а, например,
десятый член x10=99/105.
Если существует число m (М) такое, что для всех (n∈N) справедливо неравенство xn ≥m (xn ≤ M).
Последовательность xn называется ограниченной, если существует число L такое, что справедливо неравенство |xn| ≤ L.
Последнее определение равносильно тому, что последовательность xn ограничена и снизу и сверху.
Последовательность xn называется возрастающей (неубывающей), если для всех (n∈N) справедливо неравенство xn+1 ≥ xn, и убывающей (невозрастающей), если для всех (n∈N) справедливо неравенство xn+1 ≤ xn. Если верны соответственно строгие неравенства xn+1 > xn или xn+1 < xn, то последовательности называются строго возрастающей или строго убывающей.
Пример 5. 1) Найти формулу общего члена последовательности xn , если x1=1, а xn= xn-1 + d.
Доказать, что последовательность xn=
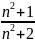 ограничена.
ограничена.Доказать, что последовательность xn = lg n – lg (n – 1) монотонна, начиная с некоторого номера n(n >1).
Найти наибольший член последовательности xn = n2/2n.
Найти наибольший член последовательности xn = n2 – 5n +1.
Доказать, что последовательность xn =
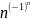 не ограничена.
не ограничена.
Найти области определения функций:
y =
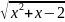 ;
2. y
= 1/(
;
2. y
= 1/(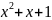 );
3. y
=
);
3. y
=
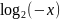 ;
;
4.
y
= ;
5. y
=
;
5. y
=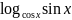 ;
6. y
=
;
6. y
=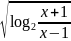 ;
;
7.
y
=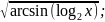 8.
y
=
8.
y
= +
+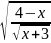 ;
9. y
=tg
;
9. y
=tg
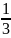 ;
;
10.
y
=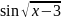 .
.
Найти множество значений функций:
y =sin2x – cos2x; 2) y =
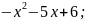 3)
y =
3)
y =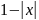 ;
;
4)
y
=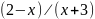 ;
5)
;
5)
 ;
6)
;
6)
 ;
;
7)
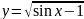 ;
8)
;
8)
 .
.
Построить графики функций:
 ;
2)
;
2)
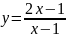 ;
3)
;
3)
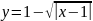 ;
4)
;
4) ;
;
5)
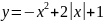 ;
6)
;
6)
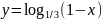 ;
7)
;
7)
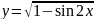 ;
;
8)
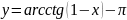 ;
9)
;
9)
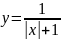 ;
10)
;
10)
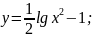
11)
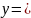 1/3)|x|;
12)
1/3)|x|;
12) ;
13)
x/2)
;
13)
x/2)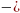 cos(x/2))2;
cos(x/2))2;
14)
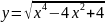 ;
15)
;
15)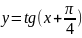 .
.
Найти суперпозиции функций
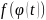 :
:
 ,
,
 ;
2)
;
2)
 ,
,
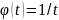 ;
;
3)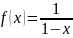 ,
,
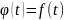 ;
4)
;
4)
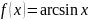 ,
,
 ;
;
5)
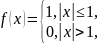 ;
;
6)
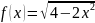 ,
,
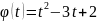 .
.
Найти функции, обратные данным:
1)
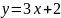 ;
2)
;
2) ;
3)
;
3)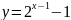 ;
4)
;
4) ;
;
5)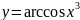 ;
6)
;
6)
 .
.
Установить, какие из следующих функций являются четными, нечетными и функциями общего вида:
1)
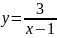 ;
2)
;
2)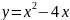 ;
3)
;
3)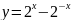 ;
4)
;
4) ;
;
5)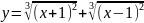 ;
6)
;
6)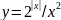 ;
7)
;
7) ;
;
8)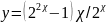 ;
;
9) доказать свойства 4) –7) четных и нечетных функций;
10) доказать, что любую функцию с областью определения, симметричной относительно начала координат, можно представить в виде суммы четной и нечетной функций.
Исследовать на периодичность следующие функции:
1)
 ;
2)
;
2) ;
3)
;
3) ;
;
4) ;
5)
sin4
x
– sin4
x;
6)
;
5)
sin4
x
– sin4
x;
6)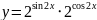 ;
;
7)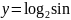 2
x;
8)
2
x;
8)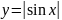 .
.
Исследовать на монотонность следующие функции:
1)
 2)
2)
 ;
3)
;
3)
4)
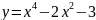 ;
5)
;
5)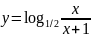 ;
6)
;
6)
 .
.
Установить, являются ли ограниченными следующие функции:
1)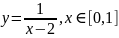 ;
2)
;
2)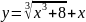 ;
;
3) ;
4)
;
4) ;
;
5) ;
6)
;
6)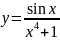 .
.
Доказать, что последовательность ограничена:
1) ;
2)
;
2) ;
3)
;
3) .
.
Найти наибольший член последовательности:
1)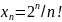 2)
2) ;
3)
;
3)
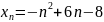 .
.
Найти формулу общего члена последовательности
 :
:
 ,
,
 .
.
Найти наименьший член последовательности:
1)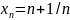 ;
2)
;
2)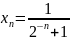 ;
3)
;
3) .
.
Доказать, что последовательность не является ограниченной:
1) ;
2)
;
2)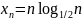 ;
3)
;
3)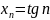 .
.
Доказать, что последовательность монотонна:
1)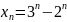 ;
2)
;
2)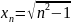 ;
3)
;
3)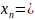
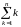 .
.

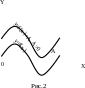

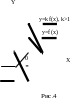
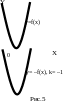
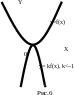 астяжение
вдоль оси OY
в k
раз, если
k>1,
или сжатие в 1/k
раз, если
0<k<0
(рис.4). Симметричное отображение
графика y=f(x)относительно
оси OX, если
k=–1(рис.5).
Растяжение в |k|
раз и симметричное отображение
относительно оси OX
при k<–1;
сжатие в 1/|k|
раз и симметричное отображение
относительно оси OX
при
астяжение
вдоль оси OY
в k
раз, если
k>1,
или сжатие в 1/k
раз, если
0<k<0
(рис.4). Симметричное отображение
графика y=f(x)относительно
оси OX, если
k=–1(рис.5).
Растяжение в |k|
раз и симметричное отображение
относительно оси OX
при k<–1;
сжатие в 1/|k|
раз и симметричное отображение
относительно оси OX
при
 ставить
без изменений часть графика y=f(x),
лежащую выше оси OX,
а остальную часть графика (расположенную
ниже оси ОХ)
отобразить относительно оси абсцисс
(рис.7).
ставить
без изменений часть графика y=f(x),
лежащую выше оси OX,
а остальную часть графика (расположенную
ниже оси ОХ)
отобразить относительно оси абсцисс
(рис.7).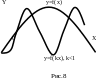

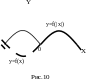 тбросить
часть графика y=f(x),
лежащую в левой полуплоскости; остальную
часть графика (лежащую в правой
полуплоскости) сохранить и, кроме
того, отобразить относительно оси OY
(рис.10).
тбросить
часть графика y=f(x),
лежащую в левой полуплоскости; остальную
часть графика (лежащую в правой
полуплоскости) сохранить и, кроме
того, отобразить относительно оси OY
(рис.10).