
Глава I
МНОЖЕСТВА И ФУНКЦИИ
§1. Понятие множества, подмножества, включения
Множество относится к простейшим, неопределяемым понятиям и понимается как собрание, совокупность, коллекция объектов, объединяемых по какому-то правилу (характеристическому свойству).
Множество считается заданным, если каким-либо образом указаны все его элементы. Задание множества производится или перечислением его элементов, или указанием характеристического свойства.
Множества
обозначаются обычно большими буквами
латинского алфавита, его элементы —
маленькими. В случае, когда элемент x
принадлежит
множеству A,
пишут
x∈A,
в противном случае x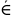 A
(или x
∉
A).
A
(или x
∉
A).
Множество,
не содержащее элементов, называется
пустым
и обозначается символом
![]() .
.
В том случае, когда два множества A и B состоят из одних и тех же элементов, говорят, что они равны, и пишут A=B, в противном случае A≠B. Для доказательства равенства двух множеств достаточно показать, что каждый элемент первого множества принадлежит второму и обратно, что каждый элемент второго множества принадлежит первому.
Если каждый элемент множества А является элементом множества В, то множество А называется подмножеством множества В, что обозначается так: А⊆В. Всякое непустое множество А имеет по крайней мере два подмножества: само множество А и пустое множество , которые называются несобственными подмножествами множества А. Запись А⊂В означает, что множество А является подмножеством множества В, но A≠B. В этом случае говорят, что множество А есть собственное подмножество множества В.
Множество J называется универсальным множеством для системы множеств А, В, С, …, если каждое из этих множеств является его подмножеством.
Пример 1. Составить список элементов множества
А = {x: x∈N, –3<x ≤ 5}.
Пример 2. Описать множество точек М числовой прямой, таких, что
{М: │ОМ │= 1}, и перечислить его элементы.
Пример 3. Верно ли соотношение {a, b, c} = {{a, b}, c}?
Пример 4.
Составить список элементов множеств, заданных характеристическими свойствами: 1) А= {x : x2 – 8 x+15=0 }; 2) А = { x: x∈N,
–11<x ≤–3}.
Доказать, что если А= {x : x2 – 7 x+6=0 } и В={1, 6}, то А=В.
Описать множества точек М плоскости, таких, что: 1) {М: │ОМ │= R};
2) {М: │ОМ │≤ R}; 3) {М: │АМ │= │ВМ │}, где А и В — заданные точки.
4. Какая разница в записях А⊂В и А∈В?
5. Доказать, что {{1, 2}, {2, 3}}≠{1, 2, 3}.
6. Верно ли, что {1, 2}∈ {{1, 2, 3}, {1, 3}, 1, 2}? Верно ли, что {1, 2}⊆{{1, 2, 3}, {1, 3}, {1, 2}?
7. Привести примеры таких множеств А, В и С, что: 1) А∈В, В∈С, А С ;
2)А⊆В, В⊆С, А⊆С; 3) А∈В, А⊂В.
8. Является ли множество, состоящее из числа 0, пустым?
9.
Доказать справедливость соотношения:
![]() ≠ {
}.
≠ {
}.
10. Доказать, что существует только одно множество, не имеющее элементов.
11. Найти все подмножества множеств: 1) ; 2) { }; 3) {1, 2}; 4) {a, b, c, d}.
12. Доказать, что если А⊆В, В⊆А, то А=В, и обратно, если А=В, то А⊆В, В⊆А.
§2. Операции над множествами
Объединением
А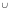 В
множеств А
и
В
называется множество, состоящее из
элементов, входящих в множества А
и
В,
и только из них, т.е. А
В
={x
: x∈A
или
x∈В}.
В
множеств А
и
В
называется множество, состоящее из
элементов, входящих в множества А
и
В,
и только из них, т.е. А
В
={x
: x∈A
или
x∈В}.
Е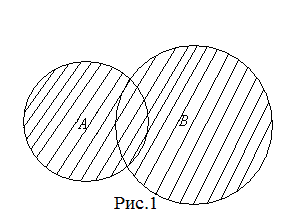
 сли
один и тот же элемент содержится и во
множестве А
и
во множестве В,
то в их объединение он входит только
один раз. Схематически объединение
множеств А
и В
изображено
на рис.1.
сли
один и тот же элемент содержится и во
множестве А
и
во множестве В,
то в их объединение он входит только
один раз. Схематически объединение
множеств А
и В
изображено
на рис.1.
Объединением
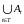 множеств
At
(t∈T)
называется множество, состоящее из
элементов, входящих в множества At
(t∈T),
и только из них (здесь предполагается,
что индекс t
пробегает
все значения из некоторого множества
T.
множеств
At
(t∈T)
называется множество, состоящее из
элементов, входящих в множества At
(t∈T),
и только из них (здесь предполагается,
что индекс t
пробегает
все значения из некоторого множества
T.
Пересечением
А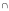 В
множеств
А
и
В
называется
множество, состоящее из элементов,
принадлежащих как множеству А,
так и множеству В,
и только из них, т.е. А
В={x
:
x∈A
и
x∈B}.
Схематически пересечение множеств А
и
В
изображено
на рис.2.
В
множеств
А
и
В
называется
множество, состоящее из элементов,
принадлежащих как множеству А,
так и множеству В,
и только из них, т.е. А
В={x
:
x∈A
и
x∈B}.
Схематически пересечение множеств А
и
В
изображено
на рис.2.
Пересечением
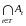 множеств
At
(t∈T)
называется множество, состоящее из
элементов, принадлежащих множествам
At
(t∈T),
и только их них.
множеств
At
(t∈T)
называется множество, состоящее из
элементов, принадлежащих множествам
At
(t∈T),
и только их них.
Если пересечение множеств не является пустым, то множества называют пересекающимися.
Р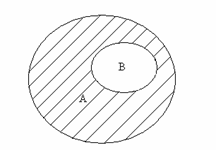 азностью
А∖В
множеств
А
и В
называется множество, состоящее из
элементов множества А,
не входящих в множество В,
и только из них, т.е.
азностью
А∖В
множеств
А
и В
называется множество, состоящее из
элементов множества А,
не входящих в множество В,
и только из них, т.е.
А∖В={ x : x∈А и x∈В }. Схематически разность множеств А и В изображена на рис.3.

Рис.3.
Разность
J∖B,
где J
— универсальное
множество, называется дополнением
множества
В
и
обозначается
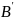 .
.
Пример 1. Доказать тождество А А= А А=А.
Пример
2. Доказать,
что если Аt⊆B
для
всех t∈T,
то
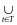 At⊆В.
At⊆В.
Пример 3. Доказать, что если А⊆В С, то А ⊆С, и обратно.
Пример 4. В каком из отношений (X ⊂Y, X ⊃Y, X=Y) находятся множества X и Y, если: 1) X= А (В∖С), Y= (А В) ∖ (А С); 2) X= (А В) ∖ С; Y= (А∖С) (В ∖С); 3) X= А ∖ (В С), Y= (А∖В) (А∖С).
Пример
5. Доказать,
что: 1) для всех t∈T,
В⊆Аt
,
то В⊆
;
2) если для всех t∈T
Аt⊆Вi,
то
⊆ и
⊆
и
⊆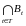 ;
3)
∖
=
;
3)
∖
=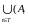 ∖
Вt);
∖
Вt);
4) есть наименьшее множество, включающее все множества Аt; 5) есть наименьшее множество, содержащееся во всех множествах Аt.
