Задачи по темам для экзамена
Простые процентные ставки
Задача 1. Первоначальная сумма 5000 руб. помещена в банк на 2 года под 15% годовых. Найти наращенную сумму.
Решение:
FV=5000(1+0.15*2)=6500 руб.
Задача 2. Первоначальная сумма 7000 руб. помещена в банк на 0,5 года под 10% годовых. Найти наращенную сумму.
где t – число дней проведения операции;
B – временная база (число дней в году: 360, 365 или 366).
Решение:
FV=7000(1+0.10*0.5)=7335 руб.
Задача 3. Первоначальная сумма 3000 руб., наращенная сумма 4500 руб., ставка – 20 % годовых. Найти период начисления.
Выражаем:
Решение:
n = ( 4500/3000 - 1 )*1/0.20=2,5 года
Задача 4. Первоначальная сумма 6000 руб., наращенная сумма 7200 руб., ставка – 10 % годовых. Найти период начисления.
Решение:
n = ( 7200/6000 - 1 )*1/0.10=2 года
Задача 5. Первоначальная сумма 2000 руб., наращенная сумма 2200 руб., период начисления – 0,5 года. Найти простую процентную ставку.
Выражаем:
Решение:
r =( 2200/2000-1 )*1/0,5=0,2 =20%
Задача 6. Первоначальная сумма 3000 руб., наращенная сумма 3300 руб., период начисления – 0,5 года. Найти простую процентную ставку.
Выражаем:
Решение:
r =(3300/3000-1 )*1/0,5=0,2 =20%
Математическое дисконтирование
Задача 7. Наращенная сумма 7000 руб., период начисления – 0,25 года, простая процентная ставка – 12 % годовых. Найти первоначальную сумму.
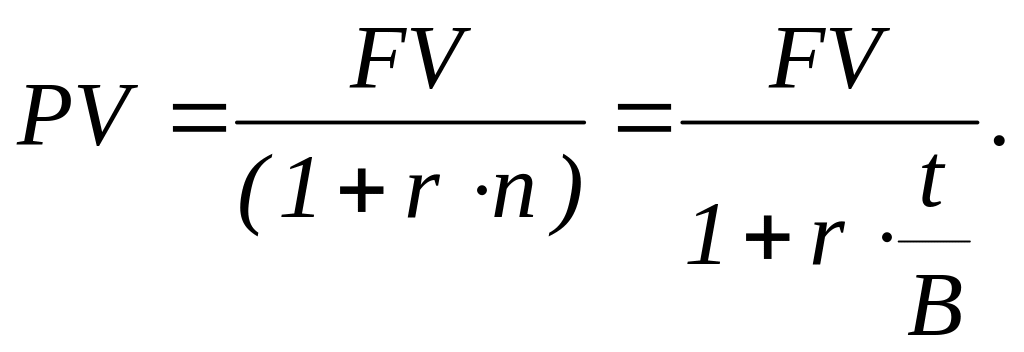
Решение:
PV=7000/(1+0.12*0.25)=6796,12 руб. ~ 6796 руб. (уменьш. т.к. дисконтирование)
Задача 8. Наращенная сумма 6000 руб., период начисления – 0,5 года, простая процентная ставка – 15 % годовых. Найти первоначальную сумму.
Решение:
PV=6000/(1+0,15*0,5)=5581,4 руб. ~ 5581 руб. (уменьш. т.к. дисконтирование)
Случай изменения простой ставки ссудного процента
Задача 9. Первоначальная сумма 3000 руб. В первой половине года применялась процентная ставка – 15% годовых, во второй половине года использовалась ставка -12% годовых. Найти наращенную стоимость.
Решение:
FV=3000*(1+0,15*0,5+0,12*0,5)=3405 руб.
Задача 10. Первоначальная сумма 4000 руб. В первой половине года применялась процентная ставка – 11% годовых, во второй половине года использовалась ставка – 14% годовых. Найти наращенную стоимость.
Решение:
FV=4000*(1+0,11*0,5+0,14*0,5)= 4500 руб.
Сложные процентные ставки
Задача 11. Первоначальная сумма 5000 руб. помещена в банк на 2 года под 15% годовых. Найти наращенную сумму.
Решение:
FV2=5000*(1+0,15)2=6612,5 руб.
Задача 12. Первоначальная сумма 7000 руб. помещена в банк на 3 года под 10% годовых. Найти наращенную сумму.
Решение:
FV3=7000*(1+0,10)3=9317 руб.
Задача 13. Первоначальная сумма 3000 руб., наращенная сумма 4500 руб., ставка – 20% годовых. Найти период начисления.
Выражаем:
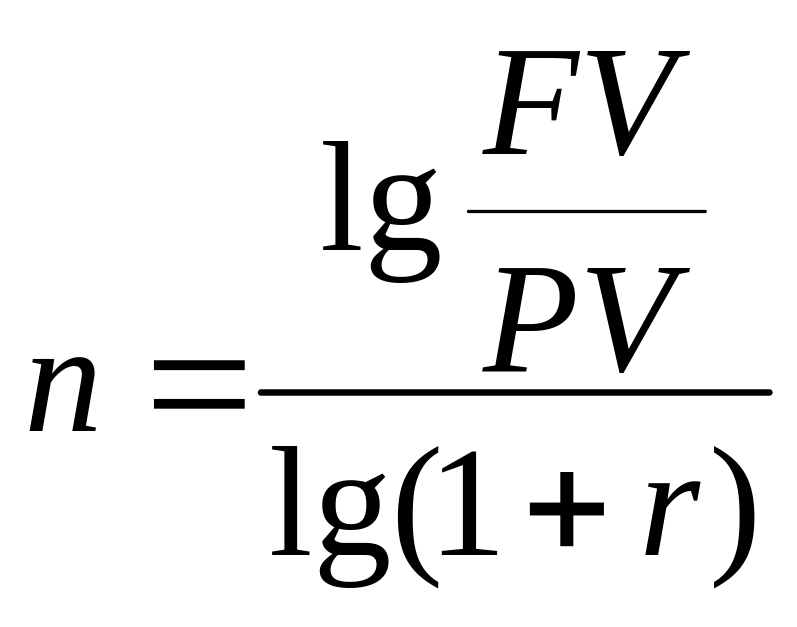
Решение:
n=lg(4500/3000)/lg(1+0,20)=2,2239 года.
Задача 14. Первоначальная сумма 6000 руб., наращенная сумма 7200 руб., ставка – 10% годовых. Найти период начисления.
Решение:
n=lg(7200/6000)/lg(1+0,10)=1,913 года.
Задача 15. Первоначальная сумма 2000 руб., наращенная сумма 3500 руб., период начисления 3 года. Найти сложную процентную ставку.
Решение:
Задача 16. Первоначальная сумма 3000 руб., наращенная сумма 4000 руб., период начисления 2 года. Найти сложную процентную ставку.
Решение:
Задача 17. Наращенная сумма 7000 руб., период начисления 2 года, сложная ставка процента 12% годовых. Найти первоначальную сумму.
Выражаем:
Решение:
PV=7000/(1+0.12)2=5580,46 руб.
Задача 18. Наращенная сумма 6000 руб., период начисления 3 года, сложная ставка процента 15% годовых. Найти первоначальную сумму.
Решение:
PV=6000/(1+0.15)3=3945,1 руб.
Случай изменения сложной процентной ставки
Задача 19. Первоначальная сумма 3000 руб., 2 года применялась сложная процентная ставка 15% годовых, затем 3 года применялась сложная процентная ставка 12% годовых. Найти наращенную сумму.
Решение:
FV=3000*(1+0.15)2*(1+0.12)3=5574.05 руб.
Задача 20. Первоначальная сумма 4000 руб., 3 года применялась сложная процентная ставка 11% годовых, затем 2 года применялась сложная процентная ставка 14% годовых. Найти наращенную сумму.
Решение:
FV=4000*(1+0.11)3*(1+0.14)2=7109,49 руб.
Начисление сложных процентов несколько раз в году
Задача 21. Первоначальная сумма 7000 руб., период начисления 3 года, сложная процентная ставка 12% годовых с начислением ежеквартально. Найти наращенную сумму.
где m – число периодов начисления в году.
Решение:
m=4 - в году 4 квартала
FV=7000*(1+0,12/4)3*4=9980,33 руб.
Задача 22. Первоначальная сумма 6000 руб., период начисления 3 года, сложная процентная ставка 12% годовых с начислением ежемесячно. Найти наращенную сумму.
где m – число периодов начисления в году.
Решение:
m=12 - в году 12 месяцев
FV=6000*(1+0,12/12)3*12=8584,61 руб.
Задача 23. Первоначальная сумма 7000 руб., период начисления 2 года, сложная процентная ставка 12% годовых. Начисление процентов происходит непрерывно. Найти наращенную сумму.
Решение:
FV=7000*e2*0.12=8898,74 руб.
Сравнение операций
Задача 24. Какой вариант инвестирования первоначальной суммы на 3 года лучше: под простую процентную ставку 18% годовых или под сложную процентную ставку 15 % годовых.
Решение:
rп = ((1+0,15)3-1)*1/3=0,1736~17,4%<0,18 (простая лучше)
Задача 25. Какой вариант инвестирования первоначальной суммы на 2 года лучше: под простую процентную ставку 17% годовых или под сложную процентную ставку 15,5 % годовых.
Решение:
rп = ((1+0,155)2-1)*1/2=0,167~16,7% < 0,17 (простая лучше)
Задача 26. Какой вариант инвестирования первоначальной суммы на 3 года лучше: под простую процентную ставку 18% годовых или под сложную процентную ставку 15% ежеквартально.
Решение:
rп = ((1+0,15/4)3*4-1)*1/3=0,185~18,5% >0,18 (сложная лучше)
Задача 27. Какой вариант инвестирования первоначальной суммы на 2 года лучше: под простую процентную ставку 19% годовых или под сложную процентную ставку 14% ежемесячно.
Решение:
rп =((1+0,14/12)2*12-1)*1/2=0,160~16,0% <0,19 (простая лучше)
Задача 28. Найти эффективную годовую ставку сложных процентов, эквивалентную сложной процентной ставке 10 % годовых ежеквартально.
Решение:
rсл =((1+0,10/4)4-1=0,104~10,4%
Вместо начисления каждый квартал 2,5% можно один раз в год начислять 10,4%.
Задача 29. Найти эффективную годовую ставку сложных процентов, эквивалентную сложной процентной ставке 12 % годовых ежеквартально.
Решение:
rсл =((1+0,12/4)4-1=0,125~12,5%
Вместо начисления каждый квартал 3% можно один раз в год начислять 12,5%.
Задача 30. Найти годовую номинальную сложную процентную ставку (проценты начисляются каждый месяц), эквивалентную сложной процентной ставке 15 % годовых.
Решение:
r =12* ((1+0,15)1/12-1)=0,1406~14,1%
Вместо начисления один раз в год 15% можно начислять каждый месяц 14,1/12=1,175%
Задача 31. Найти годовую номинальную сложную процентную ставку (проценты начисляются каждый месяц), эквивалентную сложной процентной ставке 20 % годовых.
Решение:
r =12* ((1+0,20)1/12-1)=0,1837~18,4%
Вместо начисления один раз в год 20% можно начислять каждый месяц 18,4/12=1,53%
Простые учетные ставки
Задача 32. Кредит 7000 руб. выдается на 0,5 года по простой учетной ставке 11 % годовых. Какую сумму получит заемщик.
Решение:
P =7000* (1-0,5*0,11)=6615 руб.
Задача 33. Кредит 8000 руб. выдается на 0,25 года по простой учетной ставке 12 % годовых. Какую сумму получит заемщик.
Решение:
P =8000* (1-0,25*0,12)=7760 руб.
Задача 34. Вексель на сумму 20000 руб. с датой погашения 27 ноября 2007 г. был учтен банком 11 августа 2007 г. по простой учетной ставке 12% годовых. Продолжительность года 365 дней. Определить, какая сумма была выплачена банком.
Решение:
t=21 (август) + 30 (сентябрь)+31 (октябряь)+ 27 (ноябрь) - 1 день = 108 дней.
P =20000* (1-0,12*108/365)=19289,86 руб.
Задача 35. Вексель на сумму 15000 руб. с датой погашения 25 октября 2007 г. был учтен банком 9 сентября 2007 г. по простой учетной ставке 15% годовых. Продолжительность года 365 дней. Определить, какая сумма была выплачена банком.
Решение:
P =15000* (1-0,15*46/365)=14716,44 руб.
Задача 36. Вексель учтен банком за 0,5 года до даты погашения по простой учетной ставке 14% годовых. Банк выплатил сумму 15000 руб. Определить номинальную стоимость векселя.
Выражаем:
Решение:
F=15000/(1-0,5*0,14)=16129,03 руб.
Задача 37. Вексель учтен банком за 0,25 года до даты погашения по простой учетной ставке 15% годовых. Банк выплатил сумму 7000 руб. Определить номинальную стоимость векселя.
Решение:
F=7000/(1-0,25*0,15)=7272,73 руб.
Задача 38. Вексель номинальной стоимостью 12000 руб. учтен банком за 0,5 года до даты погашения. Банк выплатил сумму 11500 руб. Определите простую учетную ставку.
Выражаем:
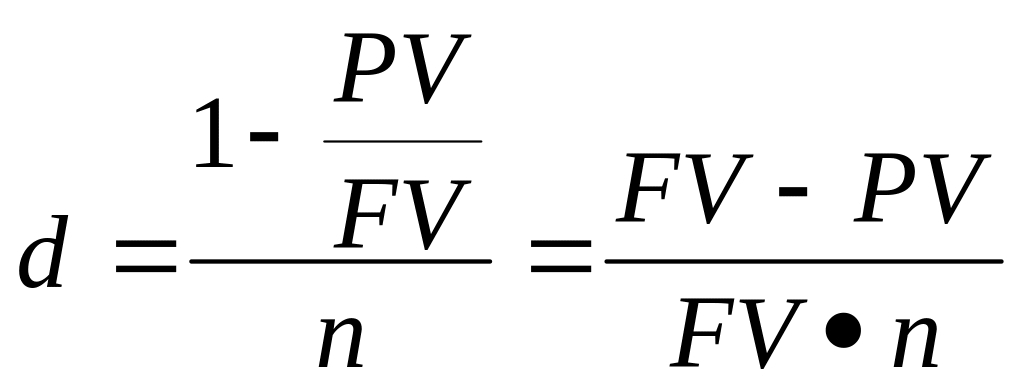
Решение:
d=(12000-11500)/(0,5*12000)=0,083 ~8% годовых
Задача 39. Вексель номинальной стоимостью 10000 руб. учтен банком за 0,25 года до даты погашения. Банк выплатил сумму 9600 руб. Определите простую учетную ставку.
Решение:
d=(10000-9600)/(0,25*10000)=0,16 ~16% годовых
Задача 40. Кредит 9000 руб. выдается по простой учетной ставке 12% годовых. Заемщик получил сумму 8000 руб. Продолжительность года 365 дней. Определить, на какой срок был выдан кредит.
Выражаем:
где К=365 дней (продолжительность года)
Решение:
t=365*(9000-8000)/(0,12*9000)=337,96 ~338 дней.
Задача 41. Кредит 11000 руб. выдается по простой учетной ставке 14% годовых. Заемщик получил сумму 10500 руб. Продолжительность года 365 дней. Определить, на какой срок был выдан кредит.
где К=365 дней (продолжительность года)
Решение:
t=365*(11000-10500)/(0,14*11000)=118,51 ~119 дней.