
- •2. Современные подходы механики разрушения к оценке устойчивости стеклообразных полимеров к образованию и росту трещин
- •2.1. Классические аналитические методы макромеханики трещин.
- •2.1.1. Энергетические параметры трещинодвижущих сил и трещиностойкости в лумр.
- •2.1.2. Силовые параметры трещинодвижущих сил и трещиностойкости в лумр
- •2.2. Методы нелинейно-упругой механики разрушения (нумр)
- •2.2.1. Глобальные энергетические j-параметры трещинодвижущих сил и трещиностойкости в нумр.
2.2. Методы нелинейно-упругой механики разрушения (нумр)
В большом числе случаев поведение полимерных матриц армированных композитов и полимерных клеевых слоев значительно отклоняется от линейной упругости и псевдо-хрупкого разрушения вследствие резкого проявления вязко-упругости, вынужденной эластичности или пластичности полимера с развитием большой зоны неупругих деформаций вблизи вершины трещины. При этом методы ЛУМР не применимы и требуются другие подходы, важнейшим из которых связан с введением в качестве энергетического параметра трещинодвижущей силы максимального потока энергии через произвольный замкнутый контур, окружающий вершину трещины (J-параметра), применимого в случае резко выраженного локального или глобального нелинейно-упругого, в частности, упруго-пластического поведения материала с трещиной.
2.2.1. Глобальные энергетические j-параметры трещинодвижущих сил и трещиностойкости в нумр.
J-параметр трещинодвижущих сил определяется как изменение потенциальной энергии деформирования тела с трещиной при ее прорастании при монотонном нагружении. Его критическое значение (Jc), которое, как и критическое значение G-параметра (Gc), соответствует началу роста трещин, характеризует трещиностойкость (работу разрушения) материала, равно энергии, затрачиваемой на образование единицы площади поверхности при росте трещины и имеет размерность Дж/м2. При малой величине зоны неупругих деформаций вблизи вершины трещины, т.е. для линейно-упругого деформирования и псевдо-хрупкого разрушения, J и Jc равны G и Gc соответственно.
Введение
J
и JС
параметров
трещинодвижущих
сил и трещиностойкости в
НУМР
базируется на анализе глобального
баланса энергии в любой по величине
области, окружающей вершину трещины,
размеры которой ограничиваются только
размерами тела. J-параметр
представляет собой обобщенный
энергетический параметр трещинодвижущей
силы, характеризующий поток энергии
через
произвольный замкнутый контур, окружающий
вершину трещины, и равен не
зависящему от пути интегрирования
энергетическому контурному интегралу,
или интегралу Черепанова–Райса. Он
представляет собой интенсивность
высвобождения энергии деформирования
при образовании трещины в нелинейно-упругом
материале при монотонном нагружении:
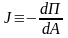 ,
где Π - потенциальная
энергия, равная разности накопленной
в теле энергии деформирования и работы,
совершенной внешними силами; А – площадь
поверхностей трещины. Размерность
J-интеграла
,
где Π - потенциальная
энергия, равная разности накопленной
в теле энергии деформирования и работы,
совершенной внешними силами; А – площадь
поверхностей трещины. Размерность
J-интеграла
 =энергия/площадь.
=энергия/площадь.
В
отличие от G-параметра
J-интеграл
может быть рассчитан при любых размерах
зоны неупругих деформаций вблизи кончика
трещины, которая может быть распространена
до самого края тела, т.е. при нарушении
его глобальной линейной упругости
(Рис.2.9).
В
самом общем виде он определяется
выражением:
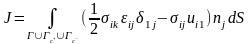 (2.18а),
где
(2.18а),
где
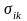 ,
,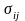 ,
,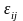 -тензоры
общих напряжений и деформаций при
растяжении в области, ограниченной
контуром Г;
-тензоры
общих напряжений и деформаций при
растяжении в области, ограниченной
контуром Г;
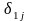 ,
,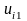 -
тензоры локального смещения трещины в
направлении у
и х
соответственно; nj-
единичный вектор, нормальный к контуру
Г;
dS-
малый элемент контура
Г.
-
тензоры локального смещения трещины в
направлении у
и х
соответственно; nj-
единичный вектор, нормальный к контуру
Г;
dS-
малый элемент контура
Г.


Рис.2.9. Локальные координаты контурного интеграла.
В
случае плоского контура вокруг трещины
с локальными координатами, приведенными
на рис.2.9, J-интеграл
равен:
 (2.18б),
где
Г
- произвольный замкнутый контур,
окружающий вершину трещины, вдоль
которого осуществляется интегрирование
в направлении против часовой стрелки,
начиная с нижней плоской поверхности
трещины и заканчивая верхней;
(2.18б),
где
Г
- произвольный замкнутый контур,
окружающий вершину трещины, вдоль
которого осуществляется интегрирование
в направлении против часовой стрелки,
начиная с нижней плоской поверхности
трещины и заканчивая верхней;
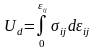 - плотность
энергии деформирования; Ti=σijnj
- вектор распределенных по границам
контура
Г
усилий.
При учете нормальных и сдвиговых
напряжений и смещений относительно оси
х
(σn,
σs,
un,us
соответственно) J-интеграл
имеет вид:
- плотность
энергии деформирования; Ti=σijnj
- вектор распределенных по границам
контура
Г
усилий.
При учете нормальных и сдвиговых
напряжений и смещений относительно оси
х
(σn,
σs,
un,us
соответственно) J-интеграл
имеет вид:
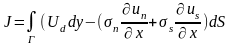 (2.18в).
(2.18в).
Таким образом, величина J-интеграла не зависит от формы и размера замкнутого контура Г и аналогично параметру G характеризует интенсивность высвобождения накопленной энергии упругого деформирования при увеличении длины трещины. В отсутствие интенсивного пластического деформирования в вершине трещины, т.е. в случае в линейно-упругих псевдо-хрупких материалов, параметр J равен G. Однако J-параметр позволяет характеризовать интенсивность высвобождения упругой энергии при росте трещин в упруго-пластичных материалах с ярко выраженной пластичностью (большой зоной неупругих деформаций вблизи вершины трещины), для которых G-параметр не применим. Он также более эффективно, чем G, может применен в случае анизотропных гетерогенных материалов, в том числе с высокой пластичностью. В общем, J параметр является более универсальным энергетическим параметром, чем G.
