2. Современные подходы механики разрушения к оценке устойчивости стеклообразных полимеров к образованию и росту трещин

В современной механике материалов и конструкций при оценке их устойчивости к разрушению выделяются подходы критериальной механики разрушения с использованием глобальных (макромеханических) и локальных (микромеханических) критериев разрушения материалов, механики повреждений со статистической оценкой степени повреждения материалов в результате накопления микроповреждений и механики трещин с анализом условий инициирования и роста возникающего или существующего макроскопического дефекта (трещины). В настоящее время применительно к слоистым армированным ПКМ и адгезионным соединениям с резко выраженной гетерогенностью и анизотропией структуры и свойств механика трещин рассматривается как эффективный подход к оценке статической и усталостной устойчивости к повреждениям типа расслоения или отслоения и, соответственно, остаточной прочности и живучести конструкций на их основе при заданном типе дефектов и условиях нагружения и деформирования. При этом в механике трещин решаются две принципиально различные задачи:

1) определение параметров, характеризующих нагрузку (движущую силу) на существующую стационарную и достаточно большую, фиксируемую неразрушающими методами контроля трещину в монотонно нагружаемом материале и критических условий начала роста (страгивания, раскрытия) заданной трещины, определяемых равенством или превышением трещинодвижущей силой сопротивления росту трещины (трещиностойкости) материала. Под монотонным понимают такой вид нагружения, при котором внешняя нагрузка возрастает постепенно с постоянной скоростью вплоть до достижения критических условий. Отдельной задачей при этом является определение условий возникновения и критического роста трещины в местах концентрации напряжений;

2) анализ поведения (возникновения и докритического роста) трещин в условиях статических и циклических усталостных нагрузок, меньших критических.

Эти задачи решаются, в первую очередь, классическими аналитическими и экспериментальными методами линейной и нелинейной упругой механики разрушения (ЛУМР и НУМР) при трех типах статических нагрузок на заданную трещину (Рис.2.1). I II III I II III

Рис.2.1. Типы (моды) нагрузок на края (берега) трещины и ее развития: I – растяжение (раскрытие); II – сдвиг в плоскости; III –сдвиг в антиплоскости (срез).

2.1. Классические аналитические методы макромеханики трещин.

Эти методы базируются на анализе баланса энергии и распределения напряжений при нагружении однородного (изотроп­ного) линейно-упругого твердого тела с заданной трещиной до начала (инициирования) ее равновесного обратимого роста и определении, соответственно, энергетических и силовых параметров трещинодвижущих сил и трещиностойкости с учетом геометрии (формы и размеров) тела и трещины и упругих свойств материала.

2.1.1. Энергетические параметры трещинодвижущих сил и трещиностойкости в лумр.

Введение энергетических параметров трещинодвижущих сил и трещиностойкости в ЛУМР базируется на концепции Гриффита, в соот­ветствии с которой равновесный обратимый процесс распространения заданной трещины в идеально упругом теле в изотермических усло­виях при отсутствии влияния окружающей среды возможен, если энергия, накапливаемая при упру­гом деформировании твердого тела достаточна для образования двух новых поверхностей при распространении трещины. Простейшей моделью служит нагружаемая растяжением бесконеч­ная пластина из гомогенного изотропного линейно-упругого мате­риала единичной толщины с эллипти­ческой центральной трещиной с острыми краями, раскрываемая по моде I (Рис.2.2). При этом предполагается, что рост (удлинение) трещины происходит в направлении ее первоначальной ориентации, т.е. тре­щина является себе подобной.

Рис.2.2. Схема бесконеч­ной пластины из однородного и изотропного линейно-упругого мате­риала единичной толщины с эллипти­ческой центральной трещиной, растягиваемой глобальным на­пряжением σ вдали от трещины в направлении, перпендикулярном ее основной оси х.

Условие энергетического баланса соответствует равенству уменьшения накопленной энергии упругого деформирования (U) затрачиваемой работе (W) при бесконечно малом увеличении длины трещины a: 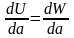(2.1). В общем случае баланс энергии (2.1) не зависит от типа нагружения трещины (I, II или III) и способа приложения внешних сил.

Основываясь на расчетах локальных напряжений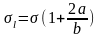 (2.2) вдоль основной оси вблизи кончика эллипти­ческой центральной трещины длиной 2а в бесконеч­ной пластине из однородного и изотропного линейно-упругого мате­риала единичной толщины, растягиваемой удаленным от трещины на­пряжением σ в направлении, перпендикулярном ее оси (см. Рис.2.2), выполненных Инглисом, Гриффит показал, что величина (2.3а), где Е - модуль упругости материала. В предположении, что энергия, затрачиваемая на образование двух новых поверхностей при росте трещины, равна удвоенной поверхностной энергии твердого тела γ_т: (2.3б) из баланса (2.1) следует известная фор­мула Гриффита для предела прочности изотропной пластины с центральным дефектом размером 2а или краевым дефектом размером а: (2.4). Позднее величина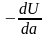 (2.5) была обозначена Ирвином как 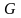, названа ин­тенсивностью высвобождения энергии упругой деформации при обратимом равновесном развитии трещины и введена в качестве обобщенной характеристики трещинодвижущей силы - G-параметра с размерностью в системе СИ [Дж/м²] (Рис.2.3).

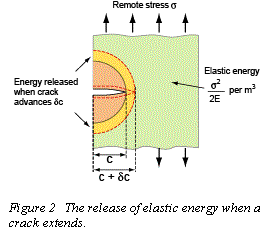
Рис.2.3. Схематическое изображение упругой энергии, высвобождающейся при росте трещины в линейно-упругом материале.(Energy released when crack advances δc –энергия, высвобождающаяся при продвижении трещины на величину δc; Remote stress σ – удаленное напряжение σ ;Elastic energy per m² – накопленная упругая энергия на м²).

Для указания конкретного типа (моды) нагружения трещины параметр G используется с индексом М (G_М,), соответствующим римским цифрам I, II, III (см. рис.2.1). При комбинированных нагрузках на трещину указывается сочетание мод, например, G_I-II. В случае сложно-напряженного состояния трехмерного тела, в котором на трещину воздействуют все три типа нагрузок, общий G-параметр является суммой отдельных параметров: G = G_I+Gii + G_III (2.6). При простых типах нагружения трещины в линейно-упргом теле трещинодвижущие силы G_I, Gii и G_III пропорциональны квадрату прило­женного напряжения σ или τ, длине трещины а и обратно пропорциональны модулю упругости материала Е: 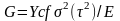(2.7), где Y - геометрический фактор, учитывающий форму и размеры тела (образца, элемента конструкции) и дефекта в нем, а также характер его нагружения, с - константа, учитывающая эффект Пуассона и равная при плоском напряженном состоянии 1, при плоской де­формации и нагружении по типу I или II 1-v², а при нагружении по типу III 1+v (v- коэффи­циент Пуассона).

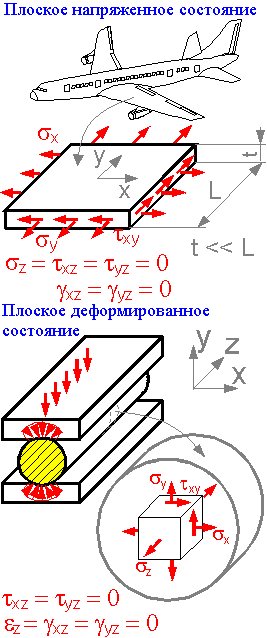
(Примечание: При плоском напряженном состоянии только  четыре компонента тензора деформаций (ε_x, ε_y, ε_z, γ_xy) и три компонента тензора напряжений (σ_x, σ_y, τ_xy) не равны нулю, а остальные три компонента тензора напряжения (σ_z, τ_xz τ_yz) и два компонента тензора деформаций (γ_xz, γ_yz) равны нулю. Плоское напряженное состояние типично для тонкостенных конструкций, таких как крылья самолетов. При плоском деформированном состоянии, характернмо для толстых образцов, три компонента тензора деформаций (ε_x, ε_y, γ_xy) и четыре компонента тензора напряжений (σ_x, σ_y,σ_z, τ_xy) не равны нулю, а остальные два компонента тензора напряжения( τ_xz τ_yz) и три компонента тензора деформаций (ε_x,γ_xz,γ_yz) равны нулю):

Для бесконеч­ной пластины из однородного и изотропного линейно-упругого мате­риала единичной толщины с эллипти­ческой центральной трещиной (см. рис.2.2) Y=2/π. Для других сравнительно простых конфигураций тел при эллиптической трещине геометрический фактор Y и, соответственно, G могут быть рассчитаны аналитическими методами, а при сложной конфигурации требуются численные методы.

Инициирование (начало) роста трещины в однородных и изотропных линейно-упругих ма­териалах происходит, когда трещинодвижущая сила (G) достигнет или превысит предельное (критическое) значение (G_С), равное сопротивле­нию материала росту трещины (R) - работе, затрачиваемой на образование единицы площади поверхности при росте трещины (работе разрушения материала). Величина G_С служит параметром трещиностойкости материала, зависящей только от природы материала, т.е. являющейся материальной константой, и критерием разрушения линейно упругого материала с заданной трещиной является неравенство: (2.8).

В случае линейно-упругих гомогенных и изотропных тел с трещиной при заданном типе нагружения параметр трещиностойкости G_С включает в себя не только энергию, необходимую для преодоления сил сцепления всех атомов и молекул (химических и фи­зических связей), действующих в направлении, перпендикулярном плос­кости трещины, т.е. энергию упругого разрыва всех связей в плоскости трещины, равную удвоенной поверхностной энергии материала, но и рассеивание (диссипацию) энергии при образовании единицы площади поверхности по другим механизмам, в первую очередь, затраты энергии на развитие локальных неупругих, например, упруго-пластических деформаций вблизи вершины трещины. Это позволяет применять данный подход ЛУМР к описанию так называемого псевдо-хрупкого роста трещины и соответствующего разрушения материала, при котором вблизи кончика трещины развивается локальная зона неупругих деформаций, размеры которой значительно меньше, чем размеры самой трещины, и сохраняются постоянными в процессе ее роста. При этом для материала в целом допускается сохранение линейной упругости и не накладывает существенных ограничений на расчет трещинодвижущей силы.

Экспериментально параметр трещиностойкости G_С при псевдохрупком разрушении обычно определяют с использованием простых образцов с заданной трещиной, рассчитывая G через податливость образца с трещиной С=Δ/P, где P - сила, действующая вдали от кончика трещины в направлении, перпендикулярном ее основной оси х; Δ – глобальное раскрытие трещины в точках приложения силы. 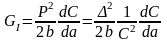(2.9), где b – толщина образца. Для широко используемого образца в виде плоской двухконсольной балки (ДКБ) с полувысотой h, толщиной b и краевой трещиной а (рис.2.3): ; ;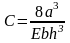 и тогда (2.10).

Рис. Схематическое изображение в виде плоской двухконсольной балки (ДКБ)

Критическое значение G (параметр трещиностойкости G_IС) рассчитывается по экспериментально определенному при монотонном нагружении предельному значению силы P (P_C) по 1-й (левой) части уравнения (2.10) или по предельному глобальному раскрытию трещины (Δ_С) по 2-й (правой) части уравнения (2.10).

Одним из недостатков G-параметра как трещинодвижущей силы является его применимость только к изотропным материалам с самоподобным развитием трещины, так как он не позволяет предсказать направление инициирования и роста трещины при анизотропии сопротивления или когда направление ориентации трещины не совпадает с направлением действия нагрузки. Поэтому был предложен так называемый S-параметр, равный при линейно-упругом поведении материала с трещиной G-параметру и позволяющий не только определять условия начала критического роста трещин, но и предсказывать направление локального деформирования и разрушения материала вблизи вершины трещины, а, соответственно, и направление ее инициирования и роста. Это делает S-параметр особенно привлекательными для оценки условий роста трещин в анизотропных и гетерогенных материалах, к которым относятся полимерные композиционные материалы и в которых направление распростра­нения трещин, как правило, не известно заранее.

Введение S-параметра трещинодвижущих сил базируется на концепции плотности энергии деформации. В теории упругости под плотностью энергии деформации понимают удельную величину, характеризующую энергию деформации материала в единице объема как сумму энергий дилатации (упругого изменения объема) и дисторсии (упругого из­менения формы) единицы объема. Анализ энергетического поля вблизи вершины трещи­ны показал, что его локальная плотность максимальна на границе кончика трещины и убывает пропорционально радиальному расстоянию от ее вершины. Коэффициент пропорциональности S назы­вают коэффициентом плотности энергии деформации. Он характеризует плотность энергии деформации на некотором радиальном расстоянии r от вершины трещины с полярным углом θ относительно ориентации трещины и является мерой интенсивности локально­го поля плотности энергии деформации вблизи вершины трещины, характеризуя трещинодвижущую силу. При этом постулируется, что инициирование и рост трещи­ны происходит в направлении, вдоль которого плотность энергии де­формации минимальна (θ=θ₀), и когда соответствующий этому направлению коэффициент плотности энергии деформации S_min достигнет критического значения Sc. Анали­тически S-критерий роста трещин записывают следующим образом: 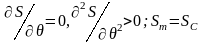при θ=θ₀ . Критическое значение коэффициента плотности энергии деформации Sc рассмат­ривается при этом как материальная константа, характеризующая трещиностойкость материала и по величине обычно равная G_С.