18. Типовые законы распределения дискретной случайной величины.

Дискретная СВ Х имеет геометрическое распределение, если она

принимает значения 0, 1, … , ∞ с вероятностями гдеp – параметр распределения (0 ≤ p ≤ 1), q = 1 – p.

Числовые характеристики геометрического распределения:

Дискретная СВ X имеет биномиальное распределение, если она принимает

значения 0, 1, … , n со следующими вероятностями:

где n, p – параметры распределения (0 ≤ p ≤1), q=1 – p.

Числовые характеристики биномиального распределения:

Дискретная СВ Х имеет распределение Пуассона, если она принимает

значения 0, 1, … , ∞ со следующими вероятностями:

где a – параметр распределения (a > 0).

Числовые характеристики пуассоновской СВ:

19. Типовые законы распределения непрерывной случайной величины. Равномерное, экспоненциальное распределения.

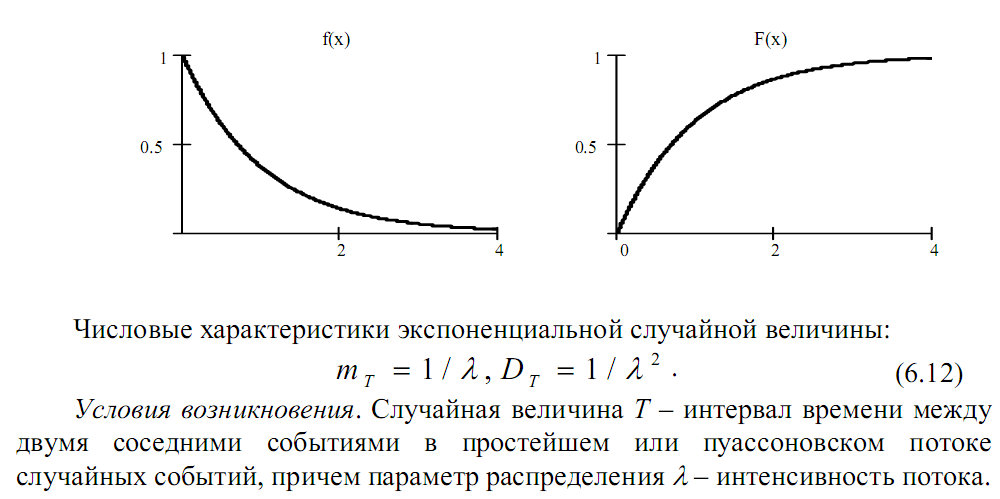
19. Закон распределения функции случайного аргумента.

21.Числовые характеристики функции случайного аргумента

Пусть,где X – случайная величина с известным законом

распределения, и необходимо определить числовые характеристики Y. В том случае, когда закон распределения Y определен , то числовые характеристики Y легко вычислить . Однако, если закон распределения величины Y в явном виде не нужен, а необходимы только ее числовые характеристики, применимы следующие формулы.

Если Х – дискретная случайная величина с известным рядом распределения вероятностей, то

Если Х – непрерывная случайная величина с известной плотностью вероятностей f(x), то формулы принимают вид

22. Двумерные случайные величины. Двумерная функция распределения, ее свойства.

Двухмерная случайная величина (Х, Y) – совокупность двух одномерных случайных величин, которые принимают значения в результате проведения одного и того же опыта. Двухмерные случайные величины характеризуются множествами значений Ωx, Ωy своих компонент и совместным (двухмерным) законом

распределения. В зависимости от типа компонент X, Y различают дискретные, непрерывные и смешанные двухмерные случайные величины. Двухмерную случайную величину (Х, Y) геометрически можно

представить как случайную точку (Х, У) на плоскости х0у либо как случайный

вектор, направленный из начала координат в точку (Х, У).

Двухмерная функция распределения двухмерной случайной величины (Х, Y) равна вероятности совместного выполнения двух событий {Х < х} и {Y < у}:

Геометрически двухмерная функция распределения F(,)xy – это вероятность попадания случайной точки (Х, Y) в бесконечный квадрант с вершиной в точке (х, у), лежащей левее и ниже ее. y (x, y)

Компонента Х приняла значения, меньшие действительного числа х, это функция распределения Fx(X), а компонента Y – меньшие действительного числа у, это функция распределения Fy(Y).

Свойства двухмерной функции распределения:

1. 

2. 

3. 

4. Переход к одномерным характеристикам:

5. Вероятность попадания в прямоугольную область:

Функция распределения - наиболее универсальная форма закона распределения и может быть использована для описания как непрерывных, так и дискретных двухмерных случайных величин.

22. Распределение дискретной двумерной случайной величины (матрица распределения, eё свойства).

Двухмерная случайная величина (Х, Y) является дискретной, если множества значений ее компонент Ωx и Ωy представляют собой счетные множества. Для описания вероятностных характеристик таких величин используется двухмерная функция распределения и матрица распределения.

Матрица распределения представляет собой прямоугольную таблицу, которая содержит значения компоненты X - Ωx = {x1, x2, ..., xn}, значения

компоненты Y - Ωy = {y1, y2, …, ym} и вероятности всевозможных пар значений

pij = p(X = Xi, Y = Yj ), i = 1, …, n, j = 1, …, m.

Свойства матрицы распределения вероятностей:

1. 

2. Переход к ряду распределения вероятностей составляющей X:

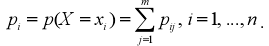
3. Переход к ряду распределения вероятностей составляющей Y:

22. Плотность распределения двумерных случайных величин и ее свойства.

1. Двухмерная случайная величина (X, Y) является непрерывной, если ее функция распределения F(х, у) представляет собой непрерывную, дифференцируемую функцию по каждому из аргументов и существует вторая смешанная производная .

2. Двухмерная плотность распределения f(х, у) характеризует плотность вероятности в окрестности точки с координатами (х, у) и равна второй смешанной производной функция распределения:

3. 

4. Геометрически f(х, у) – это некоторая поверхность распределения, она аналогична кривой распределения для одномерной случайной величины. Аналогично можно ввести понятие элемента вероятности: f(x,y)dxdy . Вероятность попадания значения двухмерной случайной величины (X, Y) в произвольную область D равна сумме всех элементов вероятности для этой области:

5. Свойства двухмерной плотности:

6. 1. f(x, y) ≥ 0.

7. 2. Условие нормировки:

8. Геометрически – объем тела, ограниченный поверхностью распределения и плоскостью x0y, равен единице.

9. 3. Переход к функции распределения:

10. 4. Переход к одномерным характеристикам:

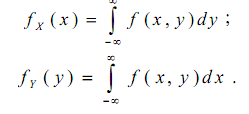
22. Зависимые и независимые случайные величины. Условные законы распределения.

Величина Х независима от величины У, если ее закон распределения не зависит от того, какое значение приняла величина У. Для независимых величин выполняется следующие соотношения, т. е. критерии независимости:

1. F(x, y) = p(X < x, Y < y) = p(X < x)p(Y < y) = FX(x)FY(y) ∀ x, y;

2) для непрерывных – f(x, y) = fX(x)fY(y) ∀ x, y;

3) для дискретных – pij = pi pj , для ∀ i, j.

В том случае, если критерии не выполняются хотя бы в одной точке, величины X и Y являются зависимыми. Для независимых величин двухмерные формы закона распределения не содержат никакой дополнительной информации, кроме той, которая содержится в двух одномерных законах. Таким образом, в случае зависимости величин X и Y переход от двух одномерных законов к двухмерному закону осуществить невозможно. Для этого необходимо знать условные законы распределения.

Условным законом распределения называется распределение одной случайной величины, найденное при условии, что другая случайная величина приняла определенное значение.

Условные ряды распределения для дискретных составляющих Х и Y определяются по формулам:

Матрица распределения вероятностей дискретной двухмерной случайной величины (Х,Y), если ее компоненты зависимы, «порождает» два одномерных ряда вероятностей и два семейства условных рядов вероятностей.

Условные плотности распределения для непрерывных составляющих X и Y определяются по формулам:

Условные законы распределения обладают всеми свойствами соответствующих им одномерных форм законов распределения. Если величины Х и Y независимы, то условные законы распределения равны соответствующим безусловным:

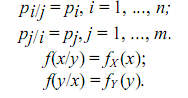
Следует различать функциональную и статистическую (вероятностную) зависимости между случайными величинами. Если Х и Y – случайные величины, которые связаны между собой функциональной зависимостью у = = ϕ (х), то, зная значение Х, можно точно вычислить соответствующие значение Y, и наоборот.

Если между случайными величинами существует статистическая зависимость (величины Х и Y зависимы), то по значению одной из них можно установить только условное распределение вероятностей другой, т.е. определить, с какой вероятностью появится то или иное значение другой величины.

22. Числовые характеристики двумерных величин.

Смешанный начальный момент порядка k + s равен математическому ожиданию произведения Xk и Ys:

Смешанный центральный момент порядка k + s равен математическому ожиданию произведения центрированных величин X k ° и sY °:

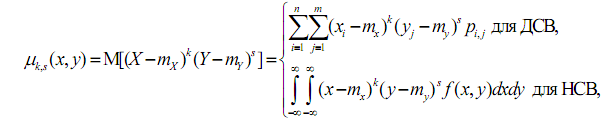
где pij – элементы матрицы распределения вероятностей дискретной случайной величины (ДСВ) (X, Y);

f(x, y) – совместная плотность вероятности непрерывной случайной

величины (НСВ) (X, Y).

Корреляционный момент KXY характеризует степень тесноты линейной зависимости величин X и Y и рассеивание их значений относительно точки (mX, mY):

Коэффициент корреляции XY R характеризует степень линейной зависимости величин и равен:

22. Закон распределения функций двух случайных величин. Числовые характеристики функций двух случайных величин. Композиция законов распределения.