2. Методики розрахунку лінійних електричних ланцюгів

2.1. Пояснення до виконання першого завдання

Для того, щоб знайти струми в розгалуженнях розрахункового електричного кола подібного (рис. 1.1) треба зробити еквівалентні перетворення схем з’єднання споживачів (резисторів). В цій схем змішане з’єднання резисторів представляє собою комбінацію послідовних та паралельних з’єднань. Першим кроком для розв’язання цієї задачі це знаходження еквівалентного опору кола.

Еквівалентний опір (R_екв) знаходиться шляхом спрощення схеми, так щоб отримати один опір. При еквівалентному перетворенні напруга і струм на затискачах схеми не змінюються. Ділянку схеми між точками “в, с” з послідовно-паралельним з’єднанням резисторів R₅…R₇ замінюємо еквівалентною схемою:

R_5…7 = R₆+R₇||R₅.

Замінюємо схему між точками “а, с” з послідовно-паралельним з’єднанням резисторів R_5…7, R₄ і R₃ еквівалентною схемою:

R_3…7 = R₃||R₄+R_5…7.

Еквівалентний (загальний) опір розрахункової схеми буде дорівнювати:

(1.5)

За допомогою формули (1.1) знаходимо струми І₁ та І₂:

(1.6)

Для визначення струму І₃ треба знайти напругу на ділянці “а, с” (U_ас):

(1.7)

тоді струм І₃ буде визначатись як:

(1.8)

Струм І₄ визначаємо за допомогою першого закону Кірхгофа:

(1.9)

Для визначення струмів І₅, І₆ треба знайти напругу на ділянці “в, с” (U_вс):

(1.10)

В цьому разі:

(1.11)

Активну потужність кола визначається за формулою:

Р= І₁²·R _екв. (1.12)

2.2. Пояснення до виконання другого завдання

За другим законом Кірхгофа значення напруги:

(2.1)

Припустимо, що струм у колі

Підставимо значення струму в рівняння (2.1) і отримуємо:

(2.2)

де

Векторна діаграма напруг і струмів на окремих ділянках схеми відповідно до одержаного рівняння для випадку X_L X_C (рис.2.1).

Р ис.2.1. Векторна діаграма струмів та напруг

Як видно з векторної діаграми, у випадку, коли X_L>X_C напруга випереджає струм на кут j, тому миттєве значення напруги становить:

. (2.3)

Виділимо трикутник максимальних значень напруг (рис.2.2), зменшимо сторони трикутника в разів і одержимо трикутник діючих значень напруг. Сторони трикутника можна знайти за формулами

(2.4)

де R, X_L, X_C, Z– відносно активний, індуктивний, ємкісний і повний опір кола.

Якщо сторони трикутника напруг розділити на величину струму, то одержимо трикутник опорів (рис. 2.2 )

Р ис.2.2. Трикутник опорів

Із трикутників опорів знаходимо повний опір кола синусоїдного струму та кут зсуву фаз:

(2.5)

(2.6)

Закон Ома для діючих значень напруги і струму:

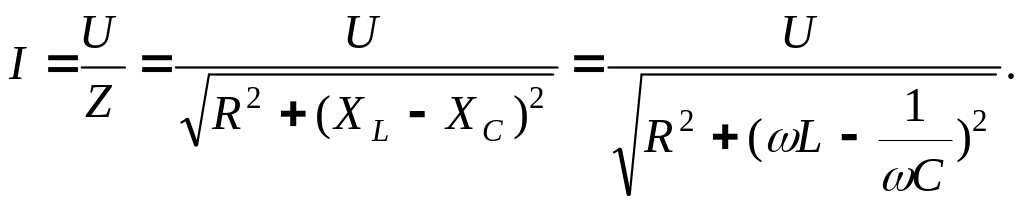(2.7)

Помножимо сторони трикутників опорів на величину квадрату струму і одержимо трикутник потужностей (рис 2 4).

Р ис. 2.3. Трикутник потужностей

Сторони трикутника знаходимо за формулами:

(2.8)

де Р – активна потужність (Вт), Q_L, Q_C – реактивна потужність (Вар) і S – повна потужність кола (ВА).

Коефіцієнт потужності:

(2.9)