3. Порядок виконання роботи

Параметри ланки для виконання роботи задаються викладачем. Після запуску Mathcad треба:

ввести параметри ланки;

задати інтервал зміни частоти в межах 0 – 1000 1/с та кроком 2 1/с;

виконати розрахунок дійсної та уявної частини годографа Михайлова та ;

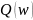побудувати годограф Михайлова на комплексній площині при зміні частоти 𝜔 від 0 до ∞;

зробити висновок щодо стійкості системи;

дослідити вплив коефіцієнта підсилення САР на годограф Михайлова.

4. Зміст звіту

4. 1. Схема і математична модель ланки 4.

4. 2. Таблиця 1 результатів розрахунку функцій ланки.

4. 3. Годограф Михайлова.

5. Запитання для контролю

5.1. Яке призначення критерію стійкості Михайлова?

5.2. Якими є умови стійкості замкнутої САР?

5.3. Вплив зміни коефіцієнта підсилення САР на її стійкість.

Лабораторна робота №5. Побудова динамічних характеристик ланок розімкнутої САР

Мета роботи. Побудова частотних та логарифмічних характеристик ланок розімкнутої системи

1. Математична модель системи

Структурна схема САР приведена на рис.1. Розімкнуту САР одержуємо при розмиканні кола зворотного зв’язку на вході суматора.

Рис.1. Структурна схема САР

Передавальні функції ланок такі:

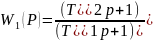(1)

(2)

(3)

Передавальна функція розімкнутої САР згідно з теоремою 1 (послідовне з’єднання ланок): (4)

де – загальний коефіцієнт підсилення розімкнутої САР.

Записуємо комплексну передавальну функцію (КПФ):

(5)

Записуємо вираз модуля КПФ згідно з правилом, по якому модуль добутку комплексних чисел дорівнює добутку їх модулів, а аргумент – сумі співмножників.

Модуль: ; (6)

Аргумент: . (7)

Для виявлення характеру АФЧХ визначаємо дійсну частину КПФ – та уявну частину КПФ – при зміні частоти в межах від 0 до ∞. Побудувавши графік в системі координат 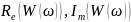одержимо годограф АФЧХ.

Логарифмічну амплітудно-частотну характеристику (ЛАЧХ) САР знаходимо з виразу: . (8)

сполучні частоти САР знаходять як:

(9)

Побудову ЛАЧХ виконують дотримуючись такої методики:

1) відкладають уздовж осі частот сполучні частоти ;

2) на частоті відкладають ординату, яка дорівнює (точка А, рис. 2);

3) через точку А проводять пряму з нахилом 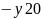децибел на декаду(де – порядок астатизму системи, для нашого випадку , цей відрізок буде низькочастотною асимптотою ЛАЧХ системи);

4) якщо перша частота сполучення , то через точку А пройде продовження низькочастотної асимптоти;

5) після кожної із частот сполучення 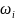необхідно змінювати нахил ЛАЧХ на 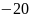децибел на декаду, якщо ця частота визначається постійною часу

Рис. 2. До визначення частоти

співмножника 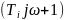знаменника передавальної функції, і на децибел на декаду, якщо сполучна частота визначається постійною часу співмножника чисельника.

Система має астатизм першого порядку ( ), тому низькочастотна асимптота і її продовження визначається з виразу:

. (10)

У точці перетину асимптоти чи її продовження з віссю частот маємо , звідки . Використовуючи цю властивість можна по ЛАЧХ визначити коефіцієнт підсилення САР .
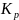