2. Зміст роботи

2.1. Розрахунок динамічних характеристик ланки другого порядку за допомогою Mathcad.

2.2. Побудова графіків динамічних характеристик ланки другого порядку.

3. Запис математичної моделі ланки другого порядку

Прикладом ланки другого порядку може бути електричне коло з елементами R, L, C, схема якого приведена на рис. 1.

Рис.1. Принципова та функціональна схеми ланки другого порядку

Вхідною величиною ланки є напруга U_вх , вихідною – напруга на конденсаторі U_с . Диференційне рівняння ланки, яке встановлює зв’язок між вхідною, вихідною координатою та параметрами ланки можна одержати:

згідно з другим законом Кірхгофа:

U_вх= U_L +U_R + U_с . (18)

Напруга на резисторі R згідно з законом Ома:

U_R =iR , (19)

де і - струм в електричному колі ланки.

Струм в колі конденсатора . (20)

При послідовному з’єднанні струми в елементах кола одинакові: .

Напруга на індуктивності: U_L = (21)

Із рівняння (20) знаходимо похідну від струму в колі:

= . (22)

Підставимо в рівняння (18) значення доданків згідно з їхніми значеннями (20, 21, 22), одержимо: + . (23)

Приведемо рівняння до загального вигляду

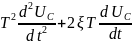+ , (24)

де − постійна часу ланки, с;

– характеристика гальмування перехідного процесу;

=1 – коефіцієнт підсилення ланки.

Відносний коефіцієнт згасання: 𝜉= .

Запишемо диференційне рівняння в вигляді перетворення по Лапласу при нульових початкових умовах , одержуємо:

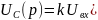+1) ) , (25)

де р – оператор Лапласа.

Передавальна функція ланки має такий вигляд:

W(p)= (26)

Характеристичне рівняння: +1= 0 згідно з (7) має два корені ,

за допомогою яких знаходимо постійні часу: ; двох

послідовно з’єднаних аперіодичних ланок.

Характеристичне рівняння у цьому випадку має вигляд: . Параметри варіантів ланки для виконання лабораторної роботи приведені в табл. 1.1.

Параметри ланки Талиця 1.1.

Параметри ланки	Робочі місця
	1	2	3	4	5	6	7	8
R, ом	23	33	38	45	50	55	65	75
L, мГн	100	200	300	400	500	600	800	1000
С, мКф	0,8	0,9	1,1	1,3	1,6	1,8	2,0	2,2