
- •Теоретичні поняття
- •Зв'язки
- •Кон’юнкція.
- •Диз’юнкція. Диз’юнкцією (логічним додаванням) висловлювань і називається висловлювання , яке істинно тоді і тільки тоді, коли істинно або висловлювання , або висловлювання , або обидва.
- •Інверсія.
- •Еквівалентність.
- •Еквівалентні висловлювання
- •Основні еквівалентності
- •Для кон'юнкції
- •Для диз'юнкції
- •Загальні еквівалентності.
- •Заперечення кон’юнкції є диз’юнкція заперечень ;
- •Методи доведення
- •Метод математичної індукції
- •Квантори
- •Зв’язок між кванторами Розглянемо правила переходу від одних формул до рівносильних їм.
- •Перестановка однойменних кванторів
- •Перенесення квантора через заперечення
- •Винос квантора за дужки
- •Завдання № 1.
- •Завдання № 2.
- •Завдання № 3
- •Завдання № 4
Завдання № 2.
Побудуйте таблиці істинності для висловлювань:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Побудуйте таблиці істинності для висловлювань
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Завдання № 3
Варіант № .
Довести, що при будь-якому натуральному n число ділиться на 3.
Довести, що при будь-якому натуральному n справедлива рівність
 .
.
Варіант № .
Довести, що при будь-якому натуральному n число
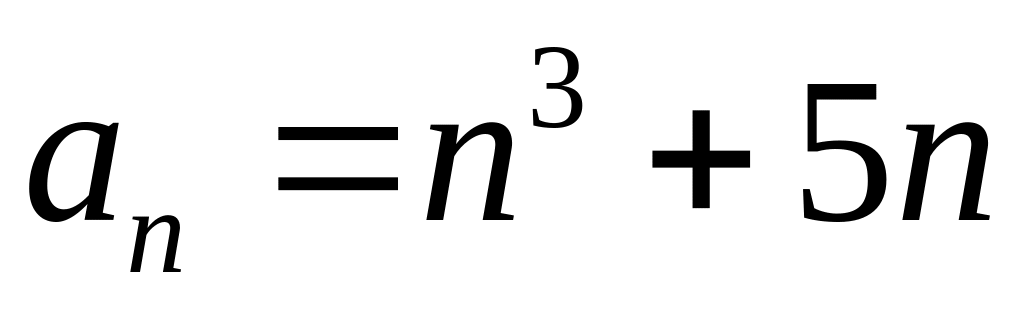 ділиться на 6.
ділиться на 6.Довести, що при будь-якому натуральному n справедлива рівність
 .
.
Варіант № .
Довести, що при будь-якому натуральному n число
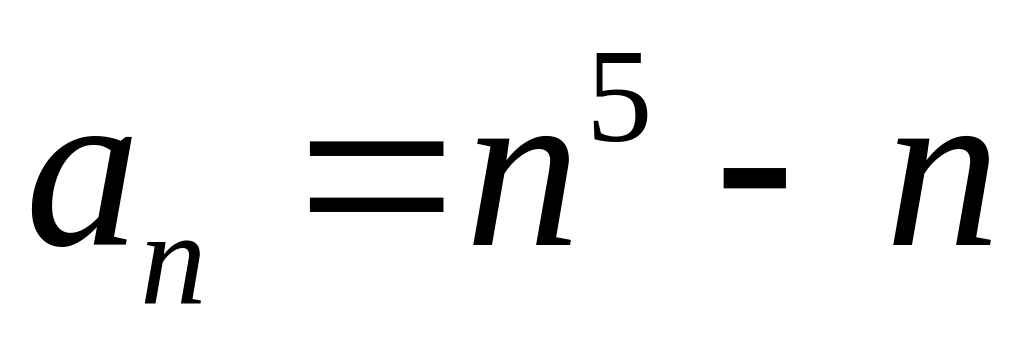 ділиться на 30.
ділиться на 30.Довести, що при будь-якому натуральному n справедлива рівність
 .
.
Варіант № .
Довести, що при будь-якому натуральному n число
 ділиться на 17.
ділиться на 17.Довести, що для будь-якого натурального
 має місце нерівність
має місце нерівність
 ,
де
,
де
 .
.
Варіант № .
Довести, що при будь-якому натуральному n число
 ділиться на 133.
ділиться на 133.Довести, що при будь-якому натуральному n
 .
.
Варіант № .
Довести, що при будь-якому натуральному n число
 ділиться на 33.
ділиться на 33.Довести, що при
 вірно
вірно
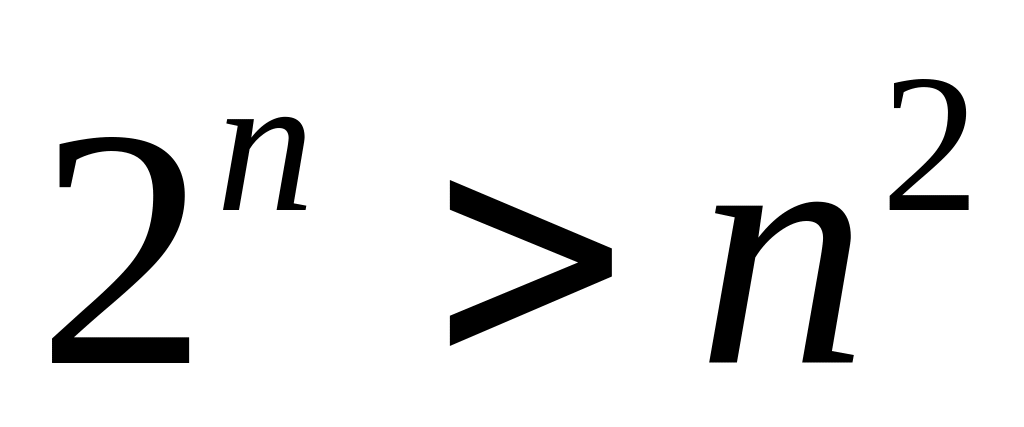 .
.
Варіант № .
Довести, що при будь-якому натуральному n число
 ділиться на 17.
ділиться на 17.Довести, що при будь-якому натуральному n справедлива нерівність
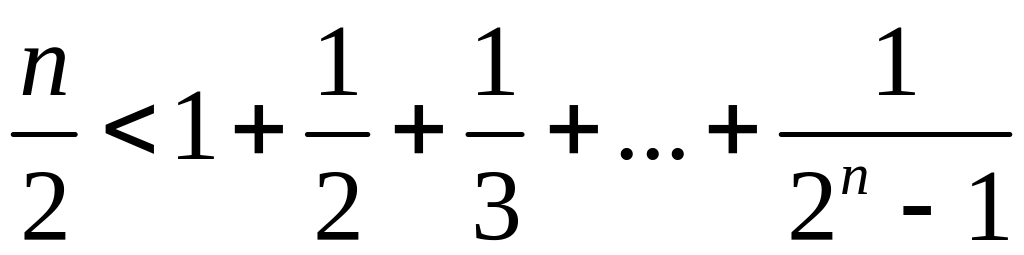 .
.
Варіант № .
Довести, що при будь-якому натуральному n число
 ділиться на 11.
ділиться на 11.Довести, що при будь-якому натуральному n справедлива рівність
 .
.
Варіант № .
Довести, що при будь-якому натуральному n число
 ділиться на 19.
ділиться на 19.Довести, що при будь-якому натуральному n справедлива рівність
 .
.
Варіант № .
Довести, що при будь-якому натуральному n число
 ділиться на 19.
ділиться на 19.Довести, що при будь-якому натуральному n справедлива рівність
 .
.
Варіант № .
Довести, що при будь-якому натуральному n число
 ділиться на 59.
ділиться на 59.Довести, що при будь-якому натуральному n справедлива рівність

Варіант № .
Довести, що при будь-якому натуральному n число
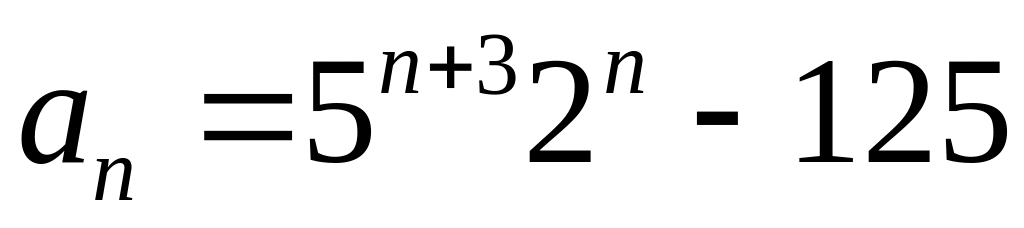 ділиться на 45.
ділиться на 45.Довести, що при будь-якому натуральному n справедлива рівність
 .
.
Варіант № .
Довести, що при будь-якому натуральному n число
 ділиться на 6.
ділиться на 6.Довести, що при будь-якому натуральному n справедлива рівність
 .
.
Варіант № .
Довести, що при будь-якому натуральному n число
 ділиться на 30.
ділиться на 30.Довести, що при будь-якому натуральному n справедлива рівність
 .
.
Варіант № .
Довести, що при будь-якому натуральному n число
 ділиться на 148.
ділиться на 148.Довести, що при будь-якому натуральному n справедлива рівність
 .
.
Варіант № .
Довести, що при будь-якому натуральному n число
 ділиться на 27.
ділиться на 27.Довести, що при будь-якому натуральному n справедлива рівність
 .
.
Варіант № .
Довести, що при будь-якому натуральному n число
 ділиться на 48.
ділиться на 48.Довести, що при будь-якому натуральному n справедлива рівність
 .
.
Варіант № .
Довести, що при будь-якому натуральному n число
 ділиться на 9.
ділиться на 9.Довести, що при будь-якому натуральному n справедлива рівність
 .
.
Варіант № .
Довести, що при будь-якому натуральному n число
 ділиться на 6.
ділиться на 6.Довести, що при будь-якому натуральному n справедлива рівність
 .
.
Варіант № .
Довести, що при будь-якому натуральному n число
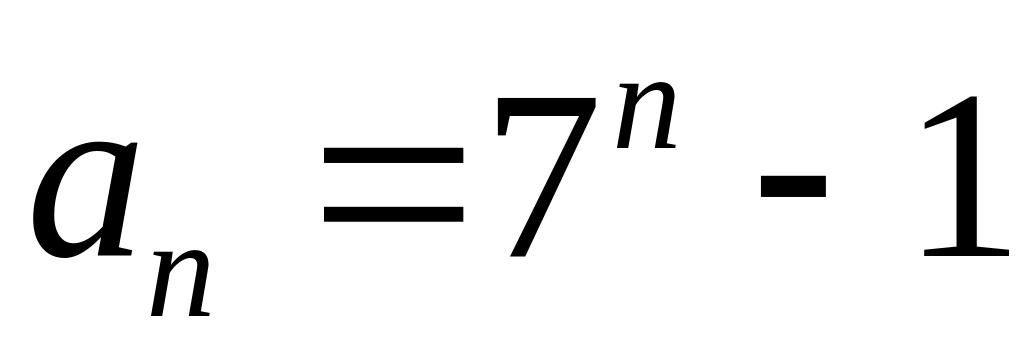 ділиться на 6.
ділиться на 6.Довести, що при будь-якому натуральному n справедлива рівність
 .
.
