Квантори

Перед тим, як ввести поняття квантора розглянемо поняття множини. Більш докладно про множини мова піде у другій частині, а поки що зазначимо, що множина це невизначуване поняття. Можна говорити, що множина – це сукупність об’єктів, які мисляться як єдине ціле. Множини позначаються великими латинськими літерами, а об’єкти, що до них входять – маленькими латинськими літерами.

Наприклад, зі шкільного курсу алгебри добре відома множина цілих чисел  , множина дійсних чисел  . Можна розглянути також множину, що складається з чотирьох елементів 5; тролейбус №2; факультет АТЗ; людина}. Множину, що задовольняє деякому обмеженню: нехай це деяка властивість , тоді   це множина тих , що мають властивість .

1. Квантор (символ) загальності . Запис читається так: «для будь-якого », «для всіх х», «для кожного х».

– для всіх х з множини вірна властивість ,

2. Квантор (символ) існування . Запис 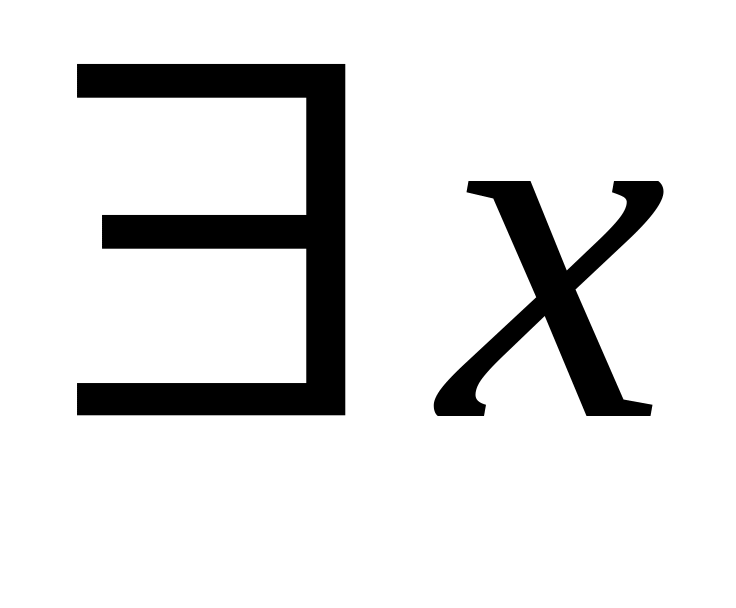означає «існує х», «знайдеться х».

– існує з множини , таке, що виконується властивість , тобто знайдеться хоча б один елемент , для якого – істинне.

3. Квантор існування та єдиності – існує та єдиний

– існує та єдине з множини , що , тобто найдеться один та тільки один елемент , для якого – істинне.

Приклад 13. Запишемо висловлювання “Всі студенти повинні вчитися” мовою логіки.

Розглянемо множину  – студенти, та властивість  – людина повинна вчитися, тоді  – будь-яка людина, що є студентом повинна вчитися.

Приклад 14. Висловлювання “Через будь-які три різні точки простору можна провести єдину площину” запишеться так:

.

Приклад 15. Запишемо висловлювання “Для будь-якого натурального існує дійсний такий, що їх частка дорівнює цілому числу” мовою логіки.

– це висловлення істинне. (Будь-яке натуральне число, принаймні, при діленні само на себе дає цілу частку.)

Зв’язок між кванторами Розглянемо правила переходу від одних формул до рівносильних їм.

1. Перестановка однойменних кванторів

1. 

2. 

1. Перенесення квантора через заперечення

   1. 

   2. 

Приклад 16. Висловлювання “Не всі студенти вчаться” рівносильне висловлюванню “Існує студент, який не вчиться”. Мовою логіки, використовуючи позначення введені в прикладі 13, це висловлювання можна записати так:

.

Приклад 17. Побудувати заперечення для кожного з наступних висловлювань:

• Істинне висловлювання: 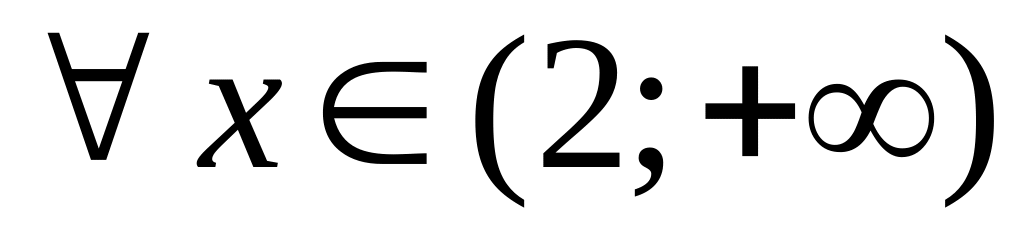: . (Читається так: для будь-якого більшого за двійку, його квадрат більше чотирьох.)

Заперечення: : – хибне висловлювання. (Читається так: існує більший за двійку, такий що його квадрат менше чотирьох)

• Хибне висловлювання: “Деякі люди безсмертні”.

Заперечення: “Всі люди смертні” – істинне висловлювання.

3. Винос квантора за дужки

   1. 

   2. 

   3. 

   4. 

Висловлювання не залежить від .

ЗАВДАННЯ ДЛЯ ПРАКТИЧНИХ ЗАНЯТЬ

1. Які з наступних виразів є висловлюваннями і чому:

   1. ;

   2. Я живу на Україні;

   3. Учні середньої школи вивчають математику;

   4. при ;

   5. ;

   6. ;

   7. .

2. Визначте вид складного висловлювання та запишіть його формулою логіки висловлювань:

1. “Не купуй кота в мішку, якщо тобі не потрібний мішок”.

2. “Прямо – ближче, обдумано – швидше”.

3. “Якщо я маю намір поїхати в село тоді й тільки тоді, коли я здам іспит, то якщо я не здам іспит, то я лишуся в місті”.

3. Сформулюйте заперечення наступних висловлювань у стверджувальній формі, тобто так, щоб вони не починалися зі слів “невірно, що …”:

   1. “Якщо я займаюся в спортивній школі, то я вмію плавати”;

   2. “Якщо Санкт-Петербург розташований на Неві, то білі ведмеді живуть в Африці”;

   3. “Якщо в даному чотирикутнику діагоналі взаємно перпендикулярні, то цей чотирикутник – ромб”.

4. Які з наступних імплікацій істинні та чому:

   1. Якщо , то ;

   2. Якщо , то ;

   3. Якщо , то існують чорти;

   4. Якщо , то ;

5. Серед наданих тверджень знайдіть еквівалентні:

   1. Якщо – сепулька, то – мешканець Інтеропії,

   2. Якщо – не сепулька, то – не мешкає в Інтеропії,

   3. Якщо – мешканець Інтеропії, то – сепулька,

   4. Якщо – сепулька, то – не мешкає в Інтеропії.

6. У наступних реченнях замініть крапки словами: “необхідно та досить”, “необхідно, але не досить”, “досить, але не необхідно” так, щоб вийшло вірне твердження:

   1. Для того щоб виграти в лотереї ... мати хоча б один лотерейний квиток.

   2. Для того щоб із трьох чисел хоча б два були рівні між собою, …, щоб .

   3. Для того щоб медіана трикутника дорівнювала половині сторони, яку вона ділить, ..., щоб трикутник був прямокутним.

7. Складіть таблиці істинності для висловлювань

1. 

2. 

3. 

4. 

5. 

8. На іспиті викладач пропонує студентові п’ять тверджень, щодо яких потрібно відповісти, істинні вони чи хибні. Студент знає, що викладач завжди дає істинних тверджень більше, ніж хибних, і ніколи не задає три питання підряд, що вимагають однакової відповіді. Зі змісту першого й останнього твердження йому ясно, що відповіді на них повинні бути протилежними. Єдине питання, відповідь на яке він знає – друге. Це вже гарантує йому правильні відповіді на всі питання. Що знає студент про друге питання? Якими повинні бути відповіді на всі 5 питань?

9. Задача Р. Смалліана про конгресменів. У деякому конгресі засідають 100 політичних діячів. Кожний з них або продажний, або чесний. Відомі наступні два факти:

1. принаймні, один з конгресменів є чесним;

2. з кожної довільно обраної пари конгресменів, принаймні, один продажний.

Чи можна за допомогою цих двох тверджень визначити, скільки конгресменів у цьому конгресі будуть чесними, а скільки – продажними? (Дві розповсюджені відповіді 50 і 50 або 51 і 49 – не є правильними).

10. Довести, що для будь-яких цілих число парне.

11. Довести, що для будь-яких натуральних n вираз ділиться на 19.

12. Довести, що для будь-яких натуральних справедлива рівність

    1. ;

    2. .

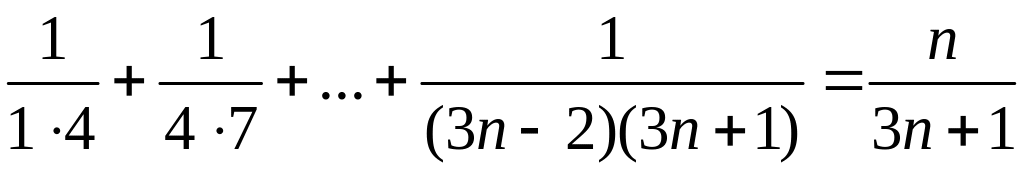13. Довести нерівність Бернуллі: для будь-якого натурального , для кожного виконується нерівність .

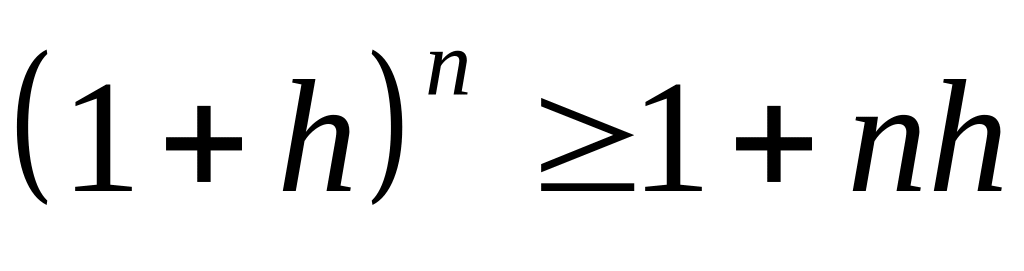14. Запишіть наступні висловлювання з використанням кванторів:

    1. Існує число таке, що .

    2. Будь-яке число або додатне, або від’ємне, або дорівнює нулю.

    3. Усі тигри більш за кішок.

    4. Деякі студенти не прийняли участі у олімпіаді.

15. В наданих висловлюваннях заповніть пропуски необхідними кванторами:

    1. Для двох різних точок … пряма, що проходить через них.

    2. На … прямій … дві різні точки.

    3. Із будь-якого становища … вихід.

ВАРІАНТИ ІНДИВІДУАЛЬНИХ ЗАВДАНЬ