1. Заперечення кон’юнкції є диз’юнкція заперечень ;

2. заперечення диз’юнкції є кон’юнкція заперечень .

Доведемо лише перший з них.

1	1	0	0
0	1	0	0
1	0	0	0
0	0	1	1

Третій та четвертий стовпці співпадають. Закон доведено.

8. Заперечення імплікації 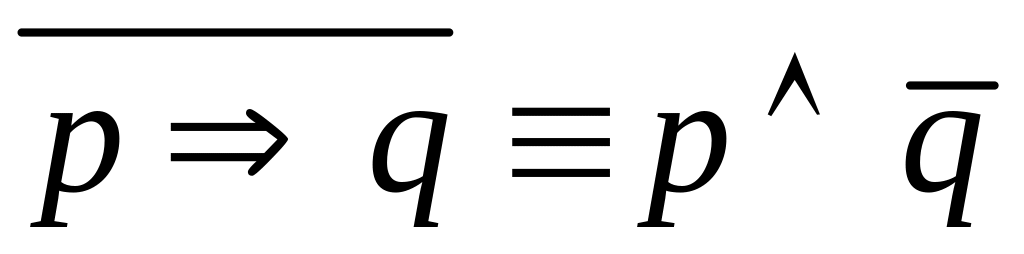(є посилка й відсутній висновок).

Цю формулу можна також довести за допомогою таблиці істинності. Інший спосіб: скористатися для доведення попередніми законами .

9. Заперечення подвійної імплікації .

10. Доведемо цю формулу також за допомогою попередніх законів:

.

Методи доведення

Багато математичних об’єктів можна зробити більш наглядними, якщо користуватись символами і законами логіки. Наприклад, за допомогою логіки були формалізовані і розвинені методи теорії доведень.

Пряме доведення. Правильність розглянутого твердження перевіряється безпосередньо, з використанням визначень або вже доведених тверджень.

Доведення методом “від протилежного”. Розглядається твердження, протилежне тому, що доводиться, та виявляється його невірність або шляхом міркувань, або побудовою контрприклада.

Доведення методом виключення. Істинність доводиться шляхом послідовного доведення хибності всіх складових висловлювання (диз’юнкції), крім одного.

Метод математичної індукції

Метод математичної індукції застосовується для доведення тверджень, які залежать від натурального числа . В основі лежить принцип повної індукції: Якщо будь-яке твердження доведене при (у випадку, якщо при твердження не має сенсу, то перевірку роблять для найменшого значення , при якому воно має сенс) і якщо з припущення, що воно справедливе для натурального , випливає, що воно вірно для наступного натурального числа , тоді це твердження вірно для будь-якого натурального числа.

Перевірка справедливості твердження при називається базою індукції. Доведення твердження при , у припущенні його справедливості при називається індуктивним переходом і позначається .

Приклад 9. Довести, що ділиться на 3.

Розв'язок.

1. Перевіримо базу індукції, тобто , .

= , ділиться на 3.

База індукції вірна.

2. Індуктивний перехід .

Припустимо, що для деякого натурального

ділиться на 3.

Покажемо, що звідси витікає твердження при :

.

ділиться на 3 за індуктивним припущенням, а – має 3 множником, значить, на підставі принципу математичної індукції можна стверджувати, що ділиться на 3 для будь-якого натурального .

Приклад 10. Довести формулу

.

Розв'язок.

1. Перевіримо базу індукції: 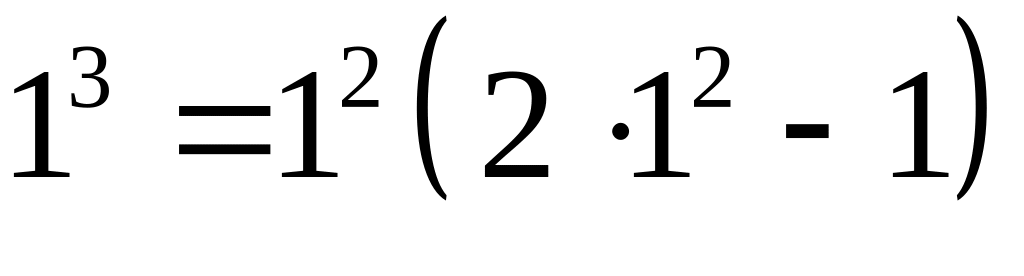, . База індукції вірна.

2. Індуктивний перехід .

Припустимо, що для деякого натурального формула вірна, тобто

.

Покажемо, що звідси витікає аналогічна рівність при :

.

Тепер на підставі принципу математичної індукції можна стверджувати справедливість даної формули для будь-якого натурального .

Приклад 11. Довести формулу:

(2)

де .

Розв’язок.

1. Перевіримо базу індукції: .

.

База індукції вірна.

2. Індуктивний перехід :

Припустимо, що для деякого натурального формула вірна, тобто

.

Тоді для

На підставі принципу математичної індукції можна стверджувати справедливість формули (2) для будь-якого натурального .

Приклад 12. Для будь-яких натуральних довести нерівність

Розв'язок.

1. Перевіримо базу індукції: . База індукції вірна.

2. Індуктивний перехід . Припустимо, що при формула вірна, тобто .

Для

,

оскільки – натуральне.

За допомогою принципу математичної індукції ми довели надану нерівність для будь-якого натурального .