
- •Билет №2.
- •Упростить релейно-контактную схему и записать условие проводимости.
- •Билет №3.
- •Билет №4.
- •Упростить релейно-контактную схему и записать условие проводимости.
- •Билет №5.
- •Упростить релейно-контактную схему и записать условие проводимости.
- •Билет №6.
- •Упростить релейно-контактную схему и записать условие проводимости.
- •На множестве определены отношения а) ,
- •Билет №7.
- •Билет №8.
- •Доказать, что бинарное отношение есть отображение и отображение . Будет ли каждое из этих отображений инъективным, сюръективным, обратимым?
- •Билет №9.
- •Билет №10.
- •Доказать, что бинарное отношение есть отображение и отображение . Будет ли каждое из этих отображений инъективным, сюръективным, обратимым?
- •Билет №11.
- •Упростить формулу a .
- •Упростить релейно-контактную схему и записать условие проводимости.
- •Билет №12.
- •Доказать с помощью таблицы истинности, что (ab) (ac) a (bc).
- •Упростить релейно-контактную схему и записать условие проводимости.
- •Билет №13.
- •Упростить так, чтобы полученное выражение не содержало вхождений букв а, в, с.
- •Доказать с помощью таблицы истинности, что (ab) b a b.
- •Упростить релейно-контактную схему и записать условие проводимости.
- •Билет №14.
- •Билет №15.
- •Билет №16.
- •Билет №17.
- •Билет №18.
- •Билет №19.
- •Билет №20.
- •Билет №21.
- •Билет №22.
- •Будет ли формула (a(bc)) ((ab) (ac)) тождественно истинной?
- •Билет №23.
- •Билет №24.
- •Доказать с помощью таблицы истинности, что (ab) (ac) a (bc).
- •Упростить релейно-контактную схему и записать условие проводимости.
- •На множестве определены отношения а) ,
- •Билет №25.
- •Билет №26.
- •Билет №27.
- •Доказать, что формула в является логическим следствием формул .
- •Билет №28.
- •Билет №29.
- •Билет №30.
- •Доказать, что отношение есть отображение и отображение . Будет ли каждое из этих отображений инъективным, сюръективным, обратимым?
- •Билет №31.
- •Доказать с помощью таблицы истинности, что (ab) (ac) a (bc).
- •Упростить релейно-контактную схему и записать условие проводимости.
- •Билет №32.
- •Доказать с помощью таблицы истинности, что (ab) b a b.
- •Билет №33.
- •Упростить так, чтобы полученное выражение не содержало вхождений букв а, в, с.
- •Доказать от противного, что формула является логическим следствием формул
Билет №8.
Упростить
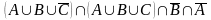 так, чтобы полученное выражение не
содержало букв А, В, С.
так, чтобы полученное выражение не
содержало букв А, В, С.С помощью таблицы истинности установить, будет ли формула
 тождественно
истинной.
тождественно
истинной.Пусть А - множество различных букв в слове «УНИВЕРСИТЕТ», В - множество букв в слове «АКАДЕМИЯ». Задать множества A, B,AB, AB, A\B, B\A перечислением элементов.
Упростить релейно-контактную схему и записать условия проводимости.
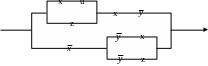
Доказать, что
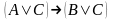 является логическим следствием формулы
является логическим следствием формулы

Пусть
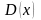 – длина диагонали прямоугольника х.
На множестве прямоугольников определены
отношения: а)
– длина диагонали прямоугольника х.
На множестве прямоугольников определены
отношения: а)
 ,
,
б)
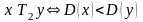 ,
,
в)
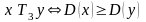 .
.
Какие из этих отношений являются эквивалентностью или порядком? В первом случае охарактеризовать классы эквивалентности, во втором – определить тип порядка.
Доказать, что бинарное отношение есть отображение и отображение . Будет ли каждое из этих отображений инъективным, сюръективным, обратимым?
У одного человека есть 7 разных книг, а у другого – 9 книг. Сколькими способами они могут обменять друг с другом по две книги?
Билет №9.
Доказать, что
 .
.С помощью таблицы истинности проверить равносильности:
 .
.Пусть А – множество целых решений неравенства
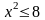 ,
В – множество натуральных решений
неравенства
,
В – множество натуральных решений
неравенства
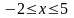 .
Задать перечислением элементов множества
A,
B,AB,
AB,
A\B,
B\A.
.
Задать перечислением элементов множества
A,
B,AB,
AB,
A\B,
B\A.Упростить релейно-контактную схему и записать условия проводимости.
Является ли формула
 логическим следствием формулы
логическим следствием формулы
 ?
?На множестве всех городов мира определены отношения:
а) «число жителей х равно числу жителей у»,
б) «число жителей х больше числа жителей у»,
в) «число жителей х меньше числа жителей у».
Какие из этих отношений являются эквивалентностью или порядком? В первом случае охарактеризовать классы эквивалентности, во втором – определить тип порядка.
Доказать, что отношение «у – остаток от деления х на 8» есть отображение и отображение
 ,
где
,
где
 .
Будет ли каждое из этих отображений
инъективным, сюръективным, обратимым?
.
Будет ли каждое из этих отображений
инъективным, сюръективным, обратимым?Сколько различных команд по 8 человек можно составить из 11 человек так, чтобы данные два человека не попали в одну и ту же команду?
Билет №10.
Доказать и проиллюстрировать диаграммой Венна, что:

Доказать с помощью таблицы истинности, что
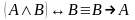 .
.Пусть U={x (xN)(1 x 20)}, A={x (xU)( x5)}, B={x (xU)( x3)}. Задать множества A, B,AB, AB, A\B, перечислением элементов.
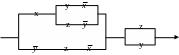
Упростить релейно-контактную схему и записать условия проводимости.
Доказать, что
 есть логическое следствие
есть логическое следствие
Пусть
 – высота треугольника х.
На множестве всех треугольников
определены отношения: а)
– высота треугольника х.
На множестве всех треугольников
определены отношения: а)
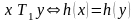 ,
,
б)
 ,
,
в)
 .
.
Какие из этих отношений являются эквивалентностью или порядком? В первом случае охарактеризовать классы эквивалентности, во втором – определить тип порядка.
