Билет №1.

1. Доказать и проиллюстрировать диаграммой Венна, что (A\B)\C  (A\B)\(B\C)

2. Будет ли формула (A(BC))  ((AB)  (AC)) тождественно истинной?

3. Пусть A={x (xN)(12x)}, B={x (xN)(18x)}. Задать множества A, B,AB, AB, A\B, B\A перечислением элементов.

4. Упростить релейно-контактную схему и записать условие проводимости.

5. Доказать от противного, что формула 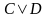является логическим следствием формул

6. На множестве жителей многоэтажного дома определены отношения:

а) «х живет на одном этаже с у»,

б) «х живет выше у»,

в) «х живет не выше у».

Какие из этих отношений являются эквивалентностью или порядком? В первом случае охарактеризовать классы эквивалентности, во втором – определить тип порядка.

7. Доказать, что отношение есть отображение и отображение . Будет ли каждое из этих отображений инъективным, сюръективным, обратимым?

8. Сколькими способами можно выбрать из 15 человек группу людей для работы, если в группу может входить 2, 4, 6, 8, 10 или 12 человек ?

Билет №2.

1. Доказать и проиллюстрировать диаграммой Венна, что (AC)\(BC)  (A\B)C

2. Упростить формулу A .

3. Пусть U={x (xN)(1 x 20)}, A={x (xU)( x5)}B={x (xU)( x3)}. Задать множества A, B,AB, AB, A\B, перечислением элементов.

4. Упростить релейно-контактную схему и записать условие проводимости.

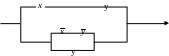
5. Доказать, что не является логическим следствием .

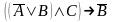6. На множестве определены отношения а) ,

б) ,

в) .

Какие из этих отношений являются эквивалентностью или порядком? В первом случае охарактеризовать классы эквивалентности, во втором – определить тип порядка.

7. Доказать, что бинарное отношение «у – периметр прямоугольника х» есть отображение и отображение , где , А – множество всех прямоугольников. Будет ли каждое из этих отображений инъективным, сюръективным, обратимым?

8. Сколькими способами можно сложить 8 различных книг в две сумки (порядок книг не имеет значения, а порядок сумок важен).

Билет №3.

1. Упростить 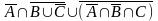так, чтобы полученное выражение не содержало вхождений букв А, В, С.

2. Доказать с помощью таблицы истинности, что (AB) (AC)  A (BC).

3. Пусть A – множество различных букв, входящих в Вашу фамилию, В – множество всех гласных букв в алфавите. Задать множества A, B,AB, AB, A\B, B\A перечислением элементов.

4. Упростить релейно-контактную схему и записать условие проводимости.

5. Доказать, что формула В является логическим следствием формул .

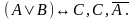6. Пусть 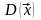– длина вектора . На множестве векторов V определены отношения:

а) ,

б) ,

в) .

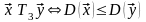Какие из этих отношений являются эквивалентностью или порядком? В первом случае охарактеризовать классы эквивалентности, во втором – определить тип порядка.

7. Доказать, что бинарное отношение есть отображение и отображение . Будет ли каждое из этих отображений инъективным, сюръективным, обратимым?

8. Сколькими существует девятизначных чисел, у которых все цифры различны?

Билет №4.

1. Доказать и проиллюстрировать диаграммой Венна, что (AB)\(AB) = A  (B )

2. Доказать с помощью таблицы истинности, что (AB) B  A B.

3. Пусть U-множество всех четырехугольников плоскости, Р–множество прямоугольников, R – множество всех ромбов, Т – множество всех трапеций. Задать множества PR, P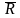 , RT, указанием характеристического свойства.

4. Упростить релейно-контактную схему и записать условие проводимости.

5. Доказать, что формула является логическим следствием формул (от противного).

6. На множестве комплексных чисел определены отношения

а) ,

б) ,

в) .

Какие из этих отношений являются эквивалентностью или порядком? В первом случае охарактеризовать классы эквивалентности, во втором – определить тип порядка.

7. Доказать, что отношение «у – первая цифра в записи числа х» есть отображение 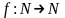и отображение , где .. Будет ли каждое из этих отображений инъективным, сюръективным, обратимым?

8. Сколько можно составить четырехзначных чисел из 5 разных цифр: 0, 1, 2, 3, 4?