§6. Повторные независимые испытания.

На практике часто приходится сталкиваться с задачами, которые можно представить в виде многократно повторяющихся испытаний при данном комплексе условий, в которых представляет интерес вероятность числа m наступлений некоторого события А в n испытаниях. Если вероятность наступления события А в каждом испытании не меняется в зависимости от исходов других, то такие испытания называются независимыми относительно события А. Если независимые повторные испытания проводятся при одном и том же комплексе условий, то вероятность наступления события А в каждом испытании одна и та же. Такая последовательность независимых испытаний получила название схемы Бернулли (Якоб Бернулли швейцарский математик 1654 – 1705).

Формула Бернулли.

Теорема. Если вероятность p наступления события А в каждом испытании постоянна, то вероятность 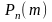того, что событие А наступит m раз в n независимых испытаниях, равна

, где q=1-p

(доказательство самостоятельно)

Следствия:

1. (вероятность того, что событие А не произойдет ни разу).

2. (вероятность того, что событие А произойдет n раз).

3. (вероятность того, что событие А произойдет только один раз).

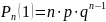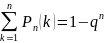4. (вероятность того, что событие А произойдет хотя бы один раз).

Наивероятнейшее число

Число наступления события А в n независимых испытаниях называется наивероятнейшим, если по крайней мере не меньше вероятности других событий 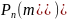при любом m, то есть

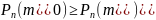
Можно показать, что:

Пример:

Вероятность изготовления на автоматическом станке стандартной детали равна 0,8. Найти наивероятнейшее число появления бракованных деталей из 5 отобранных и вероятность этого числа.

Пусть событие А- изготовление бракованной детали.

P(A)=1-0,8=0,2=p, q=0,8, n=5

5∙0,2-0,8≤ 5∙0,2+0,2 0,2≤ 1,2 =>

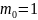
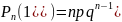
Замечание:

Если m и n велики, p мало, то вычисление по формуле Бернулли будет затруднительно. В этом случае применяют приближенные, так называемые асимптотические формулы.

Формула Пуассона.

(Пуассон Симеон Дени французский математик 1781-1840)

Если вероятность p наступления события А в каждом испытании стремится к нулю (p→0) при неограниченном увеличении числа испытаний (n→∞), причем произведение np стремится к постоянному числу λ (np→λ), то вероятность того, что событие А появится m раз в n независимых испытаниях, приближенно равна:

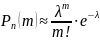, где λ=np

Функция - функция Пуассона. Для нахождения значений этой функции существуют специальные таблицы для различных m и λ.

Замечание: формула Пуассона применяется, когда npq≤10.

Пример:

На факультете насчитывается 1825 студентов. Какова вероятность того, что 1сентября является днем рождения четверых студентов?

n=1825 , m=4 , p=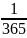 , λ=np=1825∙

Применим приближенную формулу Пуассона:

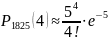
0.1755 (нашли по таблице)

Локальная формула Муавра – Лапласа.

(Муавр Абрахам де английский математик, француз по национальности, 1667-1754; Лаплас Пьер Симон французский математик 1749-1827; формулы получены Муавром в 1718г. для p= q= , общий случай рассмотрен Лапласом в 1812г.)

Если m и n велики, но число m-np ограничено, npq ≥10, то применяем приближенную формулу для вычисления вероятности появления события А m раз в n независимых испытаниях:

,

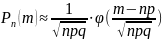где

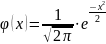
Для упрощения расчетов составлена таблица значений функции . Пользуясь этой таблицей, необходимо учитывать свойства функции

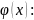
1. - четная функция = ;

2. .

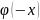Пример:

Имеется партия резисторов из 10000 штук. Какова вероятность того, что в этой партии бракованных резисторов 20 штук, если вероятность брака 0,001.

n=10000 , m=20, p=0,001 , q=1-p=0,999

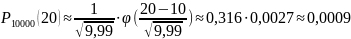
Замечание:

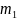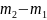Иногда требуется найти вероятность наступления события А в n испытаниях от до раз. Если разность не велика, то можно воспользоваться предыдущими формулами и применить теорему сложения.

Если разность значительная, то указанные формулы приводят к затруднительному решению. В этом случае используют интегральную формулу Муавра – Лапласа.