Складовий критерій

Cкладовий критерій складається з двох критеріїв.

Критерій 1

Відповідно до першого критерію необхідно знайти зміщену оцінку середнього квадратичного відхилення:

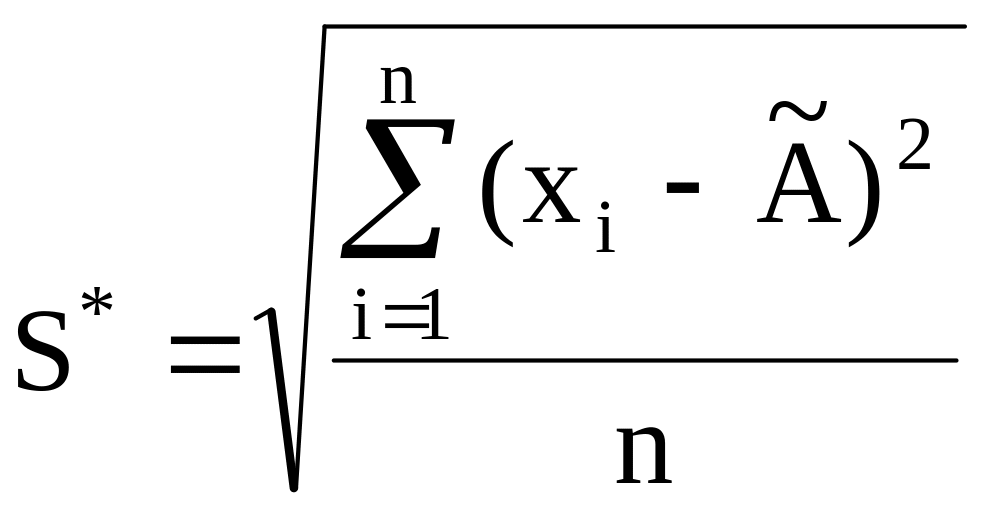, (16)

де - зміщена оцінка середнього квадратичного відхилення; - результат вимірювання; - кількість результатів вимірювань.

Після чого слід порахувати відношення :

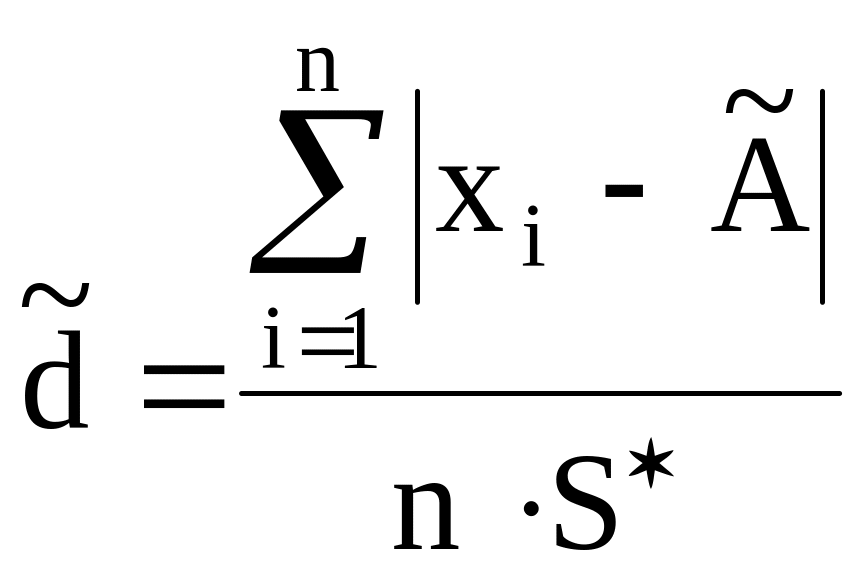. (17)

Результати групи спостережень вважаються розподіленими нормально, якщо виконується умова:

, (18)

де і – квантілі розподілу, які визначають з таблиці 3 додатку 3 залежно від n , і (для технічних вимірювань обираємо =0.05 або 5%, =0.95 або 95%)

Критерій 2

Можна вважати, що результати спостережень належать до нормального розподілу, якщо не більше m різниць перевищують значення добутку

, (19)

де S – незміщена оцінка середнього квадратичного відхилення, що визначається за формулою (4); – верхня квантіль розподілу нормованої функції Лапласа, яка відповідає ймовірності P/2, її знаходять із таблиці 5 у додатку 3.

Значення ймовірності P визначають з таблиці 4 у додатку 2 за вибраним рівнем значення q₂ (для технічних вимірювань q₂=5%) і числом результатів спостережень n.

Якщо для критерію 1 вибраний рівень значення q₁, а для критерію 2 – рівень значення q₂ , то результуючий рівень значення складеного критерію .

Якщо виконуються умови обох критеріїв, то розподіл результатів спостережень відповідає нормальному закону розподілу. Якщо хоча б один з критеріїв не виконується, то розподіл результатів спостережень не відповідає нормальному закону розподілу.

Методика Пірсона

Для того, щоб перевірити з допомогою методики Пірсона, чи результати вимірювань належать до нормального розподілу, додатково необхідно вирахувати дисперсії характеристик асиметрії та ексцесу які залежать лише від числа спостережень n і відповідно визначають за формулами:

; (20)

(21)

і перевірити виконання наступних умов:

(22)

та (23)

де – показник асиметрії; – дисперсія характеристики асиметрії; – показник ексцесу; D(b₂) – дисперсія характеристики ексцесу.

Якщо ці умови виконуються, то студент робить висновок, що розподіл результатів спостережень відповідає нормальному закону розподілу і навпаки.

Випадкову складову похибки результату вимірювання визначають за формулою:

, (24)

де – оцінка середньоквадратичного відхилення результату вимірювань, вирахувана за формулою (12); t – коефіцієнт Ст’юдента, який знаходять шляхом інтерполяції з таблиці 6 у додатку 3 для заданих числа f=n-1 ступеня вільності та довірчої ймовірності P_д =95%.

2.2. Розрахунок довірчої межі невиключеної систематичної похибки результату вимірювання

Невиключена систематична похибка результату вимірювання складається зі складових невиключених систематичних похибок методу, засобів вимірювань і їх похибок, викликаних іншими джерелами. Якщо випадкові складові похибки засобів вимірювань знехтувано малі, то границями складових невиключеної систематичної похибки є, наприклад, границі їх допустимих основних і додаткових похибок .

Для визначення невиключеної систематичної похибки результату вимірювання попередньо необхідно проаналізувати умови проведення вимірювань і визначити, які величини крім вхідної відповідно до заданої математичної моделі ПВП впливають на вихідну, а також розміри можливих відхилень від початкових значень цих, так званих неінформативних параметрів. На базі математичної моделі (відповідно до завдання) вираховують зміни вихідного сигналу ПВП, як правило, при одному з крайніх значень діапазону вимірювання (де найбільший вихідний сигнал), викликані почерговими змінами кожного з неінформативних параметрів від нормальних значень. Ці зміни вихідного сигналу ПВП можна вважати складовими невиключених залишків систематичної похибки, які застосовуються для вирахування систематичної похибки ПВП.

Складові невиключеної систематичної похибки результату вимірювання сумують, при цьому невиключені систематичні похибки засобів вимірювань кожного типу і похибки поправок розглядають як випадкові величини. Якщо розподіл цих випадкових величин невідомий, то їх розподіл приймають за рівномірний.

Межі невиключеної систематичної похибки результату вимірювання при рівномірному розподілі невиключених систематичних похибок засобів вимірювань, методу та похибок, викликаних іншими джерелами, визначають за формулою:

, (25)

де – границя i-ї невиключеної систематичної похибки; k – коефіцієнт , що визначається прийнятою довірчою ймовірністю; m - число похибок, що сумуються.

Коефіцієнт k вибирається рівним: 1,1- при довірчій ймовірності P=0,95; 1,4 – при P=0,99 і m>4; за графіком залежності k=f(m,l) (рис.1) при m 4.

Довірчу ймовірність для обчислення границь невизначеної систематичної похибки приймають такою ж самою, як й при обчисленні довірчих меж випадкової похибки результату вимірювання .

Рис.1 Графік залежності k=f(m,l):

1 – m = 2 ;

2 – m = 3 ;

3 – m = 4.