Лекция №8. Временные ряды и прогнозирование

ПЛАН

8.1. Краткие теоретические сведения

8.2. Выявление сезонной составляющей тренда

8.3. Экспоненциальное сглаживание

8.1. Краткие теоретические сведения

При построении классической модели регрессии характер экспериментальных данных, как правило, не имеет принципиального значения. Однако это оказывается не так, если условия Гаусса-Маркова нарушены. В отличие от пространственных выборок, временные данные, как правило, нельзя считать независимыми.

Под временным рядом в экономике понимают набор данных, представляющих результаты наблюдения за какой-либо случайной величиной в последовательные моменты времени.

Если проанализировать временной ряд, то можно обнаружить определенные закономерности. Например, на графике, отражающем значения экономических показателей за несколько лет, можно обнаружить определенную тенденцию (тренд); а на графике, представляющем значение показателей за более короткие периоды времени (неделя, месяц, квартал), можно обнаружить эффект сезонных колебаний.

Трендом называют общую тенденцию (закономерность) изменения наблюдаемого параметра во времени. В бизнесе тренд дает количественное представление о направлениях развития секторов рынка, ценах, объемах продаж и др. показателей. Для выявления тренда используют статистические методы, которые позволяют устранить эффект сезонных колебаний.

Чаще всего для выявления тренда применяют метод наименьших квадратов (МНК), а также метод скользящих средних.

Пример 8.1. Рассмотрим данные об объемах продаж определенного продукта, в которых проявляется сезонный характер изменений. В связи с сезонным характером спроса на данный продукт объем продаж растет не постоянно. Каждый год рост объемов продаж в первом и втором кварталах сменяется спадом в третьем квартале (табл. 8.1)

Таблица 8.1.

Данные об изменениях объемов продаж

Квартал	Годы
	1989	1990	1991
1 2 3 4	100 130 115 130	130 160 145 160	160 190 175 190

Предположим, что все предпосылки МНК выполняются,и тренд является линейной функцией времени. Оценим тренд по МНК.

Решение. Будем использовать формулы:

,

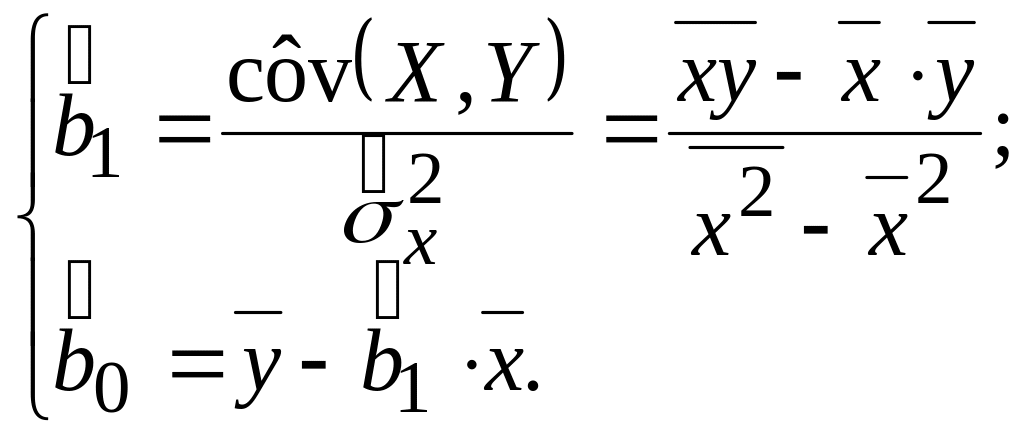в которых значения объясняющей переменной X образуют натуральный ряд чисел от 1 до 12.

Результаты оценивания тренда с помощью функции ЛИНЕЙН имеют вид:

.

Можно заметить, что все коэффициенты тренда являются статистически значимыми. Легко также проверить по F-критерию, что качество построенного тренда можно считать высоким.

Визуализация полученного решения имеет вид:

Замечание. Следует помнить, что для наблюдений во временных рядах третье и четвертое условия Гаусса-Маркова зачастую не выполняются. Поэтому МНК нужно использовать с осторожностью, так как он может дать статистически ненадежные оценки для коэффициентов тренда. В такой ситуации проще всего использовать метод скользящих средних.

Выявление тренда по методу скользящих средних

Пример 8.2. Для исходных данных примера 8.1 выявить тренд по методу скользящих средних с интервалом сглаживания в 4 месяца.

Решение. В табл. 8.2 представлены все вычисления, необходимые для определения тренда по методу скользящих средних с интервалом сглаживания в 4 месяца. Для выявления тренда подсчитаем для каждого квартала сумму значений показателя за предшествующие четыре квартала. Далее определим значение тренда для каждого момента времени как среднее значение из двух средних величин, подсчитанных для двух периодов по четыре месяца, следующих непосредственно друг за другом.

Таблица 8.2.

Расчет значений тренда

Год	Квартал	Наблюдаемые значения (исходные данные)	Накопленные суммы за четыре предшествующих квартала		Средние значения за четыре предшествующих квартала	Значение тренда
1989	1	100
	2	130	475		118,75
	3	115	505		: 126,25	122,5=(118,75+126,25)/2
	4	130	535		: 133,75	130=(133,75+126,25)/2
1990	1	130	565		141,25	137,5=(133,75+141,25)/2
	2	160	595		148,75	145=(148,75+141,25)/2
	3	145	625		156,25	152,5=(148,75+156,25)/2
	4	160	655		163,75	160=(163,75+156,25)/2
1991	1	160	685		171,25	167,5=(163,75+171,25)/2
	2	190	715		178,75	175=(178,75+171,25)/2
	3	175
	4	190