Индивидуальное задание № 7

Дан куб АВСDА₁В₁С₁D₁ с ребром, равным а, Р – точка пересечения диагоналей куба (центр куба), О и О₁ – центры нижнего и верхнего оснований соответственно. Найдите расстояние между точками М и N, если:

1. М  АО₁, АМ : АО₁ = 2 : 3; N  РС, РN : РС = 1 : 4.

2. М  DВ₁, DМ : DВ₁ = 1 : 2; N  D₁С, D₁N : D₁С = 1 : 3.

3. М  АО₁, АМ : АО₁ = 2 : 3; N  ОС, ОN : ОС = 1 : 2.

4. М  DР, DМ : DР = 1 : 3; N  В₁С, В₁N : В₁С = 2 : 3.

5. М  А₁О₁, А₁М : А₁О₁ = 2 : 3; N  СР, СN : СР = 1 : 4.

6. М  ВD₁, ВМ : ВD₁ = 1 : 4; N  О₁С, О₁N : О₁С = 1 : 2.

7. М  А₁С, А₁М : А₁С = 1 : 3; N  С₁D, С₁N : С₁D = 2 : 3.

8. М  О₁В₁, О₁М : О₁В₁ = 3 : 4; N  А₁С, А₁N : А₁С = 2 : 3.

9. М  СА₁, СМ : СА₁ = 1 : 5; N  ВD, ВN : ВD = 1 : 2.

10. М  СР, СМ : СР = 1 : 2; N  ВО₁, ВN : ВО₁ = 1 : 4.

11. М  DА₁, DМ : DА₁ = 3 : 4; N  В₁С, В₁N : В₁С = 1 : 2.

12. М  ОD, ОМ : ОD = 1 : 3; N  ВС₁, ВN : ВС₁ = 4 : 5.

13. М  ВО, ВМ : ВО = 2 : 3; N  А₁С, А₁N : А₁С = 1 : 5.

14. М  А₁D, А₁М : А₁D = 4 : 5; N  ОС₁, ОN : ОС₁ = 1 : 2.

15. М  DС₁, DМ : DС₁ = 3 : 5; N  А₁С₁, А₁N : А₁С₁ = 1 : 3.

16. М  DО₁, DМ : DО₁ = 2 : 5; N  С₁О, С₁N : С₁О = 1 : 2.

17. М  ВР, РМ : ВР = 2 : 3; N  СА₁, СN : СА₁ = 2 : 5.

18. М  АР, АМ : АР = 1 : 3; N  СО₁, СN : СО₁ = 2 : 5.

19. М  РВ, РМ : РВ = 3 : 4; N  СD₁, СN : СD₁ = 1 : 2.

20. М  DВ₁, DМ : DВ₁ = 2 : 5; N  СР, СN : СР = 1 : 4.

21. М  ОВ₁, ОМ : ОВ₁ = 1 : 5; N  О₁С, О₁N : О₁С = 3 : 4.

22. М  А₁С, А₁М : А₁С = 2 : 3; N  ОD₁, ОN : ОD₁ = 4 : 5.

23. М  А₁Р, А₁М : А₁Р = 1 : 3; N  ВС₁, ВN : ВС₁ = 2 : 5.

24. М  ВD, ВМ : ВD = 1 : 4; N  DС, DN : DС = 2 : 3.

25. М  В₁D₁, В₁М : В₁D₁ = 2 : 5; N  РС, РN : РС = 1 : 2.

26. М  А₁Р, А₁М : А₁Р = 3 : 4; N  DС, DN : DС = 2 : 3.

27. М  АО₁, АМ : АО₁ = 1 : 3; N  В₁С, В₁N : В₁С = 4 : 5.

28. М  D₁В, D₁М : D₁В = 3 : 5; N  DС₁, DN : DС₁ = 1 : 2.

29. М  РА₁, АМ : РА₁ = 2 : 5; N  ОС, ОN : ОС = 1 : 3.

30. М  А₁D, А₁М : А₁D = 1 : 4; N  ВО₁, ВN : ВО₁ = 2 : 3.

Вариант 31

М  РD, DМ : РD = 3 : 7; N  СD₁, СN : СD₁ = 4 : 5.

Р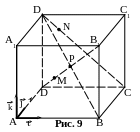 ешение. Выберем прямоугольную систему координат А  j k, где вектор  сонаправлен с вектором АВ, j - с АД и k - с АА₁ (рис. 9).

Найдем координаты точек D, В1, С, D1 и середины Р отрезка В1D: D(0; а; 0), В1(а; 0; а), С(а; а; 0), D1(0; а; а), Р , т.е. Р . Н айдем отношение , в котором точка М делит направленный отрезок РD: так как РМ : МD = 4 : 3 и М лежит между Р и D, то РМ = МD, откуда  = .

А налогично находим отношение , в котором точка N делит направленный отрезок СD₁: так как СN : ND₁ = 4 : 1 и N лежит между С и D₁, то СN = 4ND₁, откуда  = 4. По формулам деления отрезка в данном отношении находим координаты точек М и N :

Далее применяем формулу расстояния между двумя точками в координатах:

Ответ: MN =