Вариант 31
DC
+ OD1
CC1
OP.
Решение. Существует несколько способов решения этой задачи. Рассмотрим два из них.
I способ: заменяя в данном выражении некоторые векторы на равные им, расположим их последовательно так, чтобы начало следующего совпадало с концом предыдущего. Для этого придется воспользоваться свойствами сложения векторов и правилами треугольника или многоугольника.
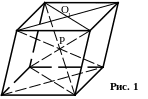
СС1 = DD1 (рис. 1) СС1 = D1D. Обозначим искомый вектор через x. Тогда х = DC + OD1 CC1 OP = DC + + OD1 + D1D OP = (OD1 + D1D + DC) OP = OC OP = PC. Ответ: РС искомый вектор.
|
D1 C1
A1 B1
D C О A B |
I
I
способ:
воспользуемся свойствами сложения
векторов и правилами сложения и вычитания
двух векторов: х
= DC
+ OD1
CC1
OP
= (DC
+ C1C)
+ + (OD1
OP)
= (DC +
D1D)
+
PD1
= (D1D
+ DC)
+ PD1
= D1C
+ PD1
= PD1
+ + D1C
= PC.
Ответ: РС - искомый вектор.
Замечание 1. В ответе вместо вектора РС может получиться другой равный ему вектор, например, А1Р.
Замечание 2. Индивидуальное задание №1 достаточно выполнить одним способом, выбрав наиболее рациональный.
Индивидуальное задание № 2
AA1, BB1 и СС1 - медианы треугольника АВС, М - их точка пересечения. Найдите координаты вектора р в базисе е1, е2, если:
|
|