
- •Оглавление
- •Введение
- •§1. Элементы векторной алгебры на плоскости и в пространстве Индивидуальное задание № 1
- •Вариант 31
- •Индивидуальное задание № 2
- •Вариант 31
- •Индивидуальное задание № 3
- •Вариант 31
- •§2. Метод координат на плоскости и в пространстве. Векторное и смешанное произведения векторов Индивидуальное задание № 4
- •Вариант 31
- •Индивидуальное задание № 5
- •Вариант 31
- •Индивидуальное задание № 6
- •Вариант 31
- •Индивидуальное задание № 7
- •Вариант 31
- •Индивидуальное задание № 8
- •Вариант 31
- •Индивидуальное задание № 9
- •Вариант 31
- •Индивидуальное задание № 10
- •Вариант 31
- •Индивидуальное задание № 11
- •Вариант № 31
- •Индивидуальное задание № 12
- •Вариант 31
- •§3. Прямая линия на плоскости. Прямые и плоскости в пространстве Индивидуальное задание № 13
- •Вариант 31
- •Индивидуальное задание № 14
- •Вариант 31
- •Индивидуальное задание № 15
- •Вариант 31
- •Индивидуальное задание № 16
- •Вариант 31
- •Индивидуальное задание № 17
- •Вариант 31
- •§4. Линии второго порядка на плоскости Индивидуальное задание № 18
- •Вариант 31
- •Индивидуальное задание № 19
- •Вариант 31
- •Индивидуальное задание № 20
- •Вариант 31
- •Индивидуальное задание № 21
- •Вариант 31
- •§5. Поверхности второго порядка Индивидуальное задание № 22
- •Вариант 31
- •Индивидуальное задание № 23
- •Вариант 31
- •Индивидуальное задание № 24
- •Вариант 31
- •Индивидуальное задание № 25
- •Вариант 31
- •Рекомендуемая литература Основная
- •Дополнительная
Индивидуальное задание № 21
Приведите общее уравнение линии второго порядка к каноническому виду и изобразите данную линию:
x2 – 6xy + 9y2 8
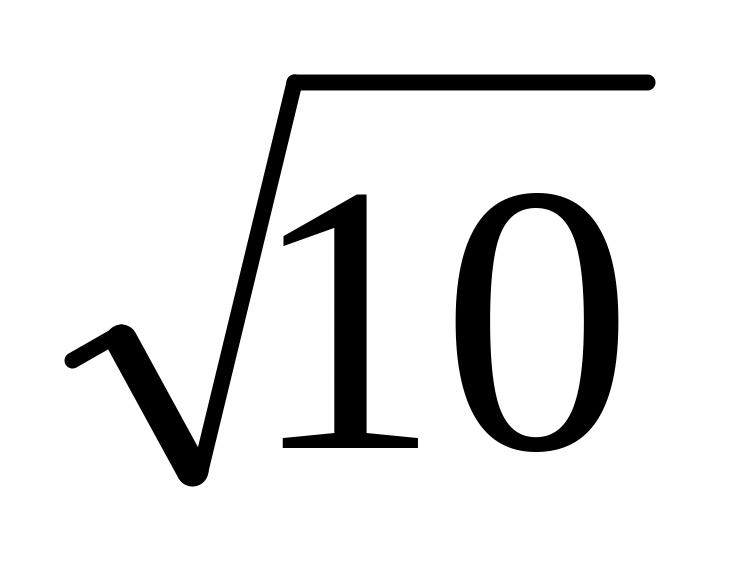 x
+ 4
y
+ 7 = 0.
x
+ 4
y
+ 7 = 0.3x2 + 4xy
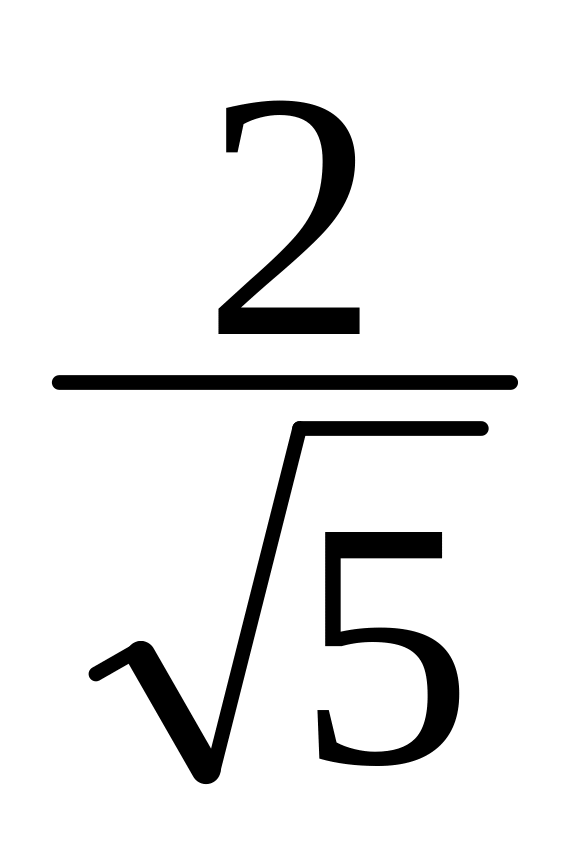 x
+
x
+
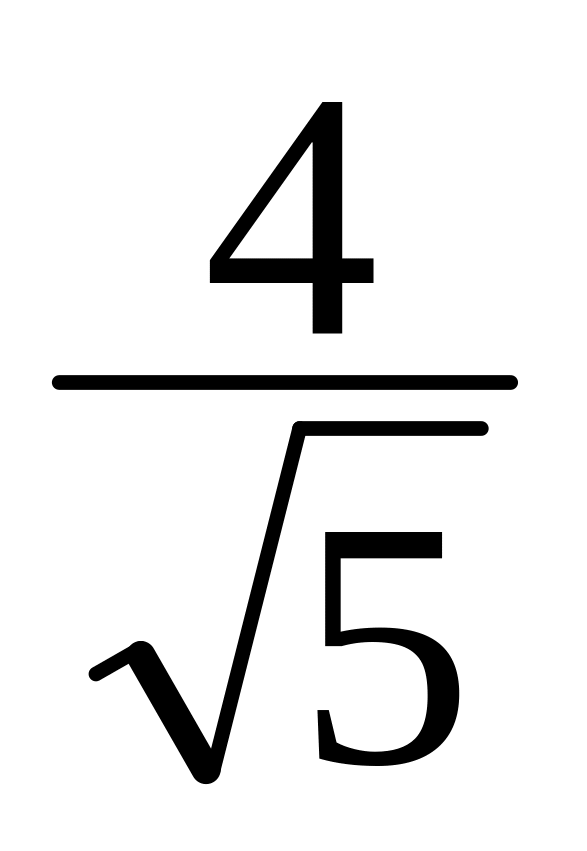 y
+ 3 = 0.
y
+ 3 = 0.x2 – 4xy + 4y2 50x 75 = 0.
6xy + 8y2 + x + 3 y +
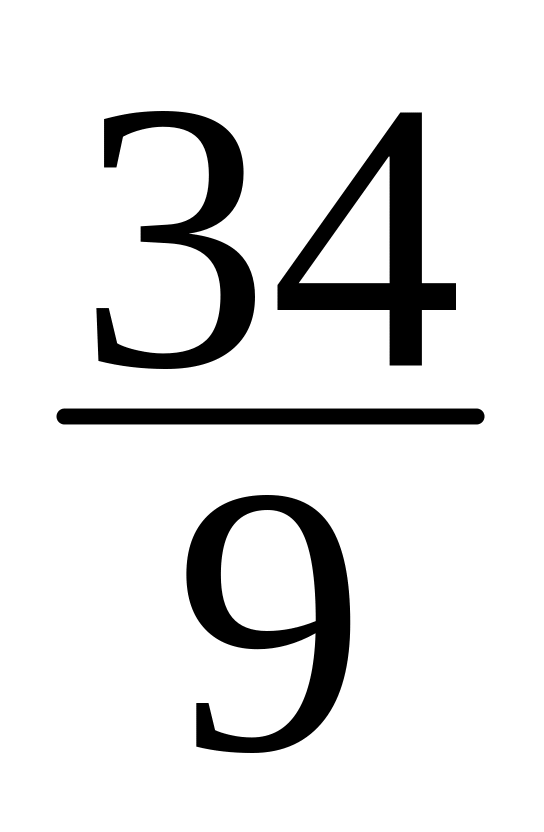 = 0.
= 0.4x2 – 4xy + y2 2x 14y + 7 = 0.
x2 – 2xy + y2 8x 8y 16
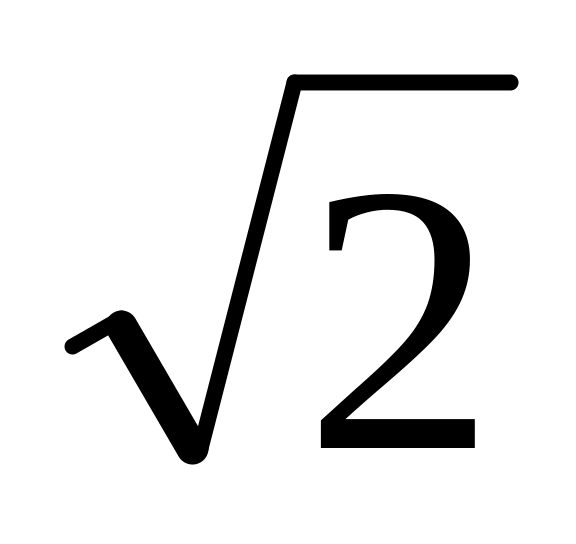 = 0.
= 0.xy + 2x + y +
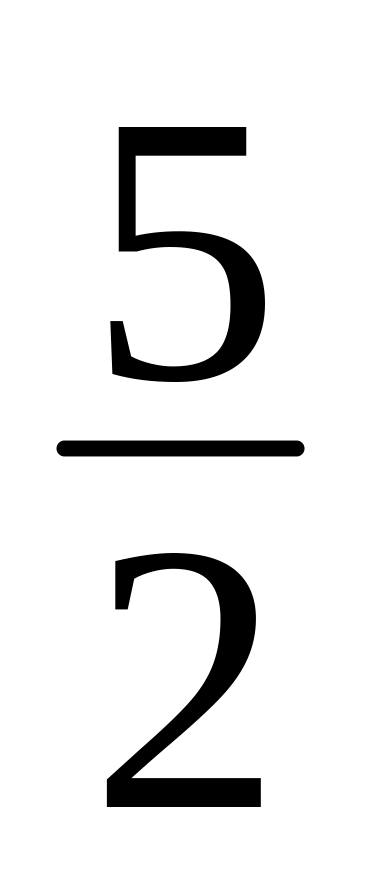 = 0.
= 0.x2 – 2xy + y2 10x 6y + 25 = 0.
3x2 + 10xy + 3y2 2x 14y 13 = 0.
4xy + 3y2 + 16x + 12y 36 = 0.
9x2 – 6xy + y2 3 x 9 y 90 = 0.
x2 + xy + y2 + x + y = 0.
xy + 4x + 4y = 0.
10x2 + 6xy + 2y2 2x + 4y 3 = 0.
4x2 – 4xy + y2 x 2 = 0.
x2 + 6xy + 9y2 + 20x + 10y
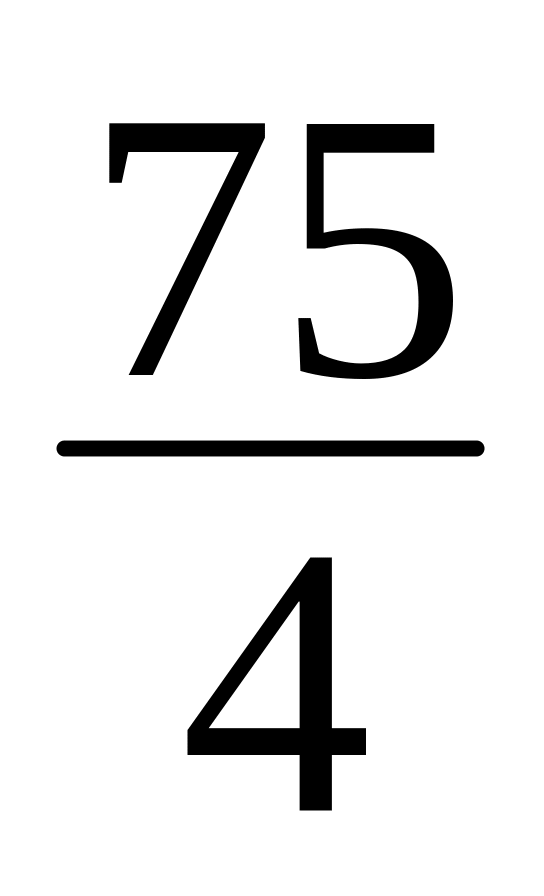 = 0.
= 0.3x2 + 4xy + 2x + y + 1 = 0.
5x2 + 6xy + 5y2 16x 16y 16 = 0.
4xy + 3y2 + 8x + 16y + 24 = 0.
4x2 – 4xy + y2 4x 4y + 7 = 0.
x2 – 2xy + y2 6x 6y 6 = 0.
4xy + 3y2 16x + 8y 64 = 0.
x2 – 6xy + 9y2 20x 11 = 0.
6xy + 8y2 + x + 3y +
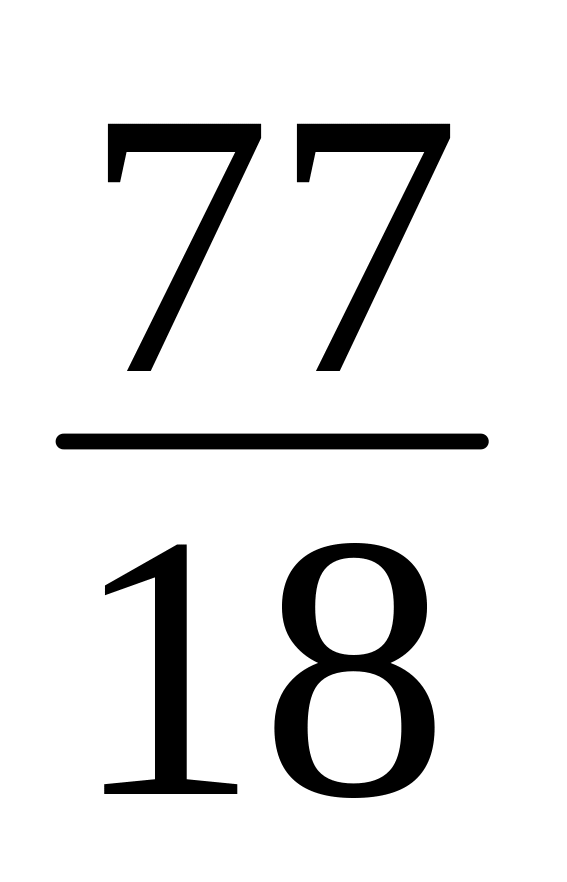 = 0.
= 0.x2 – 4xy + 4y2 5x + 6 = 0.
5x2 + 12xy 22x 12y 19 = 0.
9x2 – 6xy + y2 4 x 12 y 8 = 0.
x2 – 6xy + 9y2 + 30y
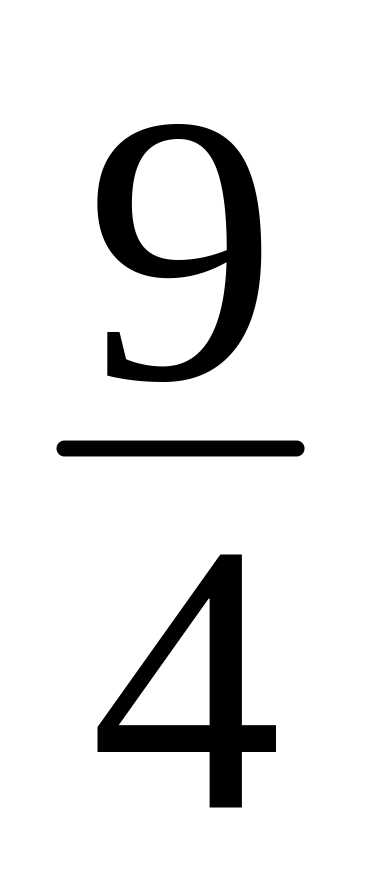 = 0.
= 0.x2 – 2xy + y2 6x 6y 3 = 0.
5x2 + 8xy + 5y2 18x 18y + 9 = 0.
Вариант 31
9x2 – 6xy + y2 + 20 x + 10 = 0.
Р ешение.
I. Выполним поворот
координатных векторов i
и j системы координат
О i
j, в которой дано общее
уравнение линии. Для этого найдем угол
поворота :
ешение.
I. Выполним поворот
координатных векторов i
и j системы координат
О i
j, в которой дано общее
уравнение линии. Для этого найдем угол
поворота :
ctg2
=
 ;
cos2
=
;
cos2
=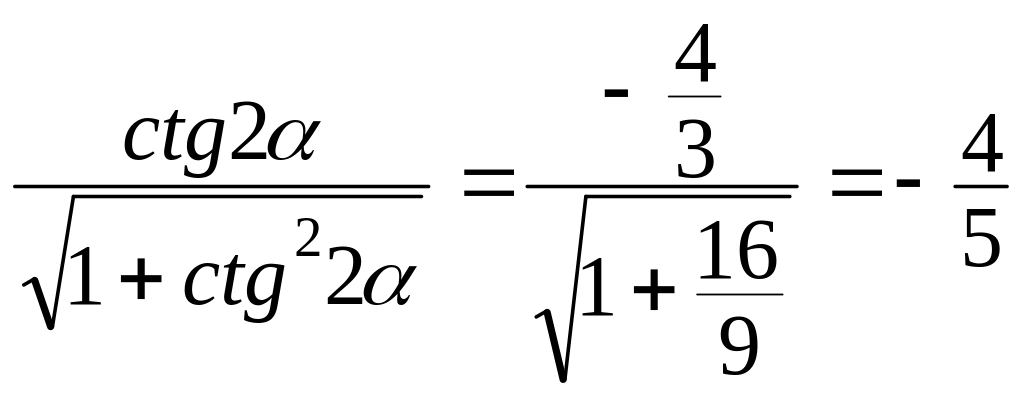 ;
sin =
;
sin =![]()
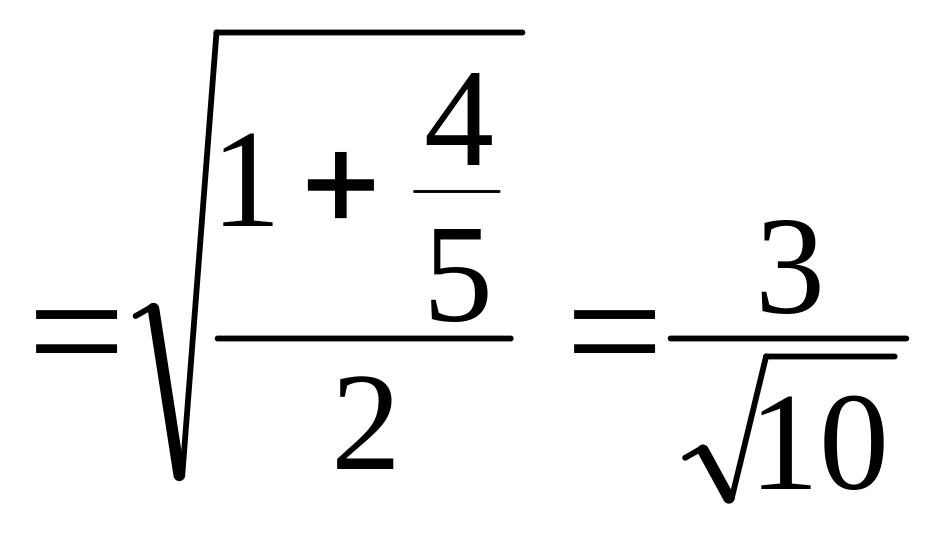
 ;
cos
=
;
cos
=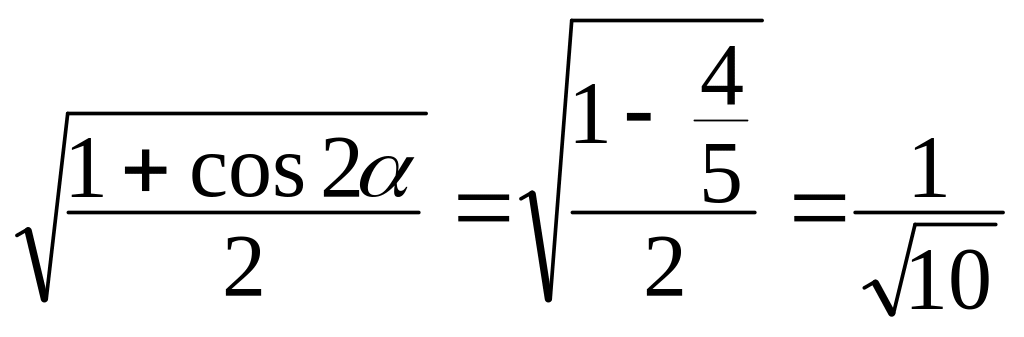 .
Тогда i / =
(
.
Тогда i / =
(![]() ),
j / =
(
),
j / =
(![]() ),
а формулы поворота координатных
векторов имеют вид:
),
а формулы поворота координатных
векторов имеют вид:
![]()
Н
айдем
уравнение данной линии в системе
координат О
i
/
j
/
(Ox/y/),
полученной из системы О
i j
(Оху) поворотом координатных
векторов на угол :
![]()
![]() Раскрыв скобки и приведя подобные члены,
получим:
Раскрыв скобки и приведя подобные члены,
получим:
![]() .
.
I I.
Выполним перенос начала координат О
системы О
i
/
j
/
(Ox/y/).
Для этого выделим полный квадрат при
у/
и освободимся от свободного члена:
I.
Выполним перенос начала координат О
системы О
i
/
j
/
(Ox/y/).
Для этого выделим полный квадрат при
у/
и освободимся от свободного члена:
![]()
![]() Положим Х =
Положим Х =
![]() ,
Y =
,
Y =
![]() .
Тогда формулы переноса начала имеют
вид:
.
Тогда формулы переноса начала имеют
вид:
![]()
Т очка О перейдет в точку О/(4; 3) (координаты точки О/ даны в системе координат О i / j / (Ox/y/)).
В системе координат О/ i / j / (О / ХY) уравнение данной линии таково:
Y 2 + 2X = 0, т.е. Y 2 = 2X.
Следовательно, линия, данная в задаче, является параболой с осью О/Х и вершиной О/.
Для построения
параболы используем вспомогательные
точки: М1(![]() ;1);
М1/(
;
1); М2 (2;
2); М2/ (2;
2).
;1);
М1/(
;
1); М2 (2;
2); М2/ (2;
2).
С троим сначала систему координат О i j (Оху) (рис. 25), затем О i / j / (Ox/y/) и, наконец, О/ i / j / (О / ХY). В системе О/ i / j / строим параболу.
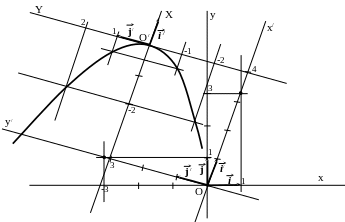
Рис. 25
