Индивидуальное задание № 14
Найдите уравнение биссектрисы внутреннего угла А треугольника АВС, если:
|
|
Вариант 31
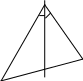
Найдите уравнение биссектрисы внутреннего угла В треугольника АВС, если А(11; 7), В(3; 0), С(9; 7).
D
|
В
С
А Рис. 18 |
,
откуда АВ: 7х + 8у – 21 = 0.
,
откуда ВС: 7х – 12у – 21 =
0.
Запишем равенство
(1) в координатах:
,
т.е.
.
(2)
Для раскрытия
модуля воспользуемся условием, что ВD
– биссектриса внутреннего угла.
Определим, какой знак имеют трехчлены
7х + 8у – 21 и 7х
– 12у – 21 в точках, лежащих внутри
угла АВС. Возьмем какую-либо точку
внутри угла АВС, например, середину
В1 стороны АС. Найдем ее
координаты: В1
,
т.е. В1(1; 7).
Определим знаки трехчленов 7х
+ 8у
21 и 7х
12у
21 в точке В1: 71
+ 8(7)
21 =
7 –
56
– 21
= 70
< 0, т.е. под модулем в левой части
уравнения (2) стоит отрицательное
число.
71 12(7) 21 = 7 + 84 – 21 = 70 > 0, т.е. под модулем в правой части уравнения (2) стоит положительное число.
Следовательно,
первый модуль раскрываем со знаком «»,
второй – со знаком «+»:
.
Раскрывая скобки и приводя подобные
члены, получим уравнение искомой
биссектрисы:
Ответ:
Индивидуальное задание № 15
Найдите длины сторон, величины углов, длины высот, уравнения прямых, содержащих стороны, медианы, биссектрисы, высоты, уравнения серединных перпендикуляров к сторонам, координаты центра тяжести, ортоцентра, центра вписанной и центра описанной окружности треугольника АВС, если:
|
|