4. Применение эквивалентных бесконечно малых
Бесконечно
малые
и
называются эквивалентными при
,
если
Обозначается эквивалентность так:
.
Применение эквивалентных б.м. является
очень эффективным способом раскрытия
неопределенностей. В основе следующая
теорема.
Теорема.
Пусть функции
и
являются эквивалентными при
.
Если существует конечный или бесконечный
,
то существует
,
причем
.
(3)
Из
этой теоремы следует, что если при
,
,
то
;
.
Эти равенства означают, что при вычислении пределов множители в числителе или в знаменателе можно заменить на эквивалентные
Приведем некоторые пары эквивалентных бесконечно малых величин
; 
;
; 
;
; 
.
Пример
1. Вычислить
.
Решение.
Функции
являются б.м. при
,
заменим их эквивалентными б.м.:
,
при
.
Тогда
.
При
помощи замены б.м. на эквивалентную
удается очень быстро преодолеть те
искусственные , иногда громоздкие
преобразования, которые нами использовались
при раскрытии неопределенностей другими
способами. Чтобы убедиться в этом,
вернемся к примеру 3, п.3 и вычислим его
с помощью эквивалентных б.м. . При
,
поэтому
;
бесконечно малая
.
Тогда
.
Преимущества использования бесконечно малых очевидны.
Пример
2. Вычислить
.
Решение.
Обозначим
и заметим, что при
новая переменная y
тоже
.
Тогда
при
,
т.е.
.
При
б.м.
.
Тогда
.
Метод замены переменной, использованный в данном примере, значительно расширяет возможности применения эквивалентных б.м. величин.
Замечание.
Не рекомендуется заменять под знаком
предела слагаемые на эквивалентные им
величины. Например, при
;
.
Если перейти к эквивалентным функциям
в примере
,
то получим
.
В действительности все обстоит по-другому:
.
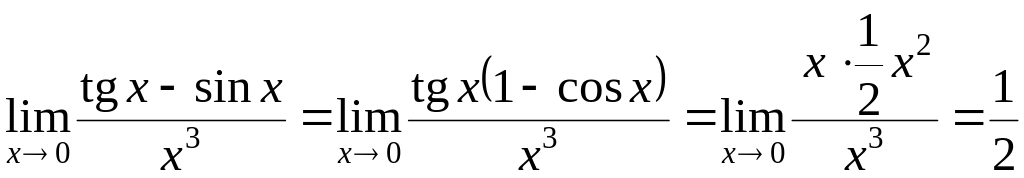Рассмотренные
примеры связаны с неопределенностью
,
но эквивалентные б.м. можно использовать
при раскрытии и других неопределенностей.
Пример
3. Вычислить
.
Решение.
Неопределенность
.
Применим следующие преобразования:
.
При
,
,
тогда
.
В свою очередь,
.
Поэтому
.
Пример
4. Вычислить
,
где
-
произвольное положительное число.
При
данный предел можно вычислить путем
умножения и деления на сопряженное
выражение. Для других значений
такой метод уже не проходит. Используя
эквивалентные б.м. этот предел можно
вычислить без особого труда. Сначала
применим дополнительные преобразования:
.
Т.к.
при
,
то
.
Тогда
.
В
зависимости от возможных значений
показателя степени функции
ведет себя по-разному при
.
Если
,
то
.
Тогда искомый предел равен 0. Если
,
то он равен
,
и наконец, если
,
то
,
предел равен
.
5. Раскрытие неопределенностей по правилу Лопиталя
Неопределенности
.
Если функции f(x)
и ф(x)
дифференцируемые в окрестности точки
a
и являются
бесконечно малыми (бесконечно большими)
при
,
то из существования предела
следует существование
,
причем
(4).
Раскрытие неопределенностей по формуле (4) называется правилом Лопиталя.
Пример
1. Вычислить
.
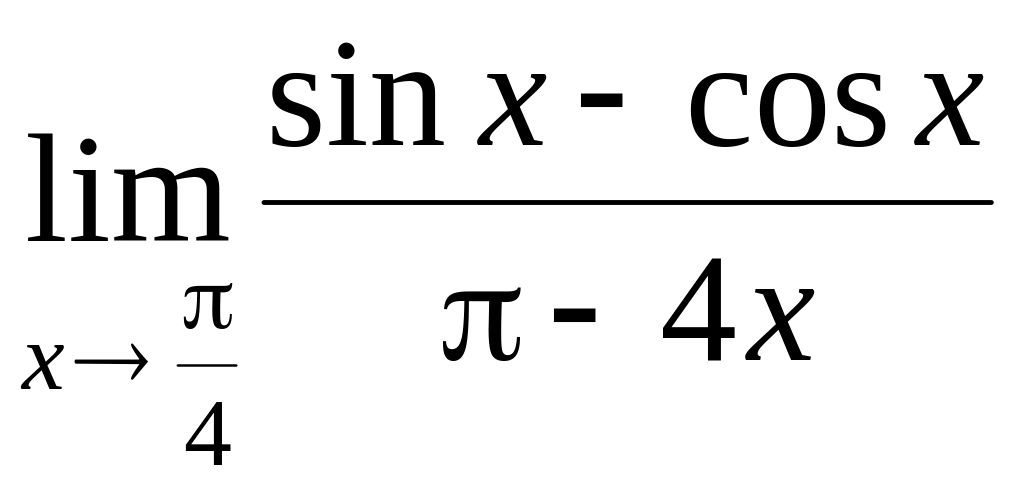Решение.
При
числитель и знаменатель дроби стремятся
к нулю, мы имеем неопределенность
.
Рассмотрим предел отношения производных:
.
По
формуле (4) данный предел тоже равен
.
Пример
2.
,
т.к.
при
.
Замечание
1. В некоторых
случаях, после применения формулы (4),
отношение производных может оказаться
неопределенностью
.
Тогда правило Лопиталя применяют еще
раз, т.е. переходят к пределу отношения
производных второго порядка.
Замечание 2. В целях сокращения вычислений рекомендуется правило Лопиталя применять в сочетании с другими приемами раскрытия неопределенностей.
Пример 3.
.
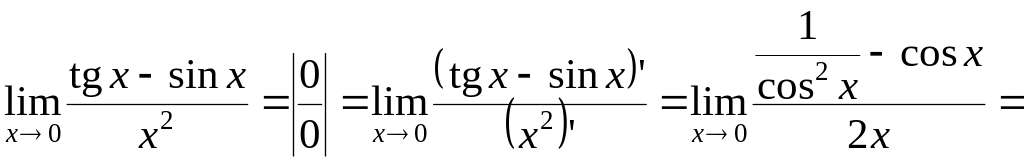
Получили предел произведения двух функций. Вычислим их отдельно. Предел второго сомножителя приводит к неопределенности . Чтобы ее раскрыть, применим правило Лопиталя повторно:
.
По теореме о пределе произведения исходный предел равен 0.
Пример
4. Вычислить
.
Применение
правила Лопиталя приводит к сложному
выражению. Проще поступить так. При
,
,
тогда
.
Тогда
.
Таким образом, в данном примере мы использовали эквивалентность б.м. и повторное применение правила Лопиталя.
Неопределенности
.
Для применения правила Лопиталя к
раскрытию этих неопределенностей путем
тождественных преобразований необходимо
их свести к неопределенности
.
Здесь можно использовать такие же
приемы, как в пункте 3.
Пример
5.
.
Решение.
Неопределенность
.
Данное выражение представим в виде
и вычислим отдельно предел показателя
степени:
.
Тогда
.
Пример
6.
Решение.
Есть неопределенность
,
т.к.
при
.
Рассмотрим логарифм данного выражения:
.
При
,
поэтому
при
.
Используя эту эквивалентность, получим
.
Тогда
.
Заключение. Мы рассмотрели некоторые приемы вычисления пределов функций одной переменной. Основное внимание при этом было уделено раскрытию неопределенностей различными методами. Существуют и другие, более тонкие методы раскрытия неопределенностей, не рассмотренные в настоящей работе. С ними вы сможете ознакомиться по книгам, список которых приведен выше.
Мы, считаем нужным отметить, что для овладения практикой вычисления пределов необходимо значительное количество упражнений. С этой целью к методическим указаниям приложены варианты контрольных работ. Задачи каждого варианта решить при следующих условиях:
1 – вычислить пределы с помощью алгебраических преобразований;
2 – вычислить пределы с помощью замечательных пределов;
3 – найти пределы, используя эквивалентные бесконечно малые;
4 – раскрыть неопределенности по правилам Лопиталя (при необходимости использовать другие приемы).