2.8. Условие совместности линейной системы уравнений

Теорема Кронекера-Капелли

А. Случай неоднородных систем

Будем исходить из системы m линейных уравнений с n неизвестными

(1)

Добавим к основной матрице А системы (1) столбец свободных членов

.

получим так называемую расширенную матрицу исходной системы.

Теорема Кронекера-Капелли.

Для того чтобы система линейных уравнений (1) была совместной необходимо и достаточно, чтобы ранг расширенной матрицы был равен рангу ее основной матрицы А, т.е.

.

Необходимость. Пусть система (1) совместна. Представим ее в виде суммы матриц-столбцов

. (2)

Данная запись означает, что столбец свободных членов является линейной комбинацией столбцов основной матрицы А с коэффициентами . Поэтому столбец свободных членов не увеличивает числа линейно независимых столбцов и .

Достаточность. Пусть , тогда базисный минор в основной матрице А является базисным и в матрице . Это означает, что столбец свободных членов является линейной комбинацией столбцов базисного минора. Коэффициенты этой комбинации есть решение системы (1).

Следствие. Система (1) несовместна тогда и только тогда, когда в ступенчатой вид расширенной матрицы входит строка - произвольное число.

Необходимость. Пусть система (1) несовместна, тогда , что возможно только при условии, если в матрицу входит строка .

Достаточность. Если строка входит в матрицу , то и система несовместна.

Пример. Выясним вопрос совместности системы

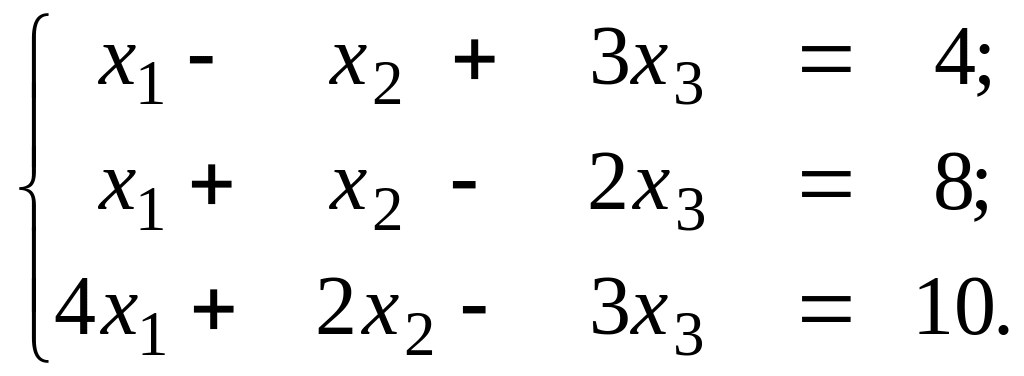
Для этого приведем расширенную матрицу системы к ступенчатому виду

Отсюда следует, что . По теореме Кронекера-Капелли система несов-местна.

Б. Случай однородных систем

Рассмотрим однородную систему линейных уравнений

(3)

Сразу заметим, что , т.е. система всегда совместна. Сразу видно, что она имеет так называемое тривиальное (нулевое) решение . Поэтому естественно поставить вопрос об условиях при которых система (3) имеет нетривиальные решения.

Теорема. Однородная система (3) имеет нетривиальные решения тогда и только тогда, когда ранг r основной матрицы системы меньше числа n ее столбцов, т.е.

.

Необходимость. Заметим, что в матричном уравнении (2) в правой части нулевая матрица, т.е. столбцы основной матрицы системы линейно зависимы с коэффициентами из которых не все равны нулю. Это означает, что порядок базисного минора r меньше числа n ее столбцов.

Достаточность. Пусть , тогда столбцы матрицы линейно зависимы с коэффициен-тами из которых хотя бы один отличен от нуля.

Следствие. Квадратная однородная линейная система имеет нетривиальные решения тогда и только тогда, когда ее определитель равен нулю.

В случае квадратной однородной системы в (3) имеем и , тогда и только тогда, когда .